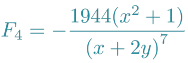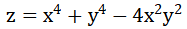本博文源于matlab求解多元函数导数。涉及求一阶/求多阶/求向量偏导数/求隐函数导数

多元函数的偏导数

diff(f(x,y,z),变量名)

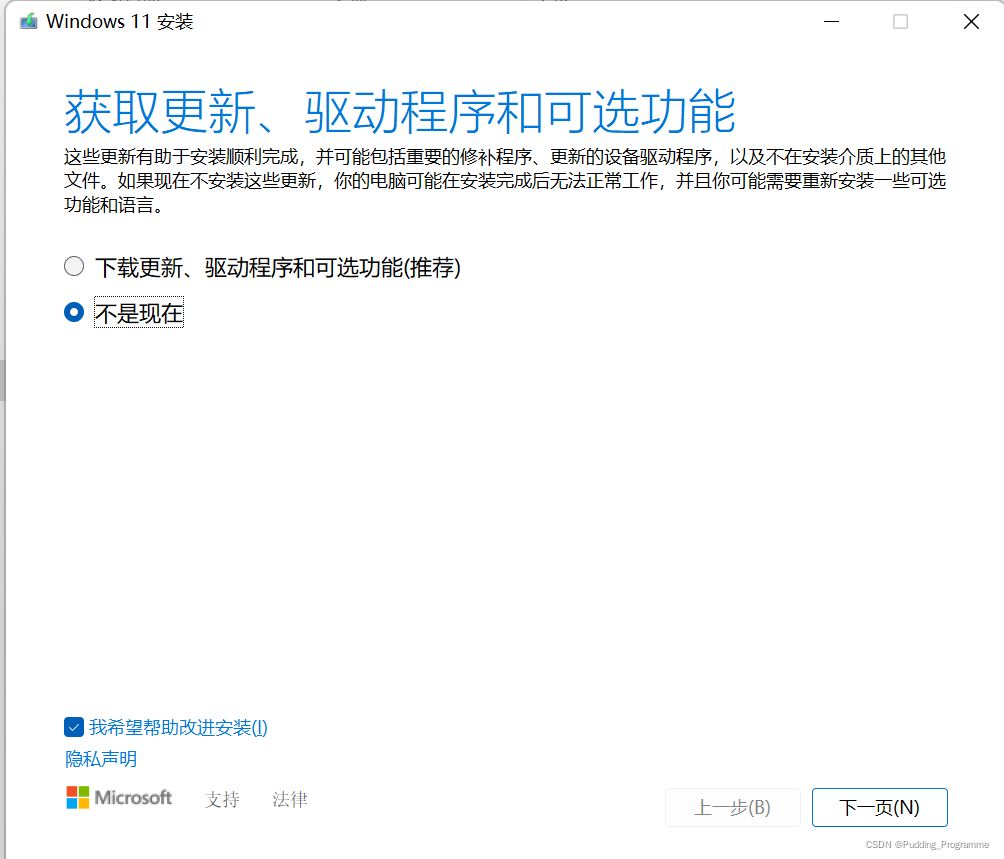
例子 求x^2+lny+根号z的偏导数

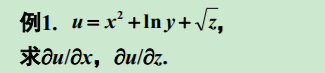
>> syms x
>> syms y
>> syms z
>> du_dx = diff(x^2+log(y)+sqrt(z),x)du_dx =2*x>> du_dz = diff(x^2+log(y)+sqrt(z),z)du_dz =1/2/z^(1/2)>> 

求高阶偏导数

diff(f(x,y,z),变量名,n)

例子：将上面的函数求4阶

>> du_dz = diff(x^2+log(y)+sqrt(z),z,4)du_dz =-15/16/z^(7/2)

求多元向量函数的偏导数

利用Jacobian矩阵求解

jacobian([f,g,h],[x,y,z]).

例子：求u的向量偏导数

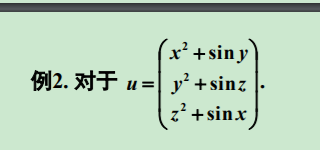
syms x y z;
>> jacobian([x^2+sin(y),y^2+sin(z),z^2+sin(x)],[x,y,z])ans =[    2*x, cos(y),      0]
[      0,    2*y, cos(z)]
[ cos(x),      0,    2*z]>> 

求隐函数形式偏导数

例子1：求dy/dz

>> syms x y
>> F=x^2*exp(-2*y)-5;
>> dy_dx=-diff(F,x)/diff(F,y)dy_dx =1/x>> 

例子：求偏导数

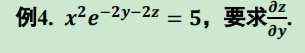
>> syms x y
>> F=x^2*exp(-2*y-2*z)-5;
>> dz_dy=-diff(F,y)/diff(F,z)dz_dy =-1>>