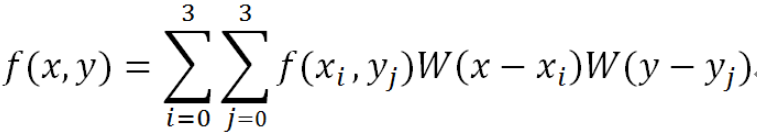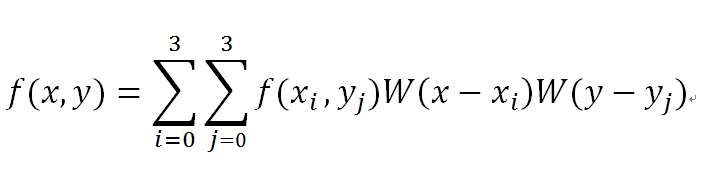在上篇文章中,我们讲解了常见的最邻近插值算法、双线性插值算法和双三次插值算法的原理与实现,三种插值算法中双三次插值算法的插值效果最好,但其也是三种算法中计算复杂度最高、耗时最长的算法。本文在给出双三次插值C++代码的基础上,着重讲解如何使用SSE指令来优化该算法,并使用双三次插值来实现图像的缩放,比较SSE指令优化前后的耗时。
1. 基于C++与Opencv的代码实现
算法原理在上篇文章中已经讲了,此处直接贴出代码:
float cubic_w_f(float x, float a)
{if (x <= 1){return 1 - (a + 3)*x*x + (a + 2)*x*x*x;}else if (x < 2){return -4 * a + 8 * a*x - 5 * a*x*x + a*x*x*x;}return 0.0;
}void cal_cubic_coeff(float x, float y, float *coeff)
{float u = x - floor(x);float v = y - floor(y);u += 1;v += 1;float a = -0.15;float A[4];A[0] = cubic_w_f(abs(u), a);A[1] = cubic_w_f(abs(u - 1), a);A[2] = cubic_w_f(abs(u - 2), a);A[3] = cubic_w_f(abs(u - 3), a);for (int s = 0; s < 4; s++){float C = cubic_w_f(abs(v - s), a);coeff[s * 4] = A[0] * C;coeff[s * 4 + 1] = A[1] * C;coeff[s * 4 + 2] = A[2] * C;coeff[s * 4 + 3] = A[3] * C;}}uchar cubic_inner(Mat src, float x_float, float y_float, float a)
{float coeff[16];cal_cubic_coeff(x_float, y_float, coeff); //计算权重系数float sum = 0.0;int x0 = floor(x_float) - 1;int y0 = floor(y_float) - 1;for (int i = 0; i < 4; i++){for (int j = 0; j < 4; j++){sum += coeff[i * 4 + j] * src.ptr<uchar>(y0 + i)[x0 + j];}}return ((uchar)sum);}
2. SSE指令优化算法
首先,我们来看一下浮点型坐标点周围的4*4个整型点分别在x方向与y方向上与该浮点型坐标点的像素距离,假设浮点型坐标点的x坐标的小数部分为u,y坐标的小数部分为v,那么x方向与y方向上的距离如下图所示(每一格的像素距离为1)。
从左到右,x方向距离分别为1+u、u、1-u、2-u:
从上到下,y方向距离分别为1+v、v、1-v、2-v:
从而得到各个距离的取值范围:
1 ≤ dx0=1+u ≤ 2
0 ≤ dx1=u ≤ 1
0 ≤ dx2=1-u ≤ 1
1 ≤ dx3=2-u ≤ 2
1 ≤ dy0=1+v ≤ 2
0 ≤ dy1=v ≤ 1
0 ≤ dy2=1-v ≤ 1
1 ≤ dy3=2-v ≤ 2
双三次插值算法的权重计算公式为:
我们可以根据取值范围提前确定dxi与dyj的权重函数表达式(之前是分段函数),便于SSE指令的并行计算:
对于dx0、dx3、dy0、dy3,其权重函数表达式为:
对于dx1、dx2、dy1、dy2,其权重函数表达式为:
因此dx0、dx3、dy0、dy3的权重可以并行计算,dx1、dx2、dy1、dy2的权重同样也可以并行计算,假设浮点型坐标为(x, y),权重的SSE指令并行计算代码如下:
float u = x_float - floor(x_float); //计算x坐标额小数部分
float v = y_float - floor(y_float); //计算y坐标额小数部分
float a_mul_4 = (a + a) + (a + a); //提前计算权重公式中的4a
float a_mul_5 = a_mul_4 + a; //提前计算权重公式中的5a
float a_mul_8 = a_mul_4 + a_mul_4; //提前计算权重公式中的8a
float a_add_3 = a + 3; //提前计算权重公式中的a+3
float a_add_2 = a + 2; //提前计算权重公式中的a+2
__m128 a_m = _mm_set1_ps(a); //a a a a
__m128 m_1 = _mm_set1_ps(1.0); //1.0 1.0 1.0 1.0
__m128 a_mul_4_m = _mm_set1_ps(a_mul_4); //4a 4a 4a 4a
__m128 a_mul_5_m = _mm_set1_ps(a_mul_5); //5a 5a 5a 5a
__m128 a_mul_8_m = _mm_set1_ps(a_mul_8); //8a 8a 8a 8a
__m128 a_add_3_m = _mm_set1_ps(a_add_3); //a+3 a+3 a+3 a+3
__m128 a_add_2_m = _mm_set1_ps(a_add_2); //a+2 a+2 a+2 a+2__m128 C30_A30 = _mm_set_ps(2 - v, 1 + v, 2 - u, 1 + u); //dy3 dy0 dx3 dx0
__m128 C21_A21 = _mm_set_ps(1 - v, v, 1 - u, u); //dy2 dy1 dx2 dx1__m128 tmp0 = _mm_sub_ps(_mm_mul_ps(a_m, C30_A30), a_mul_5_m); //a*d - 5a
tmp0 = _mm_add_ps(a_mul_8_m, _mm_mul_ps(C30_A30, tmp0)); //8a + d*(a*d- 5a)
tmp0 = _mm_sub_ps(_mm_mul_ps(C30_A30, tmp0), a_mul_4_m); //d*(8a + d*(a*d- 5a)) - 4a = w(dy3) w(dy0) w(dx3) w(dx0)__m128 tmp1 = _mm_sub_ps(_mm_mul_ps(a_add_2_m, C21_A21), a_add_3_m); //(a+2)*d - (a+3)
tmp1 = _mm_mul_ps(_mm_mul_ps(C21_A21, C21_A21), tmp1); //d*d*((a+2)*d - (a+3))
tmp1 = _mm_add_ps(m_1, tmp1); //1 + d*d*((a+2)*d - (a+3)) = w(dy2) w(dy1) w(dx2) w(dx1)
以上代码运行之后得到权重如下(高位-->低位):
tmp0:w(dy3) w(dy0) w(dx3) w(dx0)
tmp1:w(dy2) w(dy1) w(dx2) w(dx1)
全部的w(dxi)与w(dyj)都已计算完毕,但以上并不是我们想要的排列顺序,我们想要的排列顺序如下:
w(dy3) w(dy2) w(dy1) w(dy0)
w(dx3) w(dx2) w(dx1) w(dx0)
因此我们需要对tmp0与tmp1进行重新打包与排列:
__m128 A_m = _mm_unpacklo_ps(tmp0, tmp1); //交替打包tmp0与tmp1的低位数据:tmp1[1] tmp0[1] tmp1[0] tmp0[0] = w(dx2) w(dx3) w(dx1) w(dx0)
__m128 C_m = _mm_unpackhi_ps(tmp0, tmp1); //交替打包tmp0与tmp1的高位数据:tmp1[3] tmp0[3] tmp1[2] tmp0[2] = w(dy2) w(dy3) w(dy1) w(dy0)
A_m = _mm_shuffle_ps(A_m, A_m, _MM_SHUFFLE(2, 3, 1, 0)); //重新排列A_m中数据的顺序:w(dx3) w(dx2) w(dx1) w(dx0)
C_m = _mm_shuffle_ps(C_m, C_m, _MM_SHUFFLE(2, 3, 1, 0)); //重新排列C_m中数据的顺序:w(dy3) w(dy2) w(dy1) w(dy0)
接下来就可以计算W(i, j)=w(dxi)*w(dyj)了,由于i和j都取0、1、2、3,因此有4*4=16个W(i, j),对应周围的4*4个整型点。代码如下:
__declspec(align(16)) float C[4];_mm_store_ps(C, C_m); //w(dy3) w(dy2) w(dy1) w(dy0)__m128 m128_C = _mm_set1_ps(C[0]); //w(dy0) w(dy0) w(dy0) w(dy0)__m128 coeff0 = _mm_mul_ps(A_m, m128_C); //W(3,0) W(2,0) W(1,0) W(0,0) = w(dx3)*w(dy0) w(dx2)*w(dy0) w(dx1)*w(dy0) w(dx0)*w(dy0)m128_C = _mm_set1_ps(C[1]); //w(dy1) w(dy1) w(dy1) w(dy1)__m128 coeff1 = _mm_mul_ps(A_m, m128_C); //w(dx3)*w(dy1) w(dx2)*w(dy1) w(dx1)*w(dy1) w(dx0)*w(dy1)m128_C = _mm_set1_ps(C[2]); //w(dy2) w(dy2) w(dy2) w(dy2)__m128 coeff2 = _mm_mul_ps(A_m, m128_C); //w(dx3)*w(dy2) w(dx2)*w(dy2) w(dx1)*w(dy2) w(dx0)*w(dy2)m128_C = _mm_set1_ps(C[3]); //w(dy3) w(dy3) w(dy3) w(dy3)__m128 coeff3 = _mm_mul_ps(A_m, m128_C); //w(dx3)*w(dy3) w(dx2)*w(dy3) w(dx1)*w(dy3) w(dx0)*w(dy3)
最后,就可以计算4*4个整型点的像素加权和了:
//计算4*4个整型点组成的矩形点阵的左上角点的坐标,也即(x0, y0)
int x0 = floor(x_float) - 1;
int y0 = floor(y_float) - 1;__m128 sum_m = _mm_setzero_ps(); //0 0 0 0uchar *src_p = src.ptr<uchar>(y0); //4*4矩形点阵的第一行首地址
__m128 src_m = _mm_set_ps(src_p[x0 + 3], src_p[x0 + 2], src_p[x0 + 1], src_p[x0]); //4*4矩形点阵的第一行点像素值:A(x0+3,y0) A(x0+2,y0) A(x0+1,y0) A(x0,y0)
sum_m = _mm_add_ps(sum_m, _mm_mul_ps(src_m, coeff0)); //累加:W(3,0)*A(x0+3,y0) W(2,0)*A(x0+2,y0) W(1,0)*A(x0+1,y0) W(0,0)*A(x0,y0) src_p = src.ptr<uchar>(y0 + 1); //4*4矩形点阵的第二行首地址
src_m = _mm_set_ps(src_p[x0 + 3], src_p[x0 + 2], src_p[x0 + 1], src_p[x0]); //4*4矩形点阵的第二行点像素值:A(x0+3,y1) A(x0+2,y1) A(x0+1,y1) A(x0,y1)
sum_m = _mm_add_ps(sum_m, _mm_mul_ps(src_m, coeff1)); //累加:W(3,1)*A(x0+3,y1) W(2,1)*A(x0+2,y1) W(1,1)*A(x0+1,y1) W(0,1)*A(x0,y1)src_p = src.ptr<uchar>(y0 + 2); //4*4矩形点阵的第三行首地址
src_m = _mm_set_ps(src_p[x0 + 3], src_p[x0 + 2], src_p[x0 + 1], src_p[x0]); //4*4矩形点阵的第三行点像素值:A(x0+3,y2) A(x0+2,y2) A(x0+1,y2) A(x0,y2)
sum_m = _mm_add_ps(sum_m, _mm_mul_ps(src_m, coeff2)); //累加:W(3,2)*A(x0+3,y2) W(2,2)*A(x0+2,y2) W(1,2)*A(x0+1,y2) W(0,2)*A(x0,y2)src_p = src.ptr<uchar>(y0 + 3); //4*4矩形点阵的第四行首地址
src_m = _mm_set_ps(src_p[x0 + 3], src_p[x0 + 2], src_p[x0 + 1], src_p[x0]); //4*4矩形点阵的第四行点像素值:A(x0+3,y3) A(x0+2,y3) A(x0+1,y3) A(x0,y3)
sum_m = _mm_add_ps(sum_m, _mm_mul_ps(src_m, coeff3)); //累加:W(3,3)*A(x0+3,y3) W(2,3)*A(x0+2,y3) W(1,3)*A(x0+1,y3) W(0,3)*A(x0,y3)float *p = (float *)&sum_m;
uchar sum = (uchar)(p[0] + p[1] + p[2] + p[3]); //最后再把sum_m中的四个累加和加起来,即得到最终的插值结果
完整的SSE指令优化的双三次插值代码如下:
uchar cubic_inner_SSE(Mat src, float x_float, float y_float, float a)
{//计算权重系数float u = x_float - floor(x_float);float v = y_float - floor(y_float);float a_mul_4 = (a + a) + (a + a); //4afloat a_mul_5 = a_mul_4 + a; //5afloat a_mul_8 = a_mul_4 + a_mul_4; //8afloat a_add_3 = a + 3;float a_add_2 = a + 2;__m128 a_m = _mm_set1_ps(a);__m128 m_1 = _mm_set1_ps(1.0);__m128 a_mul_4_m = _mm_set1_ps(a_mul_4);__m128 a_mul_5_m = _mm_set1_ps(a_mul_5);__m128 a_mul_8_m = _mm_set1_ps(a_mul_8);__m128 a_add_3_m = _mm_set1_ps(a_add_3);__m128 a_add_2_m = _mm_set1_ps(a_add_2);__m128 C30_A30 = _mm_set_ps(2 - v, 1 + v, 2 - u, 1 + u); //C3 C0 A3 A0__m128 C21_A21 = _mm_set_ps(1 - v, v, 1 - u, u); //C2 C1 A2 A1__m128 tmp0 = _mm_sub_ps(_mm_mul_ps(a_m, C30_A30), a_mul_5_m); //a*xx - a_mul_5tmp0 = _mm_add_ps(a_mul_8_m, _mm_mul_ps(C30_A30, tmp0)); //a_mul_8 + xx*(a*xx - a_mul_5)tmp0 = _mm_sub_ps(_mm_mul_ps(C30_A30, tmp0), a_mul_4_m); //xx*(a_mul_8 + xx*(a*xx - a_mul_5)) - a_mul_4 = C3 C0 A3 A0__m128 tmp1 = _mm_sub_ps(_mm_mul_ps(a_add_2_m, C21_A21), a_add_3_m); //a_add_2*xx - a_add_3tmp1 = _mm_mul_ps(_mm_mul_ps(C21_A21, C21_A21), tmp1); //xx*xx*(a_add_2*xx - a_add_3)tmp1 = _mm_add_ps(m_1, tmp1); //1 + xx*xx*(a_add_2*xx - a_add_3) = C2 C1 A2 A1__m128 A_m = _mm_unpacklo_ps(tmp0, tmp1); //tmp1[1] tmp0[1] tmp1[0] tmp0[0] = A2 A3 A1 A0__m128 C_m = _mm_unpackhi_ps(tmp0, tmp1); //tmp1[3] tmp0[3] tmp1[2] tmp0[2] = C2 C3 C1 C0A_m = _mm_shuffle_ps(A_m, A_m, _MM_SHUFFLE(2, 3, 1, 0)); //A3 A2 A1 A0C_m = _mm_shuffle_ps(C_m, C_m, _MM_SHUFFLE(2, 3, 1, 0)); //C3 C2 C1 C0__declspec(align(16)) float C[4];_mm_store_ps(C, C_m);__m128 m128_C = _mm_set1_ps(C[0]);__m128 coeff0 = _mm_mul_ps(A_m, m128_C);m128_C = _mm_set1_ps(C[1]);__m128 coeff1 = _mm_mul_ps(A_m, m128_C);m128_C = _mm_set1_ps(C[2]);__m128 coeff2 = _mm_mul_ps(A_m, m128_C);m128_C = _mm_set1_ps(C[3]);__m128 coeff3 = _mm_mul_ps(A_m, m128_C);///int x0 = floor(x_float) - 1;int y0 = floor(y_float) - 1;__m128 sum_m = _mm_setzero_ps();uchar *src_p = src.ptr<uchar>(y0);__m128 src_m = _mm_set_ps(src_p[x0 + 3], src_p[x0 + 2], src_p[x0 + 1], src_p[x0]);sum_m = _mm_add_ps(sum_m, _mm_mul_ps(src_m, coeff0));src_p = src.ptr<uchar>(y0 + 1);src_m = _mm_set_ps(src_p[x0 + 3], src_p[x0 + 2], src_p[x0 + 1], src_p[x0]);sum_m = _mm_add_ps(sum_m, _mm_mul_ps(src_m, coeff1));src_p = src.ptr<uchar>(y0 + 2);src_m = _mm_set_ps(src_p[x0 + 3], src_p[x0 + 2], src_p[x0 + 1], src_p[x0]);sum_m = _mm_add_ps(sum_m, _mm_mul_ps(src_m, coeff2));src_p = src.ptr<uchar>(y0 + 3);src_m = _mm_set_ps(src_p[x0 + 3], src_p[x0 + 2], src_p[x0 + 1], src_p[x0]);sum_m = _mm_add_ps(sum_m, _mm_mul_ps(src_m, coeff3));float *p = (float *)&sum_m;uchar sum = (uchar)(p[0] + p[1] + p[2] + p[3]);return sum;
}
接下来,我们分别调用以上实现的cubic_inner函数和cubic_inner_SSE函数来实现图像缩放功能,实现代码如下:
//图像缩放函数
void resize_img(Mat src, Mat &dst, float row_m, float col_m)
{const int row = (int)(src.rows*row_m);const int col = (int)(src.cols*col_m);const float x_a = 1.0 / col_m;const float y_a = 1.0 / row_m;Mat dst_tmp = Mat::zeros(row, col, CV_8UC1);for (int i = 0; i < row; i++){uchar *p = dst_tmp.ptr<uchar>(i);float y = i*y_a;for (int j = 0; j < col; j++){float x = j*x_a;//p[j] = cubic_inner(src, x, y, -0.5); //原函数p[j] = cubic_inner_SSE(src, x, y, -0.5); //SSE优化函数}}dst_tmp.copyTo(dst);
}
自己实现了一个微秒级计时的类,用于记录函数的运行时间:
class Timer_Us
{private:LARGE_INTEGER cpuFreq;LARGE_INTEGER startTime;LARGE_INTEGER endTime;public:double rumTime;void get_frequence(void);void start_timer(void);void stop_timer(char *str);Timer_Us(); //构造函数~Timer_Us(); //析构函数
};void Timer_Us::get_frequence(void)
{QueryPerformanceFrequency(&cpuFreq); //获取时钟频率
}void Timer_Us::start_timer(void)
{QueryPerformanceCounter(&startTime); //开始计时
}void Timer_Us::stop_timer(char *str)
{QueryPerformanceCounter(&endTime); //结束计时rumTime = (((endTime.QuadPart - startTime.QuadPart) * 1000.0f) / cpuFreq.QuadPart);cout <<str<< rumTime << " ms" << endl;
}Timer_Us::Timer_Us() //构造函数
{QueryPerformanceFrequency(&cpuFreq);
}Timer_Us::~Timer_Us() //析构函数
{}
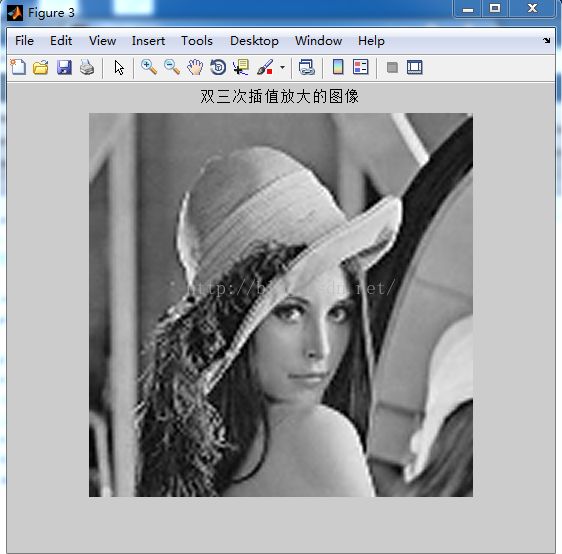
最后是测试函数,调用以上实现的图像缩放函数,对248*236的Lena图像的宽和高都放大到原来的三倍,并记录SSE指令优化插值前后的耗时。
void resize_img_test(void)
{Mat img = imread("lena.tif", CV_LOAD_IMAGE_GRAYSCALE);Timer_Us timer;float mul = 3; //宽和高都放大三倍Mat img_resize;timer.start_timer(); //开始计时resize_img(img, img_resize2, mul, mul, 2);timer.stop_timer("cubic resize time:"); //结束计时,并显示运行耗时imshow("cubic img_resize", img_resize);waitKey();
}
运行以上代码,调用原C++实现的cubic_inner函数,耗时约35.5022 ms,如果是调用SSE指令优化的cubic_inner_SSE函数,耗时约17.3297 ms。因此SSE优化之后,耗时减少约一半,优化效果还是比较理想的。
原图
放大的图像
实际上以上实现的图像缩放函数resize_img还有很大的优化空间,比如函数里面有两层循环,外面一层是行遍历,里面一层是列遍历,在双三次插值过程中,有一些参数的计算对于同一行数据来说是一样的,因此可以把这部分计算过程从内循环提到外循环来做,如此以来,每一行只需要计算一次这些参数,可以减少不少耗时。进一步优化的resize_img函数代码如下。调用该函数对同样的Lena图像进行宽、高各三倍的放大,耗时减少为10 ms左右,优化效果还是比较显著的。
void resize_img_cubic(Mat src, Mat &dst, float row_m, float col_m)
{const int row = (int)(src.rows*row_m);const int col = (int)(src.cols*col_m);const float x_a = 1.0 / col_m;const float y_a = 1.0 / row_m;Mat dst_tmp = Mat::zeros(row, col, CV_8UC1);__declspec(align(16)) float A[4]; //内存对齐float C[4];float a = -0.15;//这些参数不变,直接提到循环外面计算float a_mul_4 = (a + a) + (a + a); //4afloat a_mul_5 = a_mul_4 + a; //5afloat a_mul_8 = a_mul_4 + a_mul_4; //8afloat a_add_3 = a + 3;float a_add_2 = a + 2;float xx;for (int i = 0; i < row; i++){uchar *p = dst_tmp.ptr<uchar>(i);//以下这些是提到外循环计算的参数float y = i*y_a;int y0 = floor(y) - 1;float v = y - floor(y);xx = 1 + v;C[0] = -a_mul_4 + xx*(a_mul_8 + xx*(a*xx - a_mul_5)); //1<u<2xx = v; // 0<v<1;C[1] = 1 + xx*xx*(a_add_2*xx - a_add_3);xx = 1 - v; // 0<v<1C[2] = 1 + xx*xx*(a_add_2*xx - a_add_3);xx = 2 - v; // 1<v<2C[3] = -a_mul_4 + xx*(a_mul_8 + xx*(a*xx - a_mul_5));__m128 m128_C0 = _mm_set1_ps(C[0]);__m128 m128_C1 = _mm_set1_ps(C[1]);__m128 m128_C2 = _mm_set1_ps(C[2]);__m128 m128_C3 = _mm_set1_ps(C[3]);uchar *src_p0 = src.ptr<uchar>(y0);uchar *src_p1 = src.ptr<uchar>(y0+1);uchar *src_p2 = src.ptr<uchar>(y0+2);uchar *src_p3 = src.ptr<uchar>(y0+3);for (int j = 0; j < col; j++){float x = j*x_a;float u = x - floor(x);xx = 1 + u;A[0] = -a_mul_4 + xx*(a_mul_8 + xx*(a*xx - a_mul_5)); //-a_mul_4 + a_mul_8*u - a_mul_5*u*u + a*u*u*u; //1<u<2xx = u; // 0<u<1;A[1] = 1 + xx*xx*(a_add_2*xx - a_add_3); //1 - a_add_3*xx*xx + a_add_2*xx*xx*xx;xx = 1 - u; // 0<u<1A[2] = 1 + xx*xx*(a_add_2*xx - a_add_3);//1 - a_add_3*xx*xx + a_add_2*xx*xx*xx;xx = 2 - u; // 1<u<2A[3] = -a_mul_4 + xx*(a_mul_8 + xx*(a*xx - a_mul_5));//-a_mul_4 + a_mul_8*xx - a_mul_5*xx*xx + a*xx*xx*xx;__m128 m128_A = _mm_load_ps(A);__m128 coeff0 = _mm_mul_ps(m128_A, m128_C0);__m128 coeff1 = _mm_mul_ps(m128_A, m128_C1);__m128 coeff2 = _mm_mul_ps(m128_A, m128_C2);__m128 coeff3 = _mm_mul_ps(m128_A, m128_C3);int x0 = floor(x) - 1;__m128 src_m = _mm_set_ps(src_p0[x0 + 3], src_p0[x0 + 2], src_p0[x0 + 1], src_p0[x0]);__m128 sum_m = _mm_mul_ps(src_m, coeff0);src_m = _mm_set_ps(src_p1[x0 + 3], src_p1[x0 + 2], src_p1[x0 + 1], src_p1[x0]);sum_m = _mm_add_ps(sum_m, _mm_mul_ps(src_m, coeff1));src_m = _mm_set_ps(src_p2[x0 + 3], src_p2[x0 + 2], src_p2[x0 + 1], src_p2[x0]);sum_m = _mm_add_ps(sum_m, _mm_mul_ps(src_m, coeff2));src_m = _mm_set_ps(src_p3[x0 + 3], src_p3[x0 + 2], src_p3[x0 + 1], src_p3[x0]);sum_m = _mm_add_ps(sum_m, _mm_mul_ps(src_m, coeff3));float *p1 = (float *)&sum_m;p[j] = (uchar)(p1[0] + p1[1] + p1[2] + p1[3]);}}dst_tmp.copyTo(dst);}
学习代码优化有一段时间了,包括代码自身结构优化、SSE指令优化、CUDA优化等。感触最深的是,代码优化是一个精益求精的过程,一步步地优化之后,往往优化代码与原来的代码相比已经面目全非了,因此优化之后的代码可读性非常差,如果不对自己的优化思路作详细记录,过一段时间可能自己都看不懂自己的优化代码了,这是非常尴尬的,所以详细记录与注释还是非常有必要的。当然,本人的水平有限,以上代码的优化只是一个抛砖引玉的过程,也许还有更大的优化空间,如果读者有更好的优化idea,欢迎给我留言讨论。
微信公众号如下,欢迎扫码关注,欢迎私信技术交流: