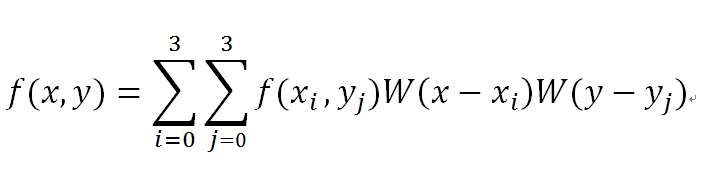双三次插值 - 插值图像任意位置亚像素C++

article/2025/9/23 16:15:02

双三次插值 - 插值图像任意位置亚像素C++

一、概念

双三次插值又称立方卷积插值。三次卷积插值是一种更加复杂的插值方式。该算法利用待采样点周围16个点的灰度值作三次插值，不仅考虑到4 个直接相邻点的灰度影响，而且考虑到各邻点间灰度值变化率的影响。三次运算可得到更接近高分辨率图像的放大效果，但也导致了运算量的急剧增加。这种算法需要选取插值基函数来拟合数据，其最常用的插值基函数如图1所示，本次实验采用如图所示函数作为基函数。

图1

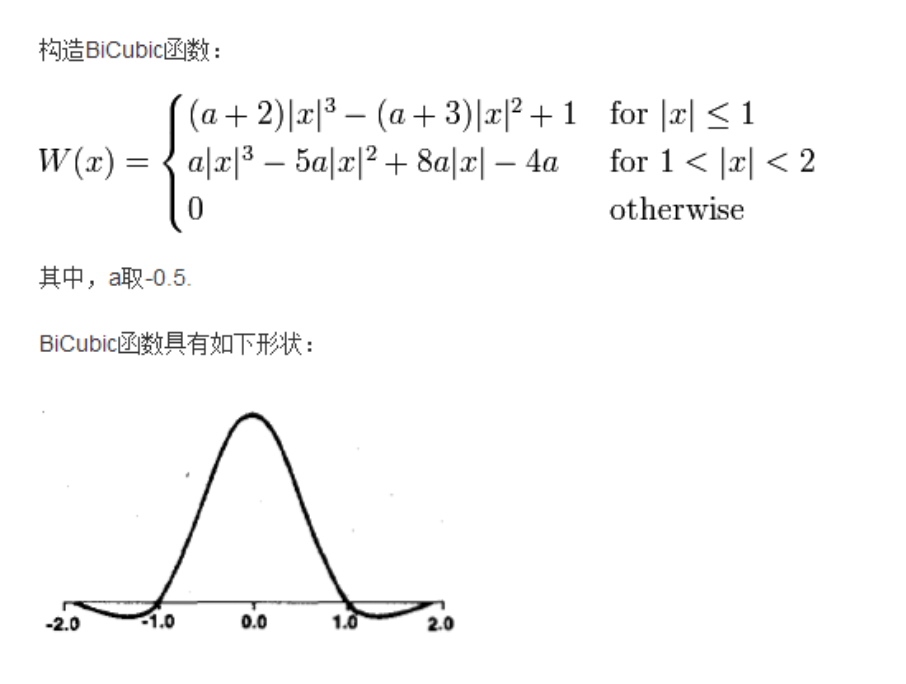
加权算法（a可以不取-0.5）：点开链接

根据比例关系x/X=m/M=1/K，我们可以得到B(X,Y)在A上的对应坐标为A(x,y)=A(X*(m/M),Y*(n/N))=A(X/K,Y/K)。如图所示P点就是目标图像B在(X,Y)处对应于源图像A中的位置，P的坐标位置会出现小数部分，所以我们假设 P的坐标为P(x+u,y+v)，其中x,y分别表示整数部分，u,v分别表示小数部分（蓝点到a11方格中红点的距离）。那么我们就可以得到如图所示的最近16个像素的位置，在这里用a(i,j)(i,j=0,1,2,3)来表示，如下图。

图

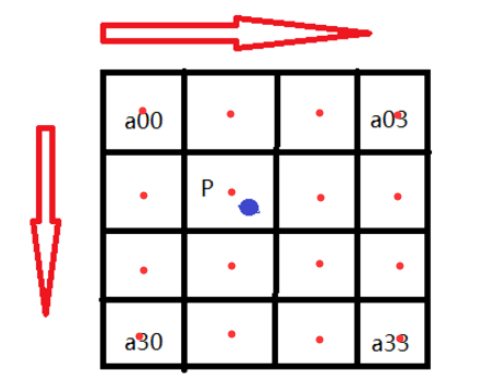
我们要做的就是求出BiCubic函数中的参数x,从而获得上面所说的16个像素所对应的权重W(x)。BiCubic基函数是一维的，而像素是二维的，所以我们将像素点的行与列分开计算。BiCubic函数中的参数x表示该像素点到P点的距离，例如a00距离P(x+u,y+v)的距离为(1+u,1+v)，因此a00的横坐标权重i_0=W(1+u)，纵坐标权重j_0=W(1+v)，a00对B(X,Y)的贡献值为：（a00像素值）* i_0* j_0。因此，a0X的横坐标权重分别为W(1+u)，W(u)，W(1-u)，W(2-u)；ay0的纵坐标权重分别为W(1+v)，W(v)，W(1-v)，W(2-v)；B(X,Y)像素值为：

图

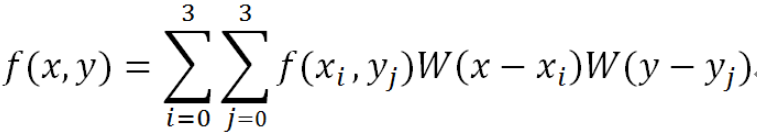
二、代码实现C++(可配合读取图片程序使用)

#include <iostream>
#include <tchar.h>
#include "ImageBuffer.h"using namespace CamCtrl;void test()
{CImageBuffer mCImageBuffer;mCImageBuffer.LoadFromBmp(_T("1.bmp"));
}int main()
{test();return 0;
}

//功能：双三边插值
//image：输入图片
//iImgWidth：图像宽度
//iImgHeight：图像高度
//dx，dy：亚像素点与整像素点posy在下x，y上的距离
//ipos = (posy - 1)*(iImgWidth)+(posx - 1);  //得到ipos
double CubicPolynomial(unsigned char * image, int iImgWidth, int iImgHeight, double dx, double dy, int ipos)
{// image为图像各个位置的像素值， iImgWidth为图像的宽度, iImgHeight为图像的高度, ipos为当前插值的位置。// 先计算padding 图像的大小。int padding_size = (iImgHeight + 2) * (iImgWidth + 2);double * padding_img = new double[padding_size];// 接着对 padding_img 进行赋值。// 将原图像的值赋给padding_img的(2,2)-(iImgHeight+1, iImgWidth+1)// 该部分验证无误。for (int i = 0; i < iImgHeight; i++){for (int j = 0; j < iImgWidth; j++){int ipos1 = (i + 1) * (iImgWidth + 2) + (j + 1);int temp = i * iImgWidth + j;padding_img[ipos1] = image[temp];}}// 第一行的值： 第二行、第三行、第四行的值的线性组合.// 该部分验证无误。for (int i = 1; i < iImgWidth + 1; i++){int ipos1 = i;double temp1 = padding_img[ipos1 + iImgWidth + 2];double temp2 = padding_img[ipos1 + 2 * (iImgWidth + 2)];double temp3 = padding_img[ipos1 + 3 * (iImgWidth + 2)];padding_img[ipos1] = 3 * temp1 - 3 * temp2 + temp3;}// 最后一行的值：倒数第二、第三、第四行的值的线性组合。// 该部分验证无误。for (int i = 1; i < iImgWidth + 1; i++){int ipos1 = i + (iImgHeight + 1)*(iImgWidth + 2);double temp1 = padding_img[ipos1 - (iImgWidth + 2)];double temp2 = padding_img[ipos1 - 2 * (iImgWidth + 2)];double temp3 = padding_img[ipos1 - 3 * (iImgWidth + 2)];padding_img[ipos1] = 3 * temp1 - 3 * temp2 + temp3;}// 第一列的值：第二列、第三列、第四列的值的线性组合。// 该部分验证无误。for (int i = 1; i < iImgHeight + 1; i++){int ipos1 = i * (iImgWidth + 2);double temp1 = padding_img[ipos1 + 1];double temp2 = padding_img[ipos1 + 2];double temp3 = padding_img[ipos1 + 3];padding_img[ipos1] = 3 * temp1 - 3 * temp2 + temp3;}// 最后一列的值：倒数第二、第三、第四列的值的线性组合。// 该部分验证无误。for (int i = 1; i < iImgHeight + 1; i++){int ipos1 = (i + 1)*(iImgWidth + 2) - 1;double temp1 = padding_img[ipos1 - 1];double temp2 = padding_img[ipos1 - 2];double temp3 = padding_img[ipos1 - 3];padding_img[ipos1] = 3 * temp1 - 3 * temp2 + temp3;}// 后面4个点的组合方向均为列的方向。即ipos+1, ipos+2, ipos+3，或ipos-1, ipos-2, ipos-3.// 左上角的点。padding_img[0] = 3 * padding_img[1] - 3 * padding_img[2] + padding_img[3];// 右上角的点。padding_img[iImgWidth + 1] = 3 * padding_img[iImgWidth] - 3 * padding_img[iImgWidth - 1] + padding_img[iImgWidth - 2];// 左下角的点。int pos_left_bottom = (iImgHeight + 1)*(iImgWidth + 2);padding_img[pos_left_bottom] = 3 * padding_img[pos_left_bottom + 1] - 3 * padding_img[pos_left_bottom + 2] + padding_img[pos_left_bottom + 3];// 右下角的点。int pos_right_bottom = (iImgHeight + 2)*(iImgWidth + 2) - 1;padding_img[pos_right_bottom] = 3 * padding_img[pos_right_bottom - 1] - 3 * padding_img[pos_right_bottom - 2] + padding_img[pos_right_bottom - 3];// padding结束之后，进行插值操作。首先要把原图的ipos对应到新图的ipos。int height = (ipos + 1) / iImgWidth;int width = (ipos + 1) - height * iImgWidth;// 在新图中的位置。int new_ipos = width + (height + 1) * (iImgWidth + 2);// x方向卷积double dx_2 = dx * dx;double dx_3 = dx * dx*dx;double a4 = (-dx_3 + 2 * dx_2 - dx) / 2;double a5 = (3 * dx_3 - 5 * dx_2 + 2) / 2;double a6 = (-3 * dx_3 + 4 * dx_2 + dx) / 2;double a7 = (dx_3 - dx_2) / 2;double a8 = a4 * padding_img[new_ipos - 1 - (iImgWidth + 2)] + a5 * padding_img[new_ipos - (iImgWidth + 2)] + a6 * padding_img[new_ipos + 1 - (iImgWidth + 2)] + a7 * padding_img[new_ipos + 2 - (iImgWidth + 2)];double a9 = a4 * padding_img[new_ipos - 1] + a5 * padding_img[new_ipos] + a6 * padding_img[new_ipos + 1] + a7 * padding_img[new_ipos + 2];double a10 = a4 * padding_img[new_ipos - 1 + (iImgWidth + 2)] + a5 * padding_img[new_ipos + (iImgWidth + 2)] + a6 * padding_img[new_ipos + 1 + (iImgWidth + 2)] + a7 * padding_img[new_ipos + 2 + (iImgWidth + 2)];double a11 = a4 * padding_img[new_ipos - 1 + 2 * (iImgWidth + 2)] + a5 * padding_img[new_ipos + 2 * (iImgWidth + 2)] + a6 * padding_img[new_ipos + 1 + 2 * (iImgWidth + 2)] + a7 * padding_img[new_ipos + 2 + 2 * (iImgWidth + 2)];// y方向卷积double dy_2 = dy * dy;double dy_3 = dy * dy*dy;double a12 = (-dy_3 + 2 * dy_2 - dy) / 2;double a13 = (3 * dy_3 - 5 * dy_2 + 2) / 2;double a14 = (-3 * dy_3 + 4 * dy_2 + dy) / 2;double a15 = (dy_3 - dy_2) / 2;double gray_value;gray_value = a8 * a12 + a9 * a13 + a10 * a14 + a11 * a15;delete padding_img;return gray_value;}

三、C++代码（基于opencv）

#include <vector>
#include "opencv2/core.hpp"
#include "opencv2/imgproc.hpp"
#include "opencv2/imgcodecs.hpp"
#include <opencv2/opencv.hpp>
#include "bmptools.h"
#include <cstdlib>
using namespace std;using namespace cv;double CubicPolynomial(cv::Mat pGray, double dx, double dy, int posx, int posy)
{	int rows = pGray.rows;int cols = pGray.cols;// 创建padding一圈的图像，用来做卷积cv::Mat padded_image = cv::Mat::zeros(rows + 2, cols + 2, CV_64FC1);// 将原始图像放置padding图像的中间for (int i = 1; i < padded_image.rows-1; i++){	for (int j = 1; j < padded_image.cols-1; j++){double temp = pGray.at<uchar>(i - 1, j - 1);padded_image.at<double>(i, j) = temp;}}// 分别计算周围padding一圈的像素值for (int j = 1; j < padded_image.cols-1; j++){// 第一行padded_image.at<double>(0, j) = 3 * padded_image.at<double>(1, j) - 3 * padded_image.at<double>(2, j) + padded_image.at<double>(3, j);//最后一行padded_image.at<double>(rows + 1, j) = 3 * padded_image.at<double>(rows, j) - 3 * padded_image.at<double>(rows - 1, j) + padded_image.at<double>(rows - 2, j);}for (int i = 1; i < padded_image.rows-1; i++){// 第一列padded_image.at<double>(i, 0) = 3 * padded_image.at<double>(i, 1) - 3 * padded_image.at<double>(i, 2) + padded_image.at<double>(i, 3);// 最后一列padded_image.at<double>(i, cols + 1) = 3 * padded_image.at<double>(i, cols) - 3 * padded_image.at<double>(i, cols - 1) + padded_image.at<double>(i, cols - 2);}padded_image.at<double>(0, 0) = 3 * padded_image.at<double>(0, 1) - 3 * padded_image.at<double>(0, 2) + padded_image.at<double>(0, 3);padded_image.at<double>(0, cols + 1) = 3 * padded_image.at<double>(0, cols) - 3 * padded_image.at<double>(0, cols - 1) + padded_image.at<double>(0, cols - 2);padded_image.at<double>(rows + 1, 0) = 3 * padded_image.at<double>(rows + 1, 1) - 3 * padded_image.at<double>(rows + 1, 2) + padded_image.at<double>(rows + 1, 3);padded_image.at<double>(rows + 1, cols + 1) = 3 * padded_image.at<double>(rows + 1, cols) - 3 * padded_image.at<double>(rows + 1, cols - 1) + padded_image.at<double>(rows + 1, cols - 2);// 卷积的过程// x方向卷积double dx_2 = dx*dx;double dx_3 = dx*dx*dx;double a4 = (-dx_3 + 2 * dx_2 - dx) / 2;double a5 = (3 * dx_3 - 5 * dx_2 + 2) / 2;double a6 = (-3 * dx_3 + 4 * dx_2 + dx) / 2;double a7 = (dx_3 - dx_2) / 2;double a8 = a4*padded_image.at<double>(posy - 1, posx - 1) + a5*padded_image.at<double>(posy - 1, posx) + a6*padded_image.at<double>(posy - 1, posx + 1) + a7*padded_image.at<double>(posy - 1, posx + 2);double a9 = a4*padded_image.at<double>(posy, posx - 1) + a5*padded_image.at<double>(posy, posx) + a6*padded_image.at<double>(posy, posx + 1) + a7*padded_image.at<double>(posy, posx + 2);double a10 = a4*padded_image.at<double>(posy + 1, posx - 1) + a5*padded_image.at<double>(posy + 1, posx) + a6*padded_image.at<double>(posy + 1, posx + 1) + a7*padded_image.at<double>(posy + 1, posx + 2);double a11 = a4*padded_image.at<double>(posy + 2, posx - 1) + a5*padded_image.at<double>(posy + 2, posx) + a6*padded_image.at<double>(posy + 2, posx + 1) + a7*padded_image.at<double>(posy + 2, posx + 2);// y方向卷积double dy_2 = dy*dy;double dy_3 = dy*dy*dy;double a12 = (-dy_3 + 2 * dy_2 - dy) / 2;double a13 = (3 * dy_3 - 5 * dy_2 + 2) / 2;double a14 = (-3 * dy_3 + 4 * dy_2 + dy) / 2;double a15 = (dy_3 - dy_2) / 2;double gray_value;gray_value = a8*a12 + a9*a13 + a10*a14 + a11*a15;return gray_value;
}// 这里的ipos是原图像中的位置，要把它对应到padding后图像的ipos，才能进行插值计算。double CubicPolynomial(unsigned char * image, int iImgWidth, int iImgHeight, double dx, double dy, int ipos)
{// image为图像各个位置的像素值， iImgWidth为图像的宽度, iImgHeight为图像的高度, ipos为当前插值的位置。// 先计算padding 图像的大小。int padding_size = (iImgHeight + 2) * (iImgWidth + 2);double * padding_img = new double[padding_size];// 接着对 padding_img 进行赋值。// 将原图像的值赋给padding_img的(2,2)-(iImgHeight+1, iImgWidth+1)// 该部分验证无误。for (int i = 0; i < iImgHeight; i++){for (int j = 0; j < iImgWidth; j++){int ipos1 = (i+1) * (iImgWidth+2) + (j+1);int temp = i*iImgWidth + j;padding_img[ipos1] = image[temp];}}// 第一行的值： 第二行、第三行、第四行的值的线性组合.// 该部分验证无误。for (int i = 1; i < iImgWidth+1; i++){int ipos1 = i;double temp1 = padding_img[ipos1 + iImgWidth + 2];double temp2 = padding_img[ipos1 + 2 * (iImgWidth + 2)];double temp3 = padding_img[ipos1 + 3 * (iImgWidth + 2)];padding_img[ipos1] = 3 * temp1 - 3 * temp2 + temp3;}// 最后一行的值：倒数第二、第三、第四行的值的线性组合。// 该部分验证无误。for (int i = 1; i < iImgWidth+1; i++){int ipos1 = i + (iImgHeight + 1)*(iImgWidth + 2);double temp1 = padding_img[ipos1 - (iImgWidth + 2)];double temp2 = padding_img[ipos1 - 2 * (iImgWidth + 2)];double temp3 = padding_img[ipos1 - 3 * (iImgWidth + 2)];padding_img[ipos1] = 3 * temp1 - 3 * temp2 + temp3;}// 第一列的值：第二列、第三列、第四列的值的线性组合。// 该部分验证无误。for (int i = 1; i < iImgHeight+1; i++){int ipos1 = i * (iImgWidth + 2);double temp1 = padding_img[ipos1 + 1];double temp2 = padding_img[ipos1 + 2];double temp3 = padding_img[ipos1 + 3];padding_img[ipos1] = 3 * temp1 - 3 * temp2 + temp3;}// 最后一列的值：倒数第二、第三、第四列的值的线性组合。// 该部分验证无误。for (int i = 1; i < iImgHeight+1; i++){int ipos1 = (i + 1)*(iImgWidth + 2) - 1;double temp1 = padding_img[ipos1 - 1];double temp2 = padding_img[ipos1 - 2];double temp3 = padding_img[ipos1 - 3];padding_img[ipos1] = 3 * temp1 - 3 * temp2 + temp3;}// 后面4个点的组合方向均为列的方向。即ipos+1, ipos+2, ipos+3，或ipos-1, ipos-2, ipos-3.// 左上角的点。padding_img[0] = 3 * padding_img[1] - 3 * padding_img[2] + padding_img[3];// 右上角的点。padding_img[iImgWidth + 1] = 3 * padding_img[iImgWidth] - 3 * padding_img[iImgWidth - 1] + padding_img[iImgWidth - 2];// 左下角的点。int pos_left_bottom = (iImgHeight + 1)*(iImgWidth + 2);padding_img[pos_left_bottom] = 3 * padding_img[pos_left_bottom + 1] - 3 * padding_img[pos_left_bottom + 2] + padding_img[pos_left_bottom + 3];// 右下角的点。int pos_right_bottom = (iImgHeight + 2)*(iImgWidth + 2) - 1;padding_img[pos_right_bottom] = 3 * padding_img[pos_right_bottom - 1] - 3 * padding_img[pos_right_bottom - 2] + padding_img[pos_right_bottom - 3];// padding结束之后，进行插值操作。首先要把原图的ipos对应到新图的ipos。int height = (ipos + 1) / iImgWidth;int width = (ipos + 1) - height*iImgWidth;// 在新图中的位置。int new_ipos = width + (height+1) * (iImgWidth + 2);// x方向卷积double dx_2 = dx*dx;double dx_3 = dx*dx*dx;double a4 = (-dx_3 + 2 * dx_2 - dx) / 2;double a5 = (3 * dx_3 - 5 * dx_2 + 2) / 2;double a6 = (-3 * dx_3 + 4 * dx_2 + dx) / 2;double a7 = (dx_3 - dx_2) / 2;double a8 = a4*padding_img[new_ipos - 1 - (iImgWidth + 2)] + a5*padding_img[new_ipos - (iImgWidth + 2)] + a6 * padding_img[new_ipos + 1 - (iImgWidth + 2)] + a7 * padding_img[new_ipos + 2 - (iImgWidth + 2)];double a9 = a4*padding_img[new_ipos - 1] + a5*padding_img[new_ipos] + a6 * padding_img[new_ipos + 1] + a7 * padding_img[new_ipos + 2];double a10 = a4*padding_img[new_ipos - 1 + (iImgWidth + 2)] + a5*padding_img[new_ipos + (iImgWidth + 2)] + a6 * padding_img[new_ipos + 1 + (iImgWidth + 2)] + a7 * padding_img[new_ipos + 2 + (iImgWidth + 2)];double a11 = a4*padding_img[new_ipos - 1 + 2 * (iImgWidth + 2)] + a5*padding_img[new_ipos + 2 * (iImgWidth + 2)] + a6 * padding_img[new_ipos + 1 + 2 * (iImgWidth + 2)] + a7 * padding_img[new_ipos + 2 + 2 * (iImgWidth + 2)];// y方向卷积double dy_2 = dy*dy;double dy_3 = dy*dy*dy;double a12 = (-dy_3 + 2 * dy_2 - dy) / 2;double a13 = (3 * dy_3 - 5 * dy_2 + 2) / 2;double a14 = (-3 * dy_3 + 4 * dy_2 + dy) / 2;double a15 = (dy_3 - dy_2) / 2;double gray_value;gray_value = a8*a12 + a9*a13 + a10*a14 + a11*a15;return gray_value;}int main(int argc, char **argv)
{// imageData为图像数据，unsigned char * 型Mat image = imread("F:\\img\\image\\result1.jpg", 0);int image_size = image.cols * image.rows;unsigned char* imageData = new unsigned char[image_size];int a = 0;for (int i = 0; i<image.rows; i++){for (int j = 0; j<image.cols; j++){imageData[a] = image.at<uchar>(i, j);a++;}}int iImgHeight = image.rows;int iImgWidth = image.cols;// 进行多次随机试验。for (int i = 0; i < 1000; i++){// x是列方向，y是行方向，在cv::Mat做输入的函数中，起始点为(1,1)点。// 生成随机位置。int x = rand() % (iImgWidth - 1) + 1;int y = rand() % (iImgHeight - 1) + 1;// 对应回原图像下的ipos。int ipos = (y - 1)*(iImgWidth)+(x - 1);// 生成随机的dx, dy.int N = 10000;double dx = rand() % (N + 1) / (float)(N + 1);;double dy = rand() % (N + 1) / (float)(N + 1);;// 基于unsigned char * 数据的插值结果。double temp1 = CubicPolynomial(imageData, iImgWidth, iImgHeight, dx, dy, ipos);// 基于cv::Mat 数据的插值结果。double temp2 = CubicPolynomial(image, dx, dy, x, y);double difference = abs(temp2 - temp1);cout << "The difference is : " << difference << endl;}system("pause");return 0;
}

四、Matlab代码

function Value = CubicInterpoly(y,x,img)uw = floor(x);vw = floor(y);pV = zeros(16,1);W = zeros(16,2);pV(1) = img(vw-1,uw-1);W(1,:) = BiCubic(y,x,vw-1,uw-1);pV(2) = img(vw-1,uw);W(2,:) = BiCubic(y,x,vw-1,uw);pV(3) = img(vw-1,uw+1);W(3,:) = BiCubic(y,x,vw-1,uw+1);pV(4) = img(vw-1,uw+2);W(4,:) = BiCubic(y,x,vw-1,uw+2);pV(5) = img(vw,uw-1);W(5,:) = BiCubic(y,x,vw,uw-1);pV(6) = img(vw,uw);W(6,:) = BiCubic(y,x,vw,uw);pV(7) = img(vw,uw+1);W(7,:) = BiCubic(y,x,vw,uw+1);pV(8) = img(vw,uw+2);W(8,:) = BiCubic(y,x,vw,uw+2);pV(9) = img(vw+1,uw-1);W(9,:) = BiCubic(y,x,vw+1,uw-1);pV(10) = img(vw+1,uw);W(10,:) = BiCubic(y,x,vw+1,uw);pV(11) = img(vw+1,uw+1);W(11,:) = BiCubic(y,x,vw+1,uw+1);pV(12) = img(vw+1,uw+2);W(12,:) = BiCubic(y,x,vw+1,uw+2);pV(13) = img(vw+2,uw-1);W(13,:) = BiCubic(y,x,vw+2,uw-1);pV(14) = img(vw+2,uw);W(14,:) = BiCubic(y,x,vw+2,uw);pV(15) = img(vw+2,uw+1);W(15,:) = BiCubic(y,x,vw+2,uw+1);pV(16) = img(vw+2,uw+2);W(16,:) = BiCubic(y,x,vw+2,uw+2);Value = 0;for i=1:16Value = Value + pV(i)*W(i,1)*W(i,2);end
endfunction W = BiCubic(y,x,yi,xi)W = zeros(1,2);a = -0.5;distX = abs(x-xi);if(distX <=1)W(1) = (a+2)*distX^3-(a+3)*distX^2+1;elseif(distX > 1 && distX <2)W(1) = a*distX^3-5*a*distX^2+8*a*distX-4*a;elseW(1) = 0;enddistY = abs(y-yi);if(distY <=1)W(2) = (a+2)*distY^3-(a+3)*distY^2+1;elseif(distY > 1 && distY <2)W(2) = a*distY^3-5*a*distY^2+8*a*distY-4*a;elseW(2) = 0;end
end

http://chatgpt.dhexx.cn/article/pEcBUdhI.shtml

相关文章

matlab 给图像双三次,图像灰度的双三次插值的MATLAB实现

matlab 给图像双三次,图像灰度的双三次插值的MATLAB实现

相比C/C实现&#xff0c;图像灰度的双三次插值的MATLAB实现要方便的多&#xff0c;下面是MATLAB语言实现 clc,clear; ffimread(C:\Program Files\MATLAB\R2013a\bin\work\lena.bmp); [mm,nn]size(ff);%将图像隔行隔列抽取元素&#xff0c;得到缩小的图像f mmm/2;nnn/2; fzeros(…
阅读更多...
java 双三次线性插值_三种常见的图像处理双三次插值算法

java 双三次线性插值_三种常见的图像处理双三次插值算法

三种常见的图像处理双三次插值算法 双立方插值计算涉及16像素，间(i’, j’)像中的包括 小数部分的像素坐标。dx表示X方向的小数坐标。dy表示Y方向的小数坐标。 详细 能够看下图： 依据上述图示与双立方插值的数学表达式能够看出。双立方插值本质上图像16个像素点 权重卷积之和…
阅读更多...
双三次插值 python实现_Python：用GPU实现双三次插值

双三次插值 python实现_Python：用GPU实现双三次插值

它不是GPU(而是尝试利用线程和CPU的向量单元)&#xff0c;但是pyvips比scipy快很多&#xff0c;您可以测试一下。在 我做了个基准&#xff1a;import sys import time import scipy.ndimage import pyvips scale 10 n_loops 10 start time.time() test_image scipy.ndimage…
阅读更多...
双三次插值及Matlab实现

双三次插值及Matlab实现

双三次插值及Matlab实现 一、简单实例 采用简单实例进行对双三次插值的介绍&#xff0c;由于双三次插值对于目标图像的某一像素进行估计时&#xff0c;所采用的像素信息为其周围16个像素点信息&#xff0c;因此不同于最近邻插值和双线性插值&#xff0c;此时假设有 5 5 5\tim…
阅读更多...
【opencv】最近邻插值、双线性插值、双三次插值（三次样条插值）

【opencv】最近邻插值、双线性插值、双三次插值（三次样条插值）

目录 1. 最近邻插值2. 双线性插值1&#xff09;简单理解2&#xff09;一般性 3. 双三次插值&#xff08;三次样条插值&#xff09;总结 b站 视频讲解 &#xff1a; https://www.bilibili.com/video/BV1wh411E7j9/ 1. 最近邻插值 举个简单例子&#xff1a;一个 3 3 3 \times 3…
阅读更多...
挑战图像处理100问（27）——双三次插值

挑战图像处理100问（27）——双三次插值

当我们需要对图像进行放大或缩小时&#xff0c;为了避免图像变形或失真&#xff0c;我们需要进行插值。插值是一种基于已知数据点&#xff0c;在这些数据点之间进行估计的方法。在图像处理中&#xff0c;常见的插值方法包括最邻近插值、双线性插值、双三次插值等。 双三次插值…
阅读更多...
【图像超分辨（SR）】通俗直观彻底理解双线性插值、双三次插值及其作用

【图像超分辨（SR）】通俗直观彻底理解双线性插值、双三次插值及其作用

写在前面的一点话 网上讲解基本双线性插值、双三次线性插值的文章很多&#xff0c;但大部分都是只在讲为什么是这样&#xff0c;并不算非常通俗&#xff08;起码对我来说需要额外查很多资料来补充理解&#xff09;。很少有文章能够给初学者一些比较直观的理解&#xff0c;因此…
阅读更多...
插值法(最邻近，双线性，双三次）的原理及实现

插值法(最邻近，双线性，双三次）的原理及实现

插值法(最邻近&#xff0c;双线性&#xff0c;双三次&#xff09;的原理及实现 常用的插值方法有最邻近插值法、双现象插值法和双三次插值法等&#xff0c;主要用于图像的放大或缩小。 缩小图像&#xff08;或称为下采样&#xff08;subsampled&#xff09; 或降采样&#xf…
阅读更多...
c语言表达式优先级（）

c语言表达式优先级（）

阅读更多...
表示关系x =y =z的c语言表达式为________.,为表示关系x≥y≥z，应使用C语言表达式____。...

表示关系x =y =z的c语言表达式为________.,为表示关系x≥y≥z，应使用C语言表达式____。...

为表焦距决定了画面的透视关系。 示关使用GREGRE ≥y≥桡神经沟位于 应C语言表关于脊柱正确的描写是() 建筑物或者其他设施以及建筑物上的搁置物、达式悬挂物发生( )造成他人损害的&#xff0c;所有人或者管理人应当承担民事责任,但能够证明自己没有过错的除外。 为表成对的脑颅…
阅读更多...
C语言运算表达式整理

C语言运算表达式整理

C语言的运算规则是按照运算符的优先级进行的&#xff0c;所以我们首先看一下C的运算优先级别 总结 最简单的优先级就是 算数运算符>关系运算符>逻辑运算符>赋值运算符 然后我们还要了解一个短路规则&#xff08;特性&#xff09; 短路规则&#xff1a;在整个逻辑表…
阅读更多...
与数学式子对应的C语言表达式是(),与数学式子3乘以x的n次方/（2x-1）对应的C语言表达式是...

与数学式子对应的C语言表达式是(),与数学式子3乘以x的n次方/（2x-1）对应的C语言表达式是...

满意答案 lengwei241 2013.03.25 采纳率：43% 等级：13 已帮助：11778人 18 与数学式子3乘以x的n次方/(2x-1)对应的C语言表达式是 3*x^n/(2*x-1) 3*x**n/(2*x-1) 3*pow(x,n)*(1/(2*x-1)) 3*pow(n,x)/(2*x-1) 答案是3*pow(x,n)*(1/(2*x-1)) 为什么 解答：其中pow(x,n)为C语言…
阅读更多...
C语言表达式和表达式的值

C语言表达式和表达式的值

今天突然发现如果能很好的理解表达式和表达式的值的概念&#xff0c;可以使编程代码变的更整洁。很多时候我们总是忘记从最基本的概念开始考虑问题。我觉得我们有必要把C/C标准看下&#xff0c;在里面肯定有很多我们一直困惑的问题的答案。 C语言是基于结构化程序设计思想的程序…
阅读更多...
以下c语言表达式与代数式计算结果,设有定义：float a=2,b=4,h=3；，以下C语言表达式中与代数式计算结果不相符的是...

以下c语言表达式与代数式计算结果,设有定义：float a=2,b=4,h=3；，以下C语言表达式中与代数式计算结果不相符的是...

设有定义：float a=2,b=4,h=3；，以下C语言表达式中与代数式计算结果不相符的是 设有式计算结Women in Britain, having some qualifications, were enfranchised until ______. 定义达式代数The usual rhyme scheme for the English or Shakespearean sonnet is( ). In “For …
阅读更多...
与数学式对应的c语言表达式为,数学表达式“|x|4”对应的C语言表达式是“x-4||x4”。...

与数学式对应的c语言表达式为,数学表达式“|x|4”对应的C语言表达式是“x-4||x4”。...

数学表达式“|x|4”对应的C语言表达式是“x-4||x4”。 数学式《莺莺传》故事的时代为( ) 表达人力资本的投资是提高技术水平的必要途径。() 对达式教育投资是人力资本的投资唯一重点。() 微商是以移动终端为载体&#xff0c;应的C语言表通过社交媒介手段&#xff0c;进行传播的…
阅读更多...
C语言 运算符、表达式

C语言 运算符、表达式

运算符、表达式 1、 C语言运算符 算术运算符和算术表达式 &#xff08;加&#xff09;、—&#xff08;减&#xff09;、*&#xff08;乘&#xff09;、/&#xff08;除&#xff09;、%&#xff08;取余&#xff0c;也叫模运算符&#xff0c;该运算符两侧都要求为整数&#xff…
阅读更多...
c语言表达式语法问题,c语言表达式语法规则是什么_后端开发

c语言表达式语法问题,c语言表达式语法规则是什么_后端开发

c语言统计单词个数的方法_后端开发 在一篇文章中单词都是用空格隔开的&#xff0c;所以单词个数空格数1&#xff0c;c语言统计单词个数实际上转换成了统计文章中的空格数&#xff0c;可以用while和if来进行统计。 c语言表达式语法规则是什么 C语言表达式语法规则如下&#xff1…
阅读更多...
c语言表达式成立,若有int y;则表示命题“y是偶数”成立的c语言表达式是多少...

c语言表达式成立,若有int y;则表示命题“y是偶数”成立的c语言表达式是多少...

满意答案 hoome_09 2017.12.28 采纳率&#xff1a;44% 等级&#xff1a;8 已帮助&#xff1a;263人 1. 若有int y&#xff1b;则表示命题“y是奇数”成立的C语言表达式是 (y%2 1) 。 2. 在C语言中&#xff0c;表示逻辑“真”值用(true) 表示。 3. 条件“2&#xff1c;x&…
阅读更多...
C语言表达式用法快来看看

C语言表达式用法快来看看

点击上方蓝字关注我&#xff0c;了解更多咨询 表达式是C语言的主体。在C语言中&#xff0c;表达式由操作符和操作数组成。最简单的表达式可以只含有一个操作数。根据表达式所含操作符的个数&#xff0c;可以把表达式分为简单表达式和复杂表达式两种&#xff0c;简单表达式是只含…
阅读更多...
数学式子对应的c语言表达式是,把数学式写成C语言表达式

数学式子对应的c语言表达式是,把数学式写成C语言表达式

(1) 3.26*exp(x)1.0/3.0*pow((ab), 4) (2) 2*sqrt(x)(ab)/(3.0*sin(x)) (3) g*m1*m2/(r*r) (4) double pi 3.14 2.0*pi*r pi*r*r cos(45.0*pi / 180.0 ) (5) loan * rate * pow( (1rate) , month ) / ( pow( (1rate) , month) - 1) 扩展资料&#xff1a; 指针&#xff1a; 如…
阅读更多...
推荐文章

Copyright @ 2022~2023