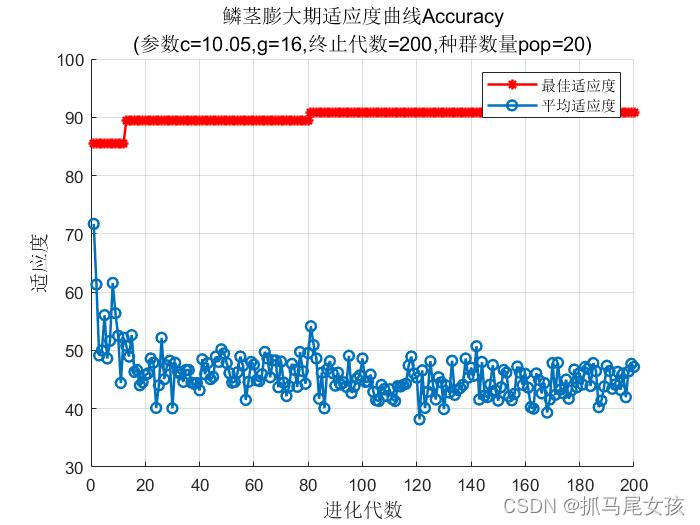
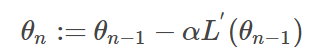更新一下:以下代码是优化高斯核函数的惩罚因子和g参数的。因为在svmtrain函数中没有给-v赋值,所以是默认值2,若要优化其他核函数,可以修改svmtrain中的-v参数的值以及增加其他参数的粒子更新代码。此代码的目标函数是svmtrain三折交叉验证返回的准确率,读者可根据实际情况做修改。
粒子群算法是模拟鸟群觅食过程中的迁徙和群集行为时提出的一种基于群体智能的优化算法。粒子群算法是一种随机全局优化技术,通过粒子间的相互作用发现复杂搜索空间中的最优区域。用粒子群算法优化支持向量机的结构参数,可以快速收敛寻得最优解,提高支持向量机的学习能力。在粒子群算法中,可以把所有的优化问题的解想象为D维搜索空间上的一个点,而这个点就是一个“粒子”。通过目标函数来评估当前粒子所处位置的好坏,得到相应的适应度值。在种群中粒子的随机初始化形成后,会按照某种方式进行迭代,直到终止条件符合要求,从而寻得最优解。
基于粒子群算法的支持向量机参数选择的具体步骤如下:
(1)设置待优化的惩罚因子C和核参数γ的取值范围,以及参数局部搜索能力、种群最大数量等其他初始化参数。
(2)在惩罚因子C和核参数γ的取值范围随机初始化一群粒子。初始化每个粒子的位置信息和速度信息,然后将每个粒子的历史最优位置[Pbest]_i设为当前位置,群体中最好粒子的当前位置设为Gbest。
(3)将样本数据的回归误差作为目标函数,计算每个粒子的适应度。
(4)对每个粒子,若其适应度值优于上一轮的历史最优值,就是当前位置取代历史最优位置,成为新的[Pbest]_i。
(5)对每个粒子,若其适应度值优于上一轮的全局最优适应度值,就用当前位置取代全局最优位置,成为新的Gbest。
(6)按照以下公式分别对粒子的速度和位置进行更新。
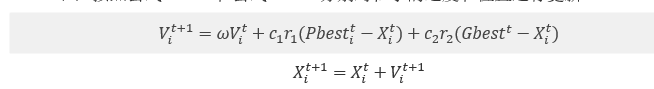
(7)判读是否满足终止条件,满足时则停止运算,否则返回步骤(3)继续迭代。
function [bestCVaccuarcy,bestc,bestg,pso_option] = psoSVMcgForClass(train_label,train,pso_option)
% psoSVMcgForClass
%% 参数初始化
if nargin == 2 %当输入两个参数时执行下面的语句pso_option = struct('c1',1.5,'c2',1.7,'maxgen',200,'sizepop',20, ...'k',0.6,'wV',1,'wP',1,'v',3, ...'popcmax',10^4,'popcmin',10^(-1),'popgmax',10^3,'popgmin',10^(-2));
end
% c1:初始为1.5,pso参数局部搜索能力
% c2:初始为1.7,pso参数全局搜索能力
% maxgen:初始为200,最大进化数量
% sizepop:初始为20,种群最大数量
% k:初始为0.6(k belongs to [0.1,1.0]),速率和x的关系(V = kX)
% wV:初始为1(wV best belongs to [0.8,1.2]),速率更新公式中速度前面的弹性系数
% wP:初始为1,种群更新公式中速度前面的弹性系数
% v:初始为3,SVM Cross Validation参数
% popcmax:初始为100,SVM 参数c的变化的最大值.
% popcmin:初始为0.1,SVM 参数c的变化的最小值.
% popgmax:初始为1000,SVM 参数g的变化的最大值.
% popgmin:初始为0.01,SVM 参数c的变化的最小值.Vcmax = pso_option.k*pso_option.popcmax;
Vcmin = -Vcmax ;
Vgmax = pso_option.k*pso_option.popgmax;
Vgmin = -Vgmax ;eps = 1e-1;%% 产生初始粒子和速度
for i=1:pso_option.sizepop% 随机产生种群和速度pop(i,1) = (pso_option.popcmax-pso_option.popcmin)*rand+pso_option.popcmin;pop(i,2) = (pso_option.popgmax-pso_option.popgmin)*rand+pso_option.popgmin;V(i,1)=Vcmax*rands(1,1);V(i,2)=Vgmax*rands(1,1);% 计算初始适应度cmd = ['-v ',num2str(pso_option.v),' -c ',num2str( pop(i,1) ),' -g ',num2str( pop(i,2) )];fitness(i) = svmtrain(train_label, train, cmd); %保存的是三折交叉验证的准确率fitness(i) = -fitness(i);
end% 找极值和极值点
[global_fitness bestindex]=min(fitness); % 全局极值 第一个是值 第二个是索引
local_fitness=fitness; % 个体极值初始化global_x=pop(bestindex,:); % 全局极值点
local_x=pop; % 个体极值点初始化% 每一代种群的平均适应度 零矩阵
avgfitness_gen = zeros(1,pso_option.maxgen); %% 迭代寻优
for i=1:pso_option.maxgenfor j=1:pso_option.sizepop%速度更新V(j,:) = pso_option.wV*V(j,:) + pso_option.c1*rand*(local_x(j,:) - pop(j,:)) + pso_option.c2*rand*(global_x - pop(j,:));%较大的ω使粒子更易跳出局部最优解,获得更强的全局寻优能力,但也会使效率降低,不宜收敛;较小的ω容易陷入局部最优解,但更易收敛。%c1=0时,为无私型粒子群算法,丧失群体多样性,容易陷入局部最优解。%c2=0时,为自私型粒子群算法,没有信息的社会共享,收敛速度减慢。%粒子最大速度:维护算法探索能力和开发能力的平衡。速度增大,粒子的探索能力增强,但容易飞过最优解。速度减小,开发能力较大,但容易陷入局部最优。if V(j,1) > VcmaxV(j,1) = Vcmax;endif V(j,1) < VcminV(j,1) = Vcmin;endif V(j,2) > VgmaxV(j,2) = Vgmax;endif V(j,2) < VgminV(j,2) = Vgmin;end%种群更新pop(j,:)=pop(j,:) + pso_option.wP*V(j,:);if pop(j,1) > pso_option.popcmaxpop(j,1) = pso_option.popcmax;endif pop(j,1) < pso_option.popcminpop(j,1) = pso_option.popcmin;endif pop(j,2) > pso_option.popgmaxpop(j,2) = pso_option.popgmax;endif pop(j,2) < pso_option.popgminpop(j,2) = pso_option.popgmin;end% 自适应粒子变异if rand>0.5k=ceil(2*rand);if k == 1pop(j,k) = (20-1)*rand+1;endif k == 2pop(j,k) = (pso_option.popgmax-pso_option.popgmin)*rand + pso_option.popgmin;endend%适应度值cmd = ['-v ',num2str(pso_option.v),' -c ',num2str( pop(j,1) ),' -g ',num2str( pop(j,2) )];fitness(j) = svmtrain(train_label, train, cmd);fitness(j) = -fitness(j);cmd_temp = ['-c ',num2str( pop(j,1) ),' -g ',num2str( pop(j,2) )];model = svmtrain(train_label, train, cmd_temp);if fitness(j) >= -65continue;end%个体最优更新if fitness(j) < local_fitness(j)local_x(j,:) = pop(j,:);local_fitness(j) = fitness(j);endif abs( fitness(j)-local_fitness(j) )<=eps && pop(j,1) < local_x(j,1)local_x(j,:) = pop(j,:);local_fitness(j) = fitness(j);end%群体最优更新if fitness(j) < global_fitnessglobal_x = pop(j,:);global_fitness = fitness(j);endif abs( fitness(j)-global_fitness )<=eps && pop(j,1) < global_x(1)global_x = pop(j,:);global_fitness = fitness(j);endendfit_gen(i) = global_fitness;avgfitness_gen(i) = sum(fitness)/pso_option.sizepop;
end%% 结果分析
figure;
hold on;
plot(-fit_gen,'r*-','LineWidth',1.5);
plot(-avgfitness_gen,'o-','LineWidth',1.5);
legend('最佳适应度','平均适应度',3);
xlabel('进化代数','FontSize',12);
ylabel('适应度','FontSize',12);
grid on;bestc = global_x(1);
bestg = global_x(2);
bestCVaccuarcy = -fit_gen(pso_option.maxgen);line1 = '适应度曲线Accuracy[PSOmethod]';
line2 = ['(参数c1=',num2str(pso_option.c1), ...',c2=',num2str(pso_option.c2),',终止代数=', ...num2str(pso_option.maxgen),',种群数量pop=', ...num2str(pso_option.sizepop),')'];
% line3 = ['Best c=',num2str(bestc),' g=',num2str(bestg), ...
% ' CVAccuracy=',num2str(bestCVaccuarcy),'%'];
% title({line1;line2;line3},'FontSize',12);
title({line1;line2},'FontSize',12);
效果图如下