1. 概述

重点

转发表和流表是如何计算、维护和安装的。

路由器的转发操作需要根据转发表将输入分组传输到合适的输出链路，因此转发表的初始化和更新很重要。有两种方式能够完成转发表的计算、维护与安装：

路由器控制：每台路由器都运行一种路由选择算法。
①路由器包含转发和路由选择两种功能。
②路由器通过路由选择组件间的通信计算转发表。
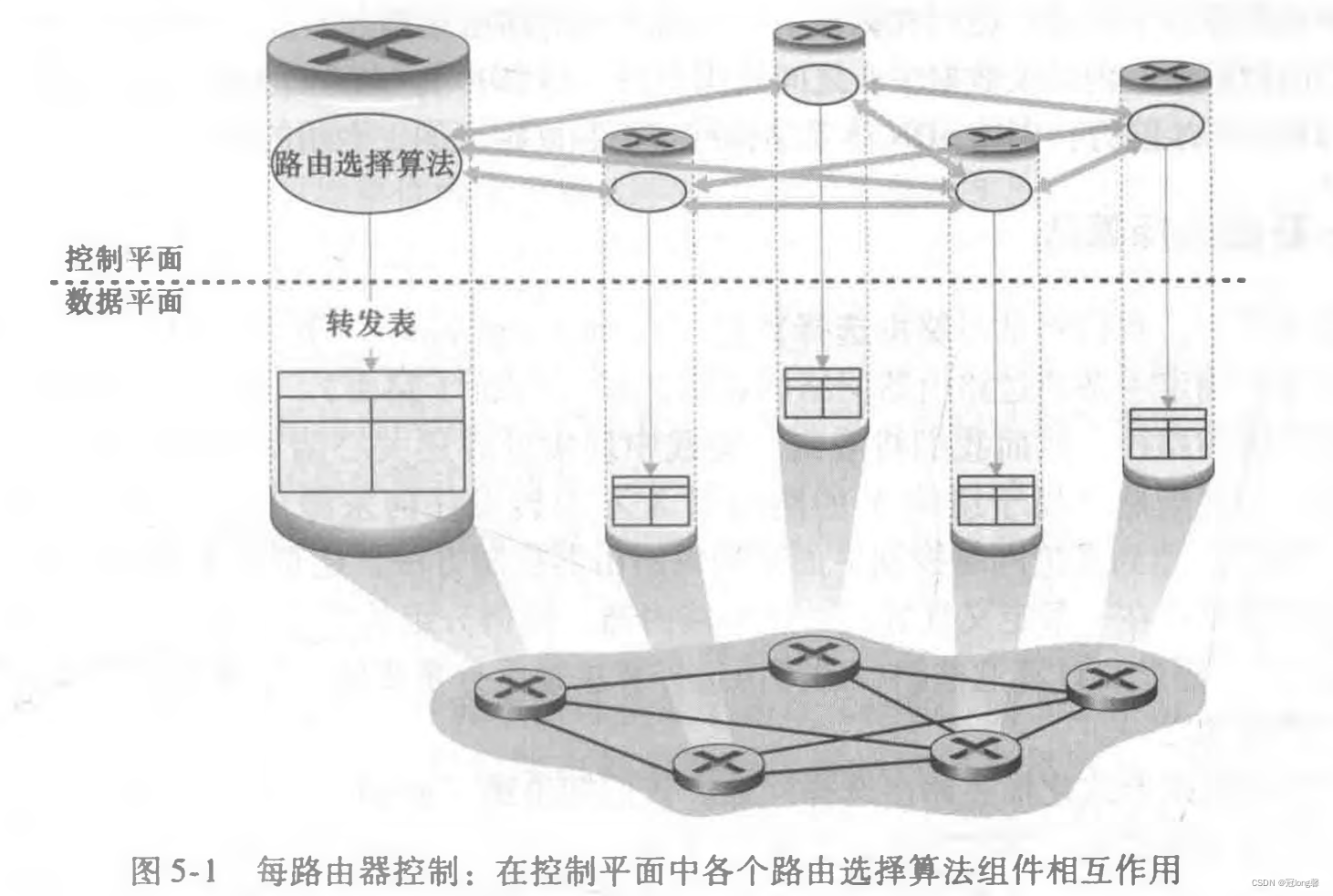
逻辑集中式控制：逻辑集中式控制器计算分发转发表。
①路由器仅执行转发功能。
②路由器中有一个控制代理（CA）以配置和管理路由器的转发表。

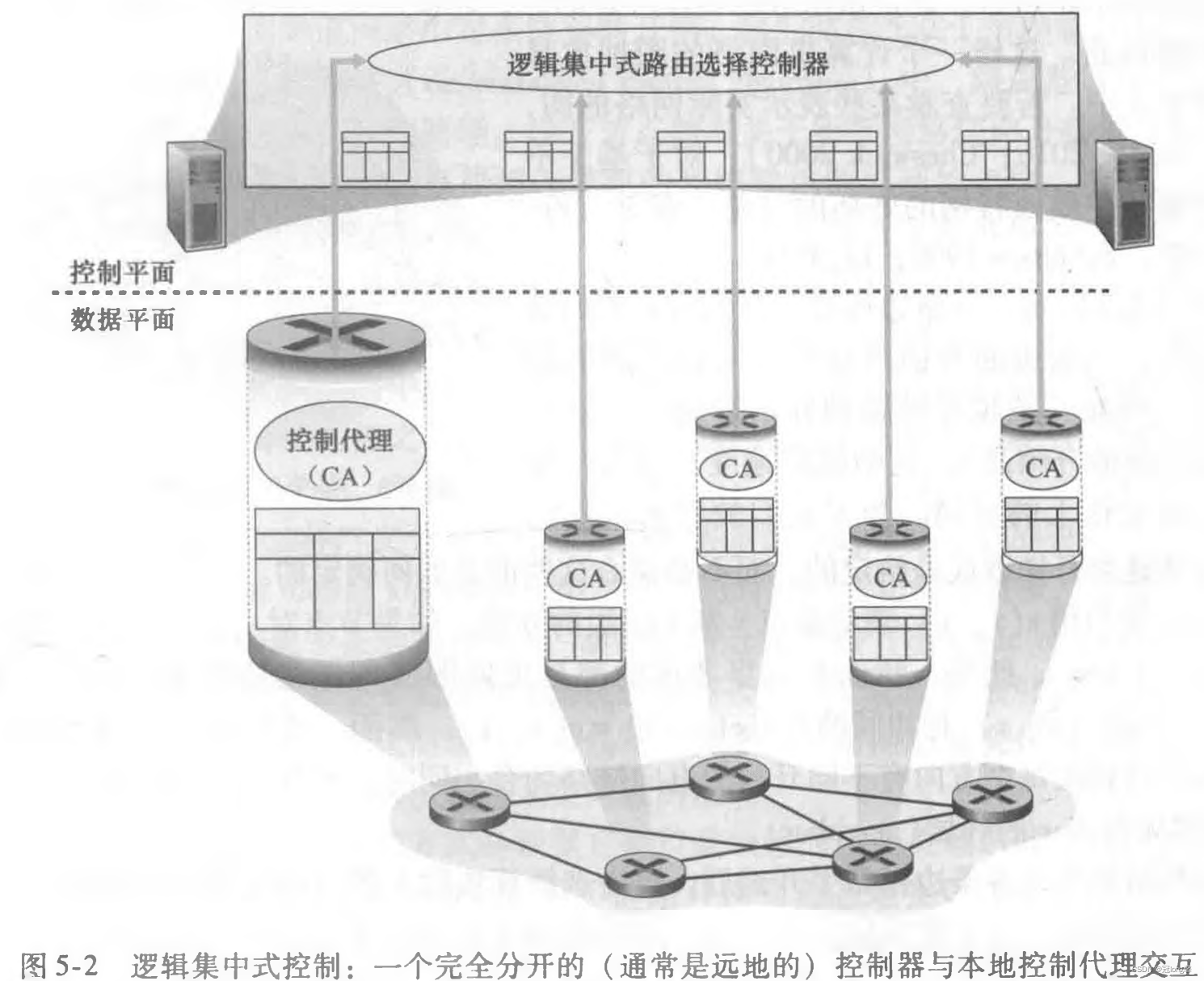
两种工作方式中路由器分别含有路由选择组件和控制代理，但是它们的功能是完全不同的。两种方式的关键差异：

路由选择组件可以相互交互，也可以主动参与转发表的计算。
控制代理CA既不能相互交互，也不能主动参与转发表的计算。

2. 路由选择算法

路由选择算法是为从源到目的的分组确定一条开销最小的路由，通过计算源到目的的最短路径计算转发表。常见的路由算法有以下分类：

集中式路由选择算法：利用全局的网络知识计算从源到目的的最短路径及开销。
①以所有节点的连通性和链路的开销为输入。
②常见算法：LS
分散式路由选择算法：路由器以迭代、分布式的方式计算最短路径及其开销。
①以直接相连的邻居节点及其链路开销为输入。
②常见算法：DV

静态路由选择算法：人为手工配置转发表。
①路由更新慢、优先级高。
动态路由选择算法：利用路由选择算法计算更新转发表。
①路由更新快、及时响应链路费用和网络拓扑变化。

2.1 链路状态路由选择算法（LS）

（1）定义
LS是一种集中式路由选择算法，它以网络拓扑和所有链路的开销为输出。

广播链路状态分组：每个节点向其他节点广播链路状态分组，链路状态分组由节点连接链路的标识和开销组成。
Dijstra算法：采用Dijstra算法计算源到目的的最短路径和开销。
①思路：每次选择距离源节点开销最小的未被访问的节点加入最短路径，然后对其邻接且还未被访问的节点的开销进行更新。算法结束后，每个节点都有一个前驱节点，可以通过前驱节点得到源到目的的最短路径。

②每个节点的转发表中保存源到目的的最短路径上的下一条节点。

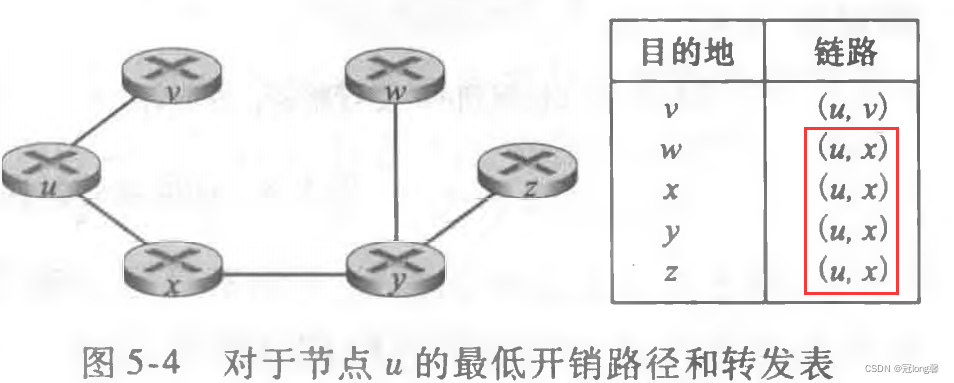
（2）问题

震荡现象：假设链路开销表示链路负载。
因为链路开销动态的变化导致路由表更新频繁，在环形链路中分组可能无法到达目的地。
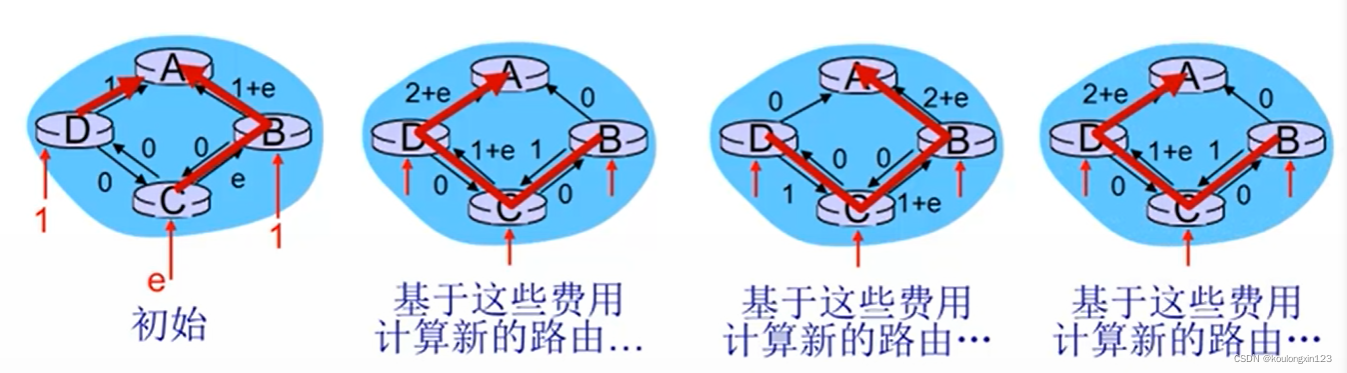
解决方法
①强制链路开销不依赖链路负载（×）：因为路由选择需要确保避开高度拥塞的链路。
②确保并不是所有路由器都运行LS算法（√）

2.2 距离向量路由选择算法（DV）

距离向量算法是一种迭代的、异步的和分布式的算法。
（1）定义

Bellman-Ford方程： $d_x(y)=\min\{c(x,v)+d_v(y)\}$
① $d_x(y)$ 表示x到y最低开销路径的费用。
②节点x到节点y的开销可以通过节点x到邻居节点的开销和邻居节点到节点y的开销表示。因此当邻居节点的距离向量不再更新，且邻居与节点x的开销没有变化时，节点x到达y的最低开销路径的费用不会发生改变。
距离向量（DV）算法：采用Bellman-Ford方程迭代的、异步的、分布式的更新节点的距离向量，计算获得转发表项。
①思路：当节点发现与之直接相连链路的开销变化或接收到邻居的距离向量更新时，它就去计算更新距离向量。如果距离向量发生改变，则向所有邻居发送这个更新的距离向量。
②步骤：等待（直接相连链路开销变化、收到邻居距离向量的更新）–>重新计算距离向量–>如果DV发生变化，则通知所有邻居。

（2）特点

异步迭代：不要求所有节点操作一致，仅当直接相连的链路开销发生改变或收到邻居的DV更新时，才会引发局部迭代的。
分布式：DV算法不需要全局信息，通过采用Bellman-Ford算法，利用邻居DV计算更新距离向量。当DV发生变化时才通告给邻居。

DV算法中有两个能够引起局部迭代的因素：直接相连链路开销变化、收到邻居DV更新。当直接相连的链路开销变化时，可能引起链路故障。

（3）问题

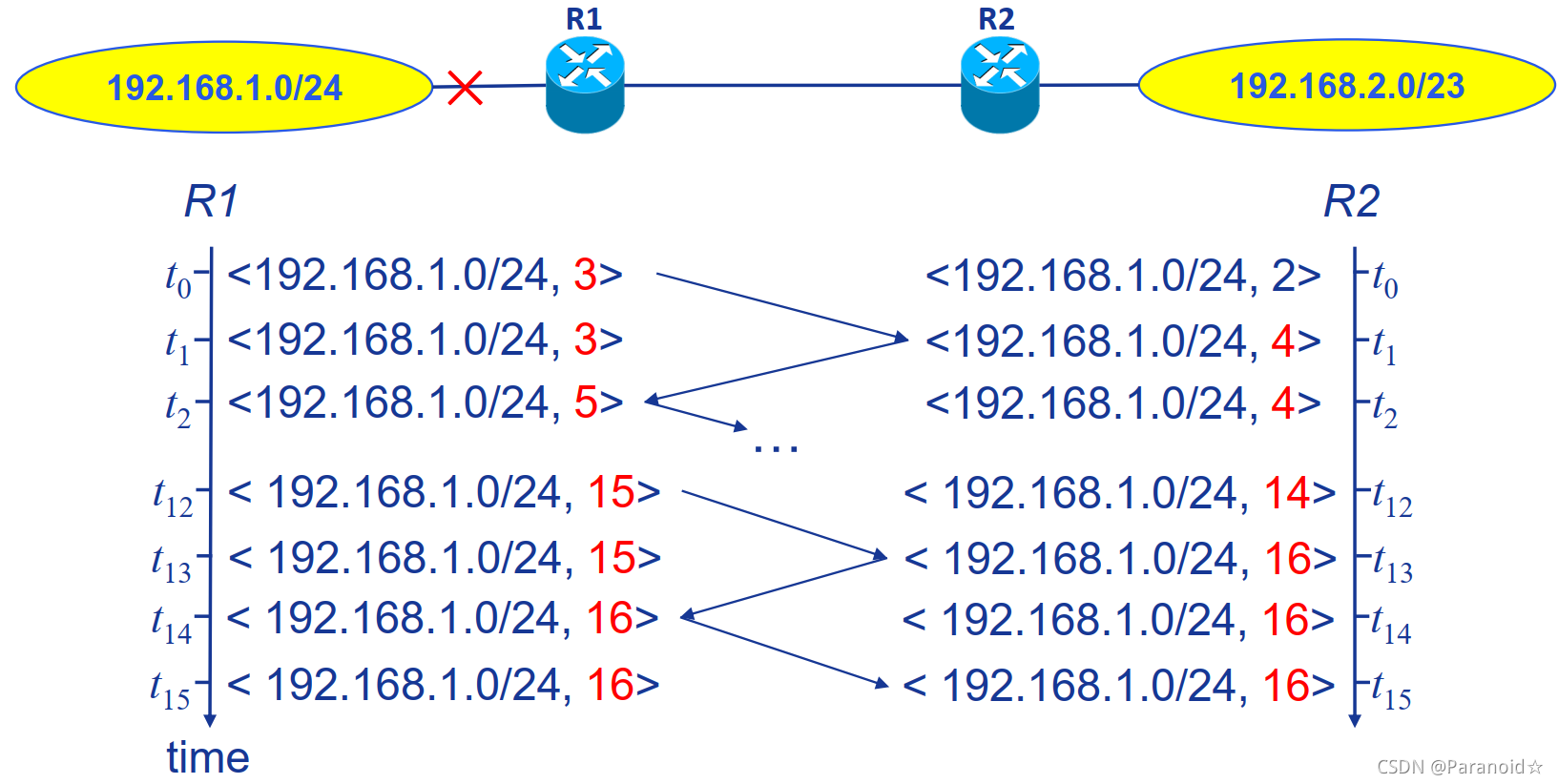
无穷计数问题：链路开销增大的坏消息传播的很慢。
①现象：z需要通过y路由才能到达x，当x与y相连的链路开销增大时，会引发节点y的局部迭代。这种情况下会形成选择环路，即为了到达x，y需要通过z的路由，z需要通过y路由。这种情况下DV的更新会导致多次迭代。

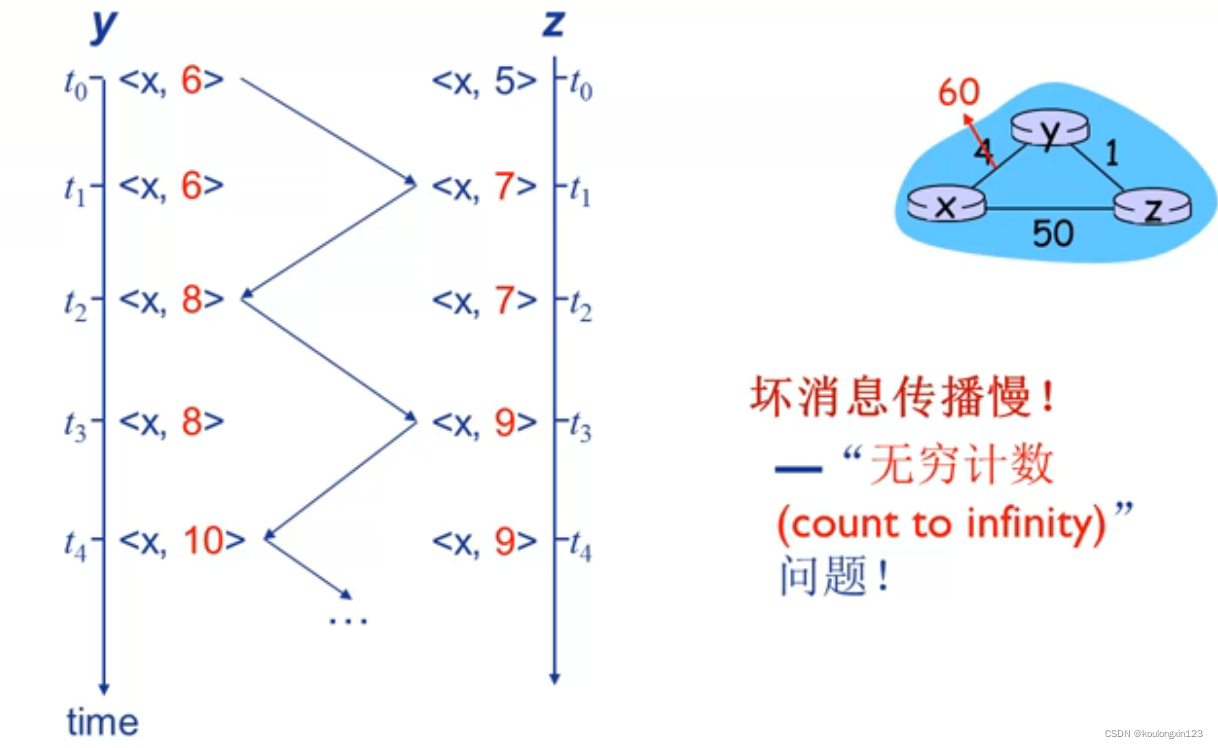
为了解决无穷计数问题，可以采用毒性逆转的方法解决。

毒性逆转：如果一个节点Z到达目的节点X的最短路径是通过某个邻居Y，则Z通知给邻居节点Y到达目的X的距离为无穷大。

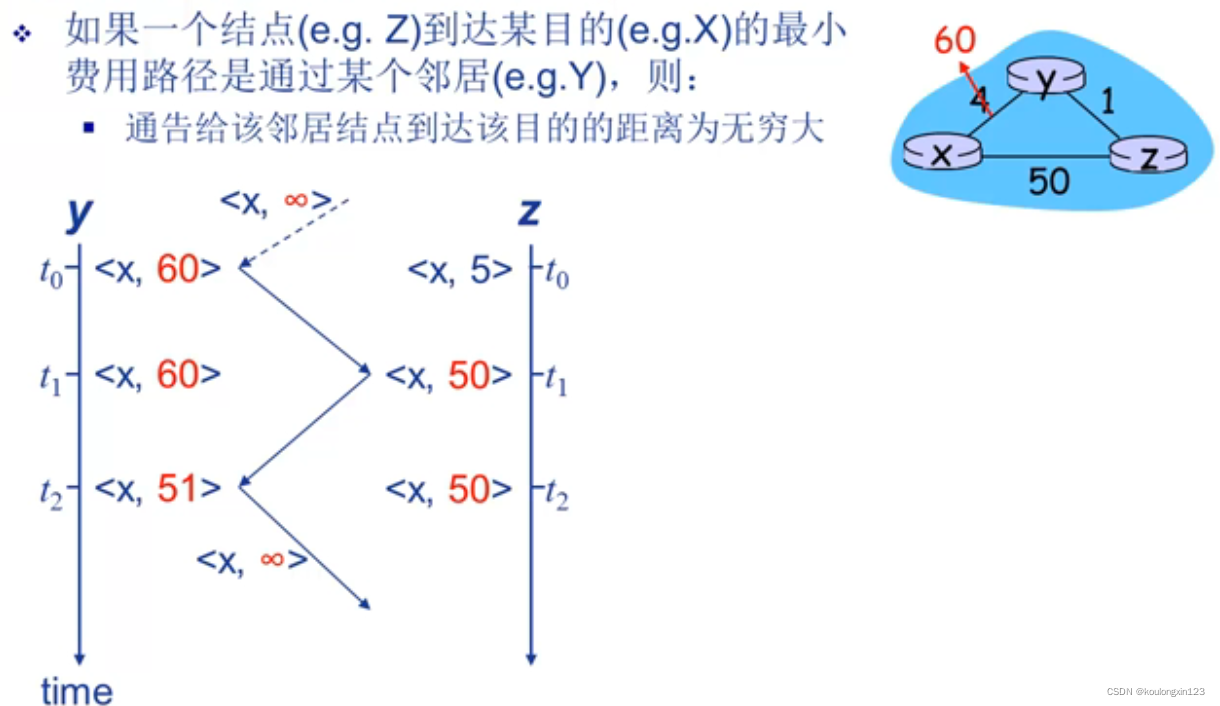
①局限：当涉及到3个或更多节点的环路将无法使用毒性逆转技术检测到。

2.3 DV和LS算法的对比

全局与离散：LS需要全局信息，每个节点需要与其他所有节点通信。DV不需要全局信息，只需要根据直接相连链路的开销和邻居节点的DV计算更新DV。
报文复杂性：采用LS算法时，任何一条链路开销发生变化都需要通知其他所有节点。采用DV算法时，仅当系欸但那距离向量发生变化时才需要通知所有邻居节点。
收敛速度：DV算法时间复杂度为 $O(|V|^2)$ ，LS算法时间复杂度为 $O (∣ V ∣ ∣ E ∣)$ 。
健壮性：LS算法各个节点路由计算是分离的，具有健壮性。DV算法一个不正确的节点值会扩散到整个网络。

本节中我们介绍了路由选择算法的概念以及两种主要的路由选择算法。路由选择算法的作用是在路由器控制转发表的计算、维护时计算并更新路由表表项。传统的路由选择算法可以划分为静态路由选择和动态路由选择，其中静态路由选择算法是由人工配置路由表项，路由更新慢但优先级高。路由选择算法也可以分为集中式路由选择算法和分散式路由选择算法。集中式路由选择算法如LS需要全局信息，每个节点需要与其他所有节点通信。无论合适链路开销发生变化，都需要向所有节点发送新的链路开销。分散式路由选择算法如DV不需要全局信息，它根据直接相连的链路开销和邻居节点DV计算节点的距离向量。当DV发生变化时需要向邻居发送DV更新。通过异步迭代、分布式的更新实现了路由表表项的计算与维护。LS算法通过Dijkstra算法计算更新路由表，但是可能存在震荡问题。DV算法通过Bellman-Ford方程实现通过直接相连的链路开销和邻居DV计算并更新转发表，但具有无穷计数的问题，可以采用毒性逆转解决。