一、栈

1.栈的概念及结构栈

一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。不同于我们所说的栈区，栈是一种数据结构，栈区是操作系统的内容。

进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵守后进先出的原则。

压栈：栈的插入操作叫做入栈，入数据在栈顶。

出栈：栈的删除操作叫做出栈，出数据也在栈顶。

相当于只能尾插尾删的顺序表

2.栈的实现

栈的实现一般可以使用数组或者链表实现，相对而言数组的结构实现更优一些，因为数组在尾上插入数据的代价比较小。

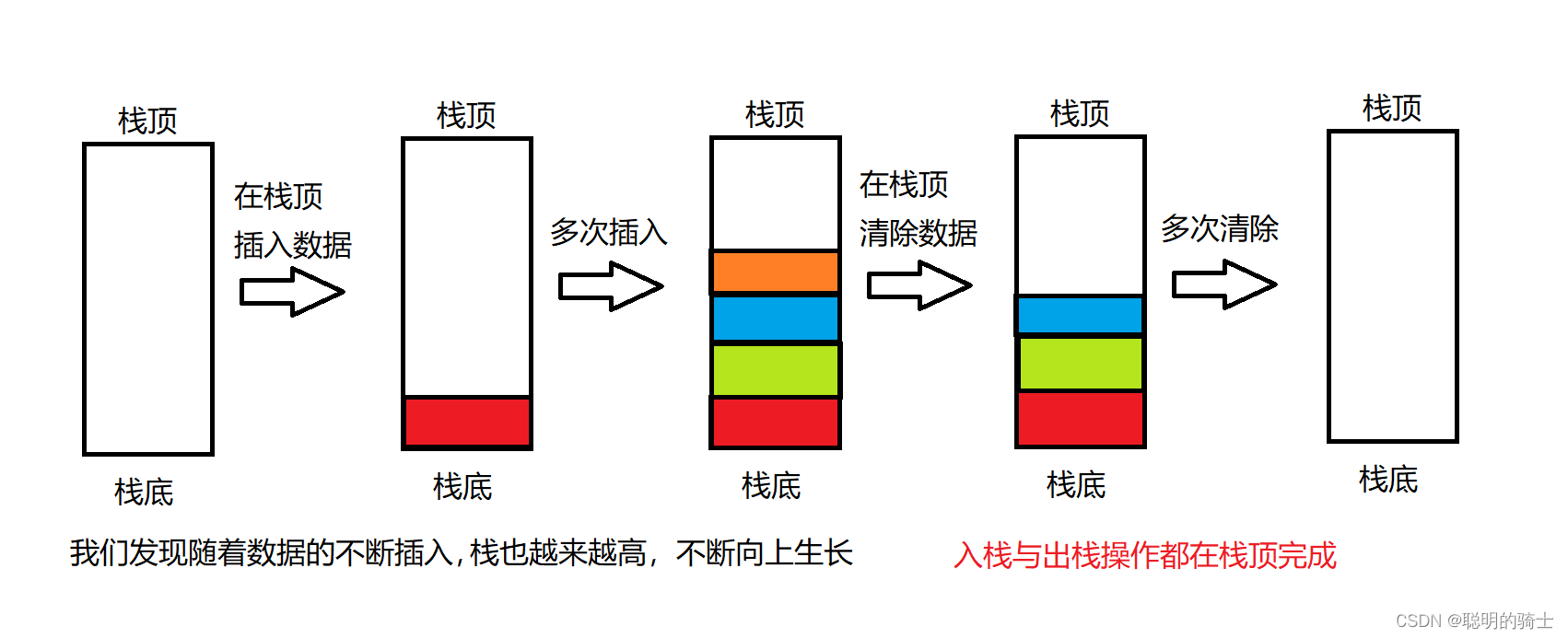
这里只需要完全使用顺序表的增删查改的操作函数即可，包括：顺序表的初始化，扩容，尾插，尾删，判空，元素个数等，但是注意栈中的元素被使用后会立刻出栈。

stack.h

#define TYPE int
typedef struct stackzone
{TYPE* arr;int volume;int top;//top是栈顶的元素编号，相当于size（不是下标）
}stack;//初始化栈
void initstack(stack* p);//扩容
void enlarge(stack* p);//栈只能尾插数据，插入数据
void stackpush(stack* p, TYPE x);//栈也只能尾删数据，删除数据
void stackpop(stack* p);//找到栈顶的元素
TYPE stacktop(stack* p);//判断栈是否为空
bool stackempty(stack* p);//判断栈中元素的多少
int stacksize(stack* p);

stack.c

#include"stack.h"//初始化
void InitSeqlist(SList* p)
{assert(p);p->size = 0;p->volume = 0;p->SL = NULL;
}//销毁
void destory(SList* p)
{assert(p);free(p->SL);p->size = 0;p->volume = 0;p->SL = NULL;
}//扩容
void enlarge(SList* p)
{if (p->size == p->volume)//容量与数据量相同扩容，每次扩容当前二倍大小的空间{assert(p);int newvolume = (p->volume == 0 ? 4 : 2 * p->volume);//定义一个变量保存新容量的大小，容量为0扩容4个，不为0扩容二倍TYPE* p1 = (TYPE*)realloc(p->SL, newvolume*sizeof(TYPE));//容量为0时，malloc与realloc效果相同if (p1 == NULL){perror("realloc");return;}p->SL = p1;p->volume = newvolume;}
}void Seqlist_back_push(SList* p, TYPE a)
{assert(p);enlarge(p);//函数负责在适当时负责扩容*((p->SL) + (p->size)) = a;//此时size正好是应插入位置的下标p->size++;//size 自增
}void Seqlist_front_push(SList* p, TYPE a)
{assert(p);enlarge(p);//函数负责在适当时负责扩容int i = p->size;while (i >= 0){p->SL[i] = p->SL[i - 1];//顺序表的头插需要将所有数据从后向前后挪一位i--;}*(p->SL) = a;//插入数据p->size++;//自增
}void Seqlist_back_pop(SList* p)
{assert(p);p->size--;//只需要减少有效数据的个数，自减即可
}void Seqlist_front_pop(SList* p)
{assert(p);int i = 0;for (i = 0; i < p->size - 1; i++){p->SL[i] = p->SL[i + 1];//把每一个数据从前向后挪一位}p->size--;
}void print(SList* p)
{assert(p);int i = 0;for (i = 0; i < p->size; i++){printf("%d ", p->SL[i]);}printf("\n");
}int Seqlist_search_element(SList* p, TYPE a)
{assert(p);int i = 0;for (i = 0; i < p->size; i++){if (p->SL[i] == a){return i;//找到了返回下标}}return -1;//找不到返回-1
}void Seqlist_modify_element(SList* p, size_t pos, TYPE b)
{p->SL[pos] = b;//改变某个下标对应的数据
}//顺序表在pos位置插入a
void Seqlist_insert_element(SList* p, int pos, TYPE a)//包括pos从后向前后挪一位再赋值
{assert(p);assert(pos < (p->size));enlarge(p);int i = pos;for (i = pos; i < p->size; i++){p->SL[i + 1] = p->SL[i];}p->SL[pos] = a;p->size++;
}//顺序表删除pos位置的值
void Seqlist_delete_element(SList* p, int pos)
{int i = 0;for (i = pos; i < p->size - 1;i++){p->SL[i] = p->SL[i + 1];//从前向后覆盖pos后的数据}p->size--;//自减
}

test.c

#include"stack.h"void test()
{
stack s;
stack* p = &s;
initstack(p);stackpush(p, 1);
stackpush(p, 2);
stackpush(p, 3);
stackpush(p, 4);
printf("%d\n",stacktop(p));//使用
stackpop(p);//出栈
printf("%d\n", stacktop(p));//使用
stackpop(p);//出栈
//栈在使用后就会删除
stackpop(p);
stackpop(p);
printf("%d\n",stacksize(p));stackdestory(p);}int main()
{
test();
return 0;
}

二、队列

1.队列的概念及结构队列

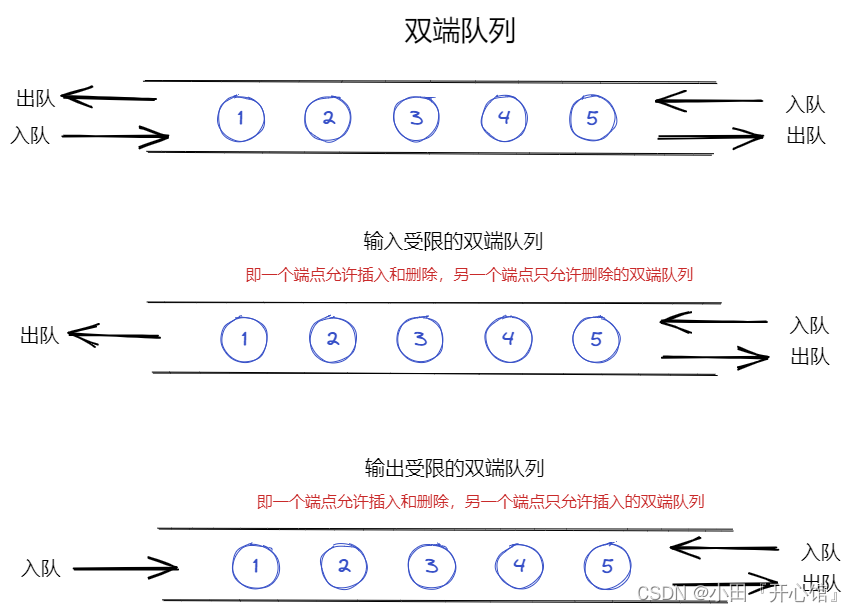
只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列中数据具有先进先出入的性质。

就像排队一样，有一群人在银行柜台前排队，有的办完业务离开了，就相当于出队列；又有的人在后面加入排队，相当于入队列，一头进一头出。

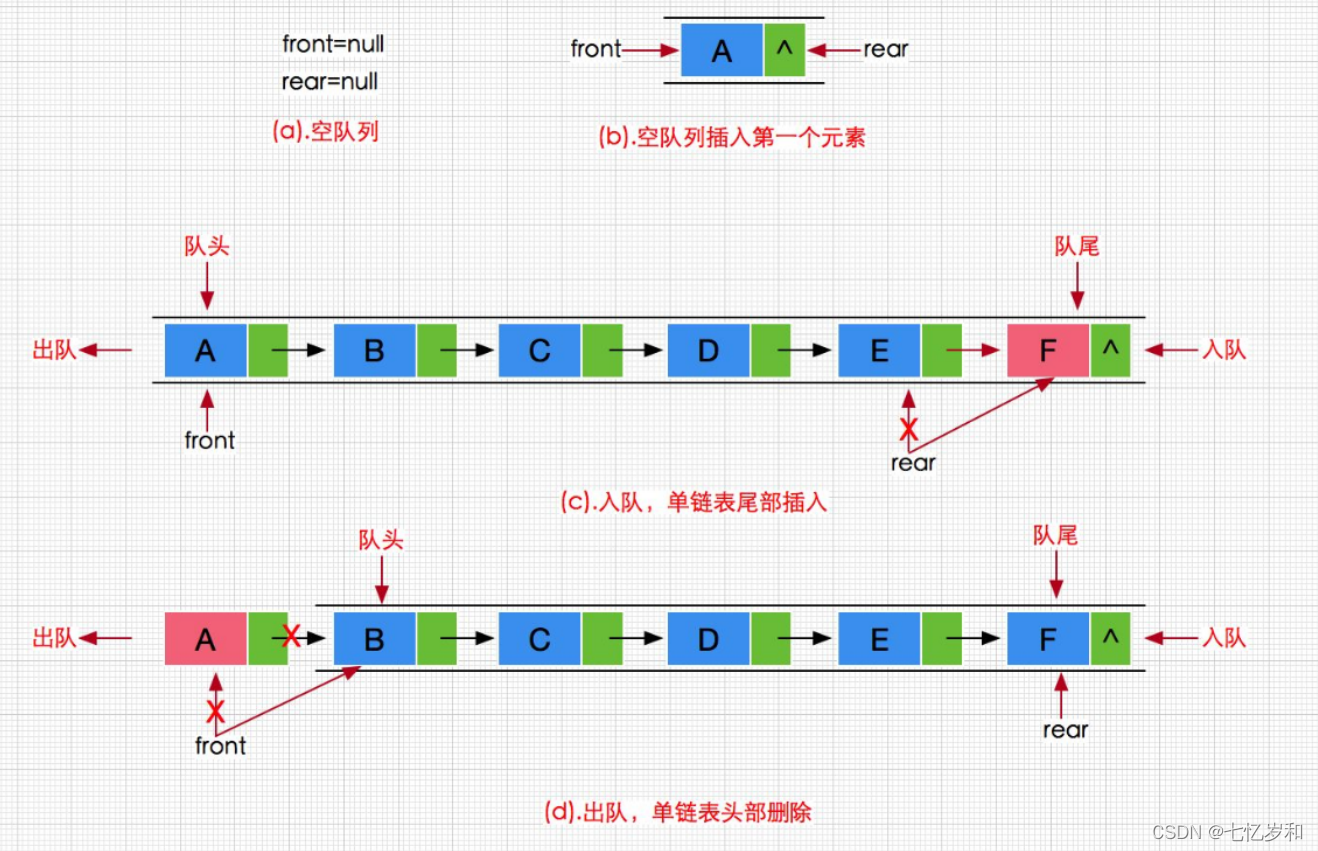
入队列：进行插入操作的一端称为队尾，将数据尾插即为入队列。

出队列：进行删除操作的一端称为队头，在队头删除数据即为出队列。

2.队列的实现

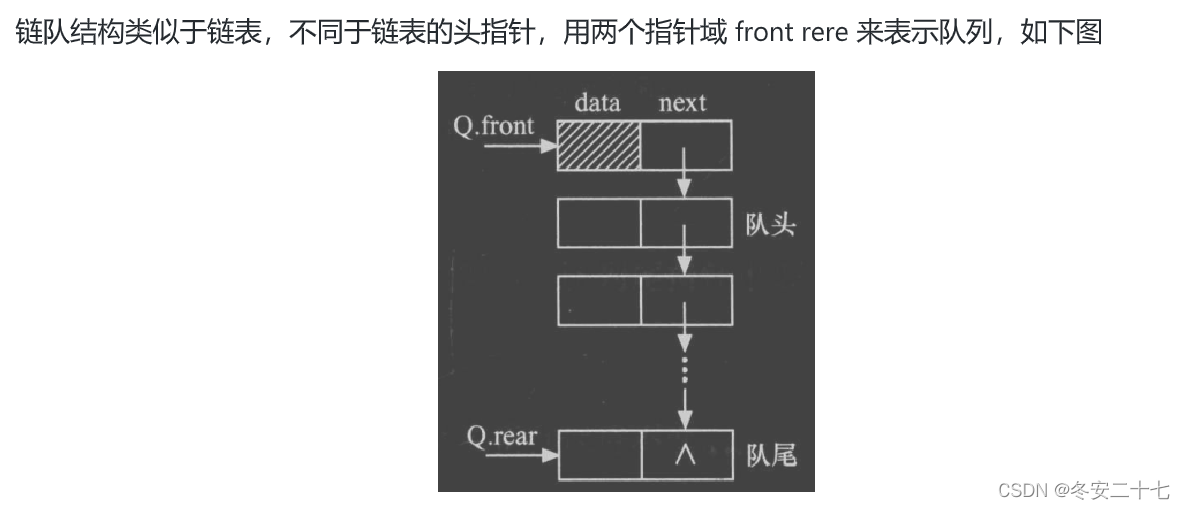
队列的实现队列可以数组或链表的结构实现，使用链表的结构实现更优一些，因为如果使用数组的结构，出队列在数组头上出数据，效率会比较低。

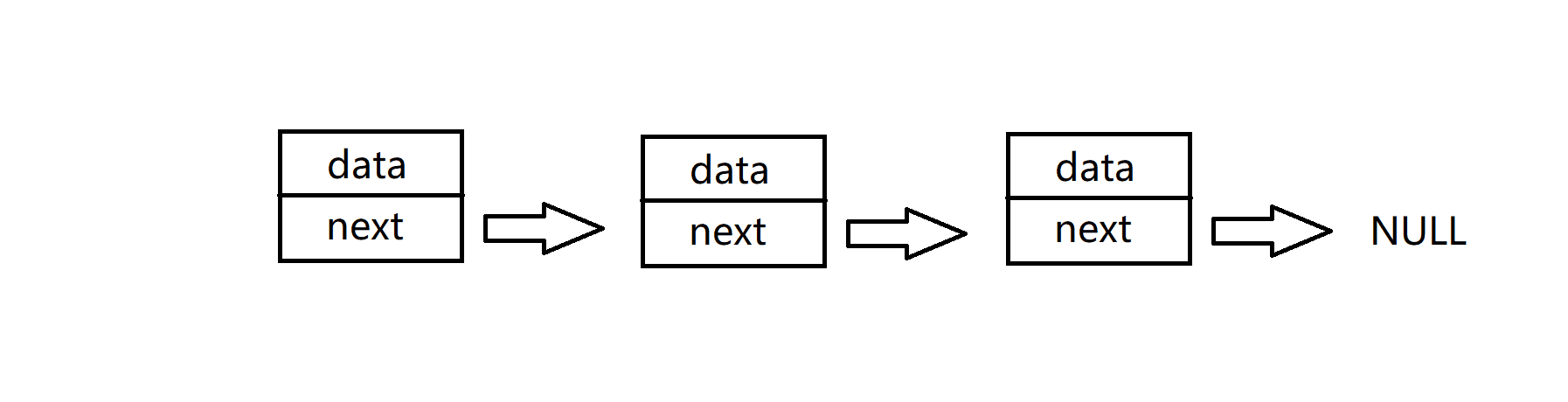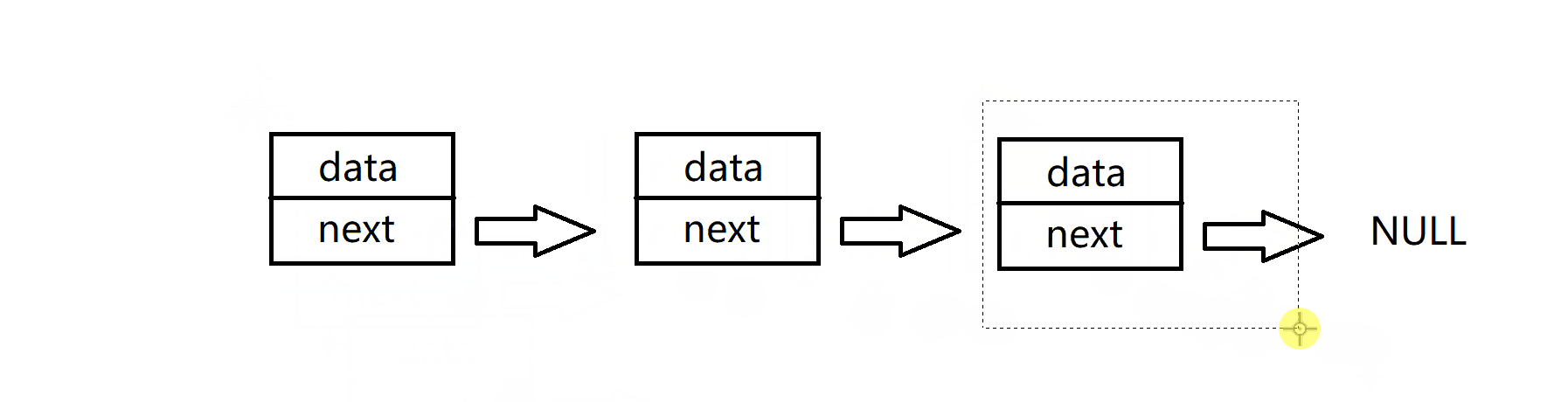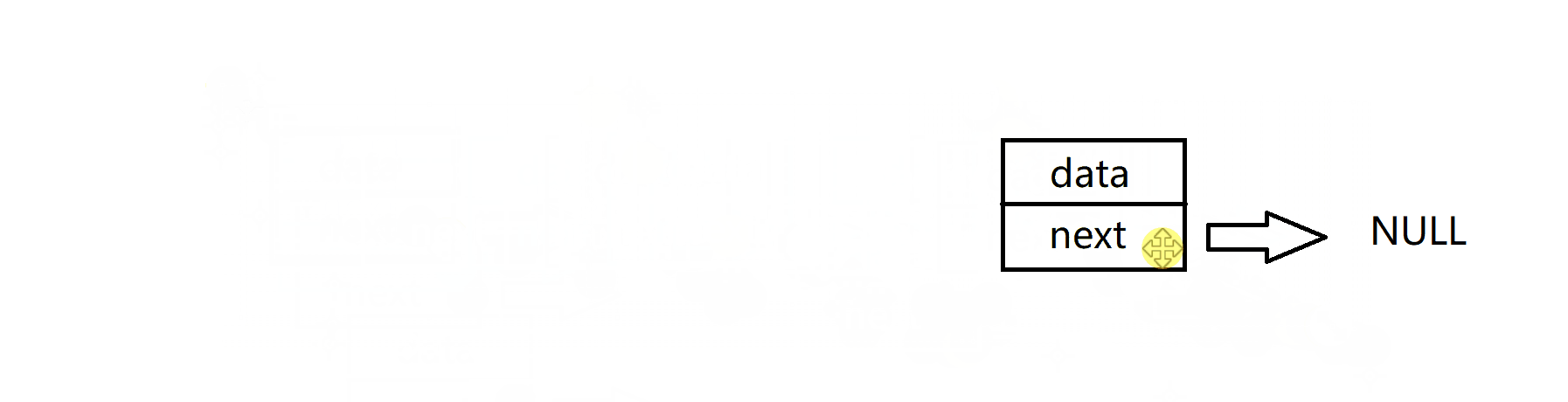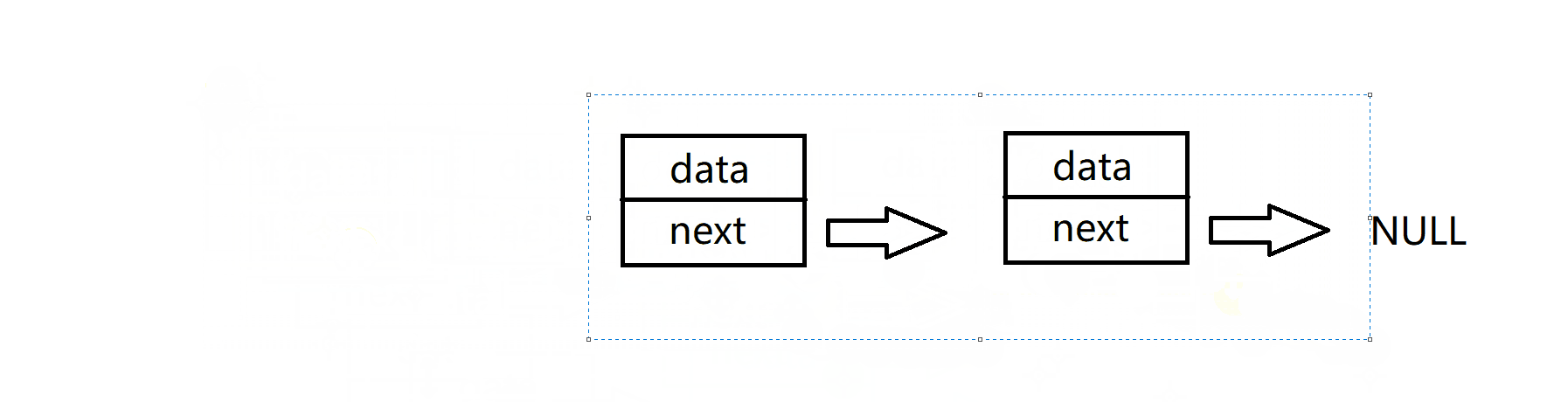
这里只需要完全使用链表的增删查改的操作函数即可，包括：顺序表的初始化，尾插，头删，判空，元素个数等

queue.h

#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>#define TYPE inttypedef struct QueueStructre
{int size;struct queueNode* front;struct queueNode* back;
}queue;typedef struct queueNode
{TYPE data;struct queueNode* next;
}Node;//初始化队列
void initqueue(queue* p);//初始化
void initqueue(queue* p);//初始化
void initqueue(queue* p);//队列只能尾插
void queuepush(queue* p, TYPE x);//队列只能头删
void queuepop(queue* p);//销毁
void destory(queue* p);//判断是否为空
bool QueueEmpty(queue* p);//计算元素个数
int QueueSize(queue* p); //找首元素
TYPE queuefront(queue* p);//找尾元素
TYPE queueback(queue* p);

queue.c

#include"queue.h"//初始化队列
void initqueue(queue* p)
{p->size = 0;p->front = NULL;p->back = NULL;
}//队列只能尾插
void queuepush(queue* p, TYPE x)
{Node* newcode = (Node*)malloc(sizeof(Node));if (newcode == NULL){perror("malloc fail");return;}newcode->data = x;newcode->next = NULL;if (QueueEmpty(p)){p->front = newcode;p->back = newcode;}else{p->back->next = newcode;p->back = newcode;}p->size++;
}//队列只能头删
void queuepop(queue* p)
{if (QueueEmpty(p)){return;}else{Node* n1 = p->front;Node* n2 = n1->next;p->front = n2;free(n1);p->size--;}
}//销毁
void destory(queue* p)
{Node* cur = p->front;while (cur){Node* next = cur->next;free(cur);cur = next;}p->front = NULL;p->back = NULL;p->size = 0;
}//判断是否为空
bool QueueEmpty(queue* p)
{return (p->size == 0);
}//计算元素个数
int QueueSize(queue* p)
{return p->size;
}//找首元素
TYPE queuefront(queue* p)
{return p->front->data;
}//找尾元素
TYPE queueback(queue* p)
{return p->back->data;
}

test.c

#include"queue.h"void test1()
{queue s;queue* p = &s;initqueue(p);queuepush(p,1);queuepush(p,2);queuepush(p,3);printf("%d\n", queuefront(p));printf("%d\n", queueback(p));printf("%d\n", QueueSize(p));queuepop(p);queuepush(p, 4);printf("%d\n", queuefront(p));printf("%d\n", queueback(p));destory(p);
}int main()
{test1();return 0;
}

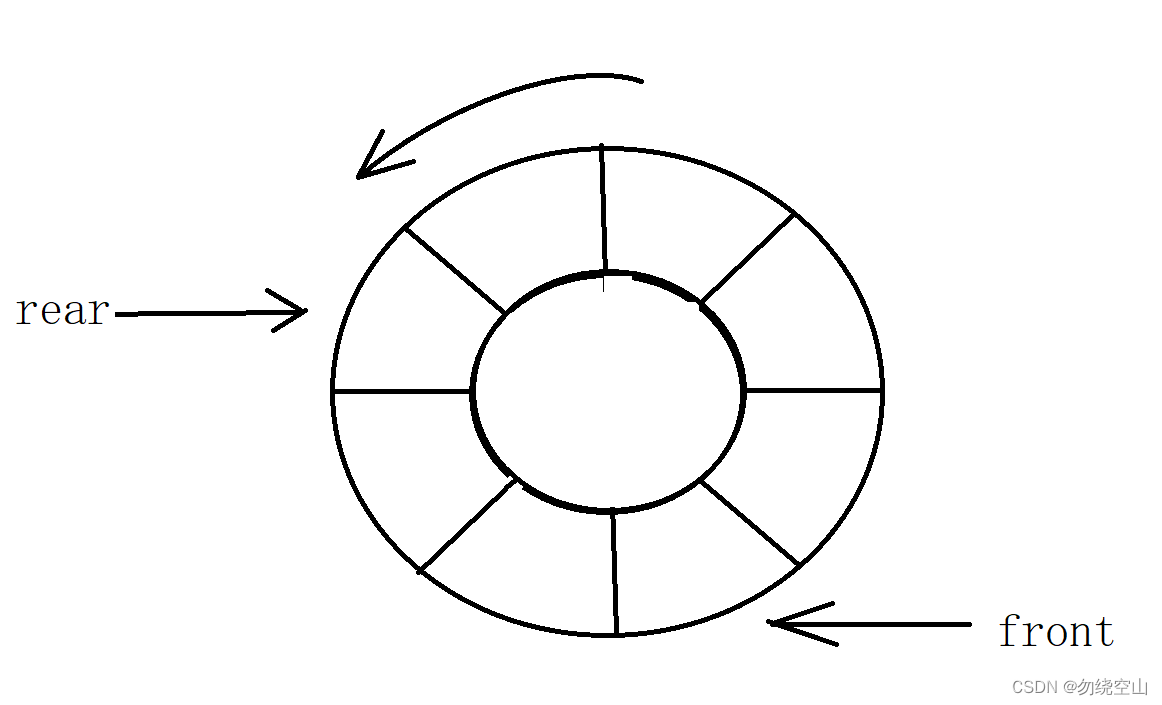
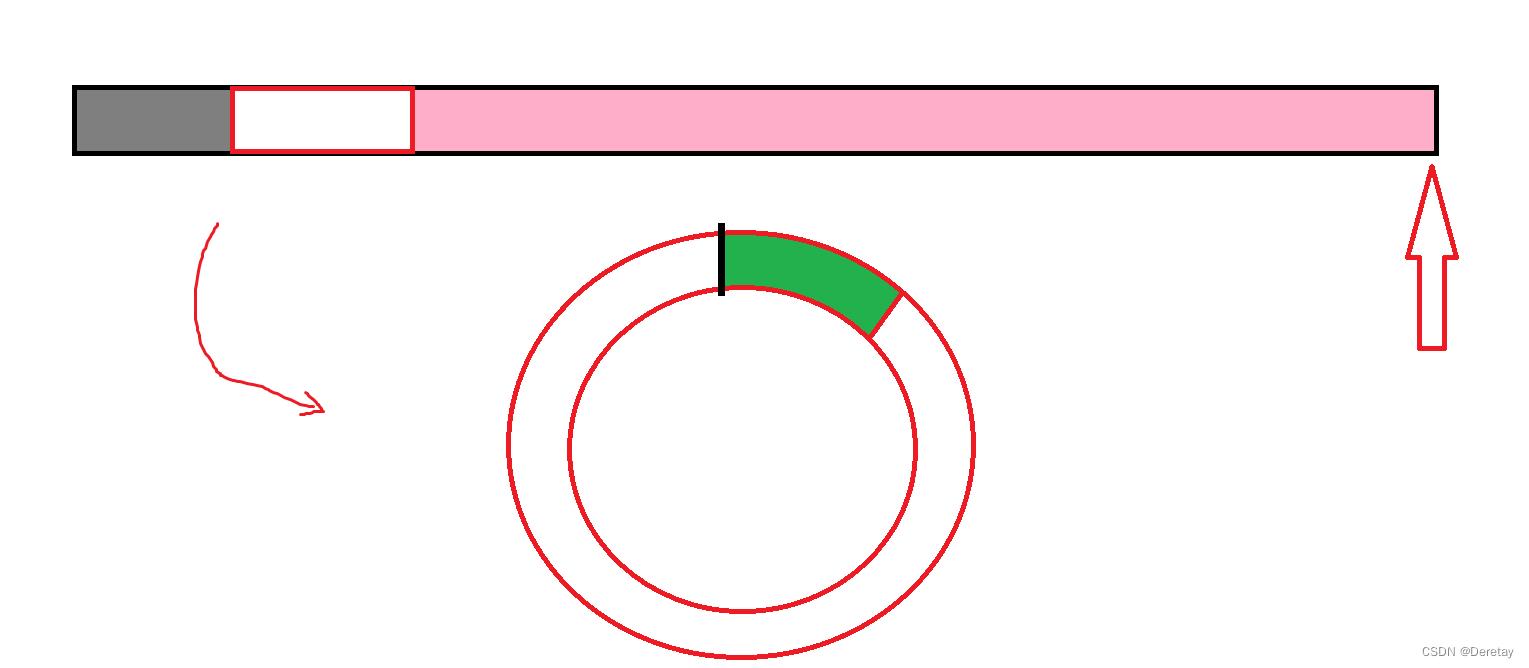
除此之外，还有一个特殊的循环队列，讲解如下：循环队列的实现_聪明的骑士的博客-CSDN博客