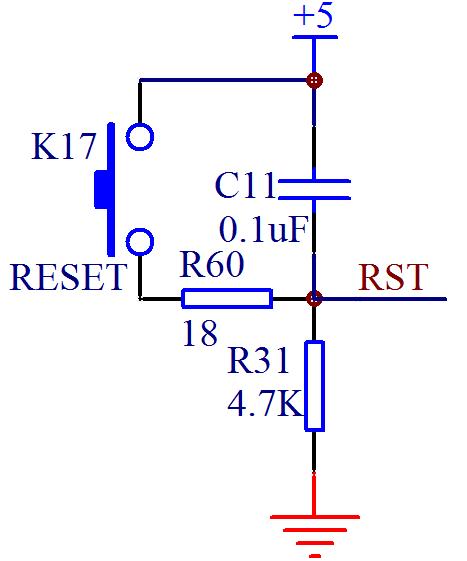
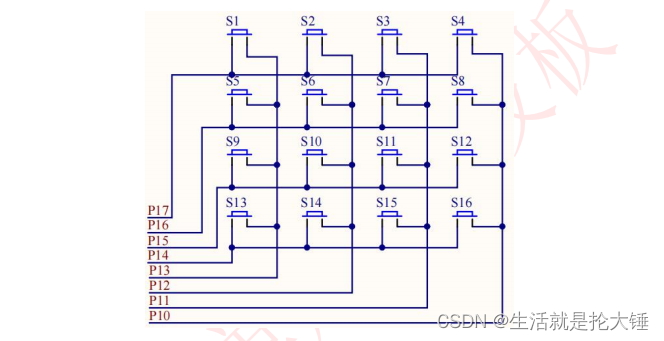
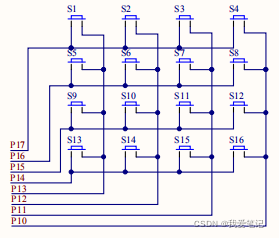
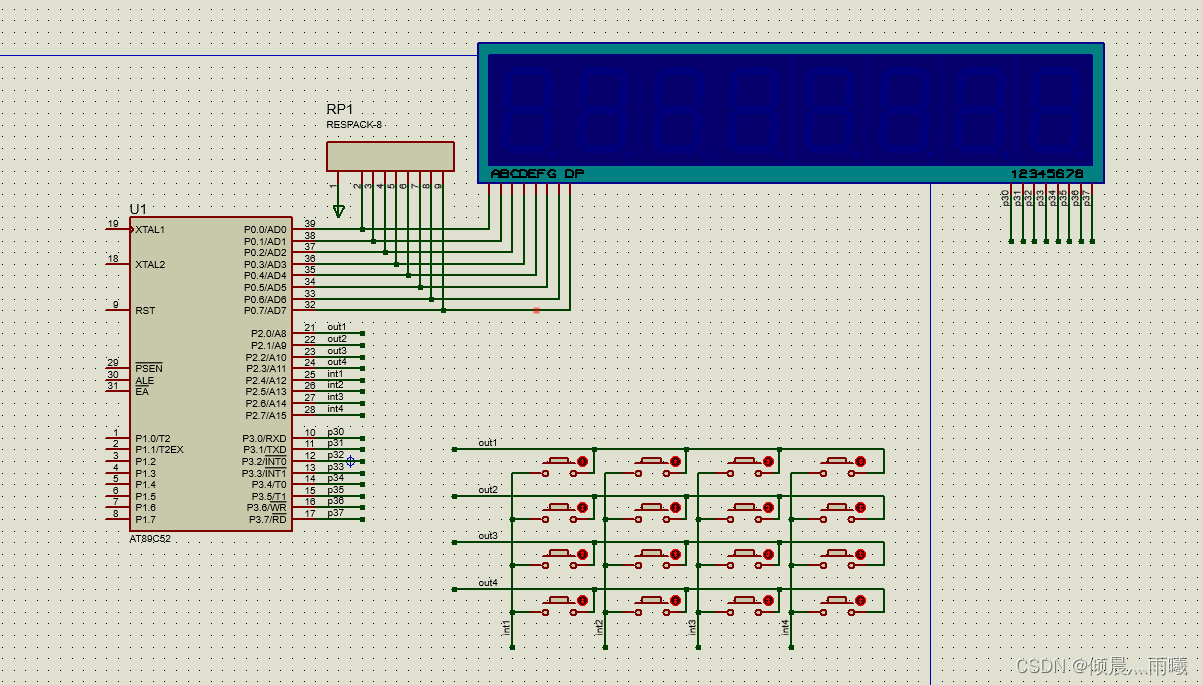
使用并行接口方式连接键盘，对独立式键盘而言，8根I/O口线可以接 **8** 个按键，而对矩阵式键盘而言，8根I/O口线最多可以接 **64** 个按键。

项目(工程)的时候，我们经常要用到比较多的按键，而且IO资源紧张，于是我们就想方设法地在别的模块中节省IO口，好不容易挤出一两个IO口，却发现仍然不够用，实在没办法了就添加一个IC来扫键。一个IC虽然价格不高，但对于大批量生产而且产品利润低的厂家来说，这是一笔不菲的开支!

那，我们能不能想到比较好的扫键方法：用最少的IO口，扫最多的键?可以吗?

举个例：给出5个IO口，能扫多少键?有人说是2*3=6个，如图一：

图一

对，大部分技术参考书都这么做，我们也经常这样做：用3个IO口作行扫描，2个IO作列检测(为方便描述，我们约定：设置某一IO口输出为“0”――称其为“扫某IO口”)。用行线输出扫键码，列线检测是否有按键的查询方法进行扫键。扫键流程：在行线依次输出011，101，110扫键值，行线每输出一个扫键值，列线检测一次。当列线检测到有按键时，结合输出的扫键值可以判断相应的按键。

但是，5个IO真的只能扫6个键吗?有人说可以扫9个，很聪明!利用行IO与地衍生3个键(要注意上拉电阻)，如图二：

图二

扫键流程：先检测3个行IO口，对K1’，K2’，K3’进行扫键，之后如上述2*3扫键流程。5个IO口能扫9个键，够厉害吧，足足比6个键多了1/2!

动动脑，还能不能再多扫几个?就几个?一个也行!好，再想一下，硬是被逼出来了!如图三：

不多不少，正好10个键!这种扫键方式比较少见吧!漂亮!扫键流程：设IO1输出为“0”，检测IO2…IO5，若判断有相应健按下，则可知有健;若无键，则继续扫键：设IO2输出为“0”，检测IO3，IO4，IO5，判断有无键按下，如此类推。这里应注意：当扫某一IO口(输出为“0”)时，不要去检测已经扫过的IO口。如：此时设置IO2输出为“0”，依次检测IO3,IO4,IO5，但不要去检测IO1，否则会出错(为什么，请思考)。

感觉怎么样?不错吧!让我们再看看图三，好有成就感!看着，看着……又看到了什么?快!见图四：

图四

真强!被您看出20个键!多了一个对称的三角形。可是，像这样的排列能正确扫20个键吗?回答是肯定的：不能!上下三角形相互对称，其对称扫出的键无法区别。有没有注意到分析图三时提到的注意点?(à“当扫某IO口时，不要去检测已经扫过的IO口，否则会出错”)

我们分析一下图四：当IO1输出“0”时，按下K11或K11’键都能被IO2检测到，但IO2检测却无法区别K11和K11’键!同理，不管扫哪个IO口，都有两个对称的键不能区分。

我们假想，如果能把对称键区分开来，我们就能正常地去判断按键。我们在思考：有没有单向导通性器件?有!见图五!

图五

很巧妙的思路!利用二极管的单向导通性，区别两个对称键。扫键思路：对逐个IO口扫键，其他四个IO口可以分别检测其所在的四个按键。这样，就不会有分析图三时提到的注意点。

够酷吧!等等，大家先别满足现状，我们再看一下图二，是不是有点启发?对，我们再分析一下“用5个IO口对地衍生的5个键”。看图六：

图六

25个键!5个IO口扫出25个键!先别激动，我们再分析一下它的可行性，分析通得过才能真正使用。假设扫键流程：先扫对地的5个键，再如图五扫键。先扫对地5个键，判断没有按键，接着对逐一对IO口进行扫键。但当对某一IO口扫键时，如果有对地的键按下，这时有可能会误判按键，因为对地键比其他键有更高的响应优先级。例如：扫IO1，IO1输出“0”，恰好此时K62按下，IO2检测到有按键，那就不能判断是K11还是K62。我们可以在程序上避免这种按键误判：若IO2检测到有按键，那下一步就去判断是否有对地键按下，如果没有，那就可以正确地判断是K11了。

我们小结扫键个数S：

S = (N-1)*N + N ――启用二极管

S = (N-1)*N /2 + N ――省掉二极管

很好很强大，真是学习了，以前都只会搞2*3的，涨姿势了