倍增

普及组的内容，思想很简单，但是考的可以挺难

倍增是啥东西

“ 倍增，顾名思义，就是每次增加一倍。 展开来说，就是每次根据已经得到的信息，将考虑的范围增加一倍， 从而加速操作。倍增思想有什么用呢？这是一种非常巧妙的思想，可以用来解决信息学竞赛中的很多问题。
考虑这样一个比较一般的模型，在一个有向图中，每个点最多只有 一条出边，每条边有一定的信息，走过一条路径时，就将路径上边的信息依次按一定的规则合并，并且合并的规则满足结合律。”

普通的线性倍增

问题：给定数组$a$和数字$T$,求最大的位置$k$,满足$sum(1->k)<=T$
那么我们就可以有2种做法：

1. 前缀和 + 二分
   这种代码应该挺简单
   如果不会前缀和的建议看一下前缀和和差分

#include <stdio.h>
#include <string.h>#include <iostream>const int MAXN = 5555555; 
int a[MAXN], pre[MAXN];
int n, k, t;inline void sum() {for (int i = 1; i <= n; ++i) {pre[i] = pre[i - 1] + a[i];}
}inline int bs(int l, int r) {int mid = l + r >> 1;if (pre[mid] > t) {if (pre[mid - 1] <= t) return mid  - 1;else return bs(l, mid);} else if (pre[mid] == t) return mid;else return bs(mid + 1, r);
}int main() {scanf("%d%d", &n, &t);for (int i = 1; i <= n; ++i) {scanf("%d", &a[i]);}sum();printf("%d\n", bs(1, n));return 0;
}

这里放一段代码(如果有bug请指出) -

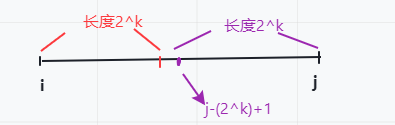
2.二分 + 倍增
画个图，大概是这样的：

二分不会的话，去看看这个 二分

树上倍增

树上倍增最经典的数LCA（最先公共祖先）了， 上次讲LCA模板搞出来了很多槽点

在图论和计算机科学中，最近公共祖先（英語：lowest common ancestor）是指在一个树或者有向无环图中同时拥有v和w作为后代的最深的节点。在这里，我们定义一个节点也是其自己的后代，因此如果v是w的后代，那么w就是v和w的最近公共祖先。
最近公共祖先是两个节点所有公共祖先中离根节点最远的，计算最近公共祖先和根节点的长度往往是有用的。比如为了计算树中两个节点v和w之间的距离，可以使用以下方法：分别计算由v到根节点和w到根节点的距离，两者之和减去最近公共祖先到根节点的距离的两倍即可得到v到w的距离。

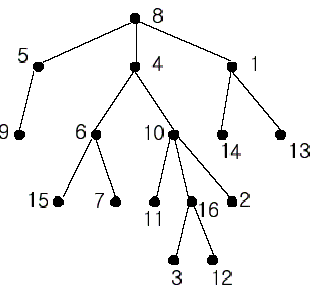
LCA模板：

inline void dfs(int index, int father) {  // index表示当前节点，father表示它的父亲节点fa[index][0] = father;//记录粑粑是哪一位depth[index] = depth[father] + 1;//深度自然就是他爸+1for (int i = 1; i <= lg[depth[index]]; ++i) fa[index][i] = fa[fa[index][i - 1]][i - 1];//第$2^i$个祖先是第$2^(i - 1)$个祖先的$2^(i - 1)$个祖先for (int i = head[index]; i; i = e[i].nxt)//遍历if (e[i].t != father) {//如果现在访问这个节点是自己的儿子(千万别把爸爸当做儿子了)dfs(e[i].t, index);//dfs}
}inline int LCA(int x, int y) {if (depth[x] < depth[y]) swap(x, y); // x喜欢在下面，看着y不顺眼就把y拉上去了(如果自己跳到y下面就会S)while (depth[x] > depth[y]) x = fa[x][lg[depth[x] - depth[y]] - 1]; //不过规定要一起去找LCA， 要同时跳到同一层()if (x == y) return x;//如果已经碰到一起了，LCA就是他们碰到的地方for (int k = lg[depth[x]] - 1; k >= 0; --k) //一起往上跳if (fa[x][k] != fa[y][k]) x = fa[x][k], y = fa[y][k];//得保证同时跳到的层析不是他们的LCAreturn fa[x][0]; //return theirs father(LCA)
}

RMQ & ST

RMQ和ST都有一个明显的特征：要预处理
那么什么时候要用到？
你看一下有m次或者q次询问的时候你就可以去想一下，很有可能这个就是RMQ & ST， 如果他的n数据范围很大、m(这个有可能是q、t等等)的数据范围也很大，并且$O(nlo{g}_{2}n)\le 10^8\times ms÷10^3$ 简单来说就是不会超时(如果$n\le 10000，m\le 10000$的话我觉得你可以试试看$O(m\times n)$)
关于代码吗， 这里写一小段 -> 因为没有注释，思路很明显 这是模板题的AC代码(请勿he题解)

#include <bits/stdc++.h>
using namespace std;
int f[100001][40], a, x, LC, n, m, p, len, l, r, lg[100001];signed main() {scanf("%d%d", &n, &m);for (int i = 1; i <= n; i++) {scanf("%d", &a);f[i][0] = a;lg[i] = lg[i >> 1] + 1;}LC = lg[n] / lg[2];for (int j = 1; j <= LC; j++) {for (int i = 1; i <= n - (1 << j) + 1; i++)  f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);}for (int i = 1; i <= m; i++) {scanf("%d%d", &l, &r);p = lg[r - l + 1] / lg[2];printf("%d\n", max(f[l][p], f[r - (1 << p) + 1][p]));}return 0;
}

倍增的思路还是挺经典的

end