一：定义

LCA指的是最近公共祖先。具体地，给定一棵有根数，若结点z既是结点x的祖先，也是结点y的祖先，则称z是x，y的公共祖先。在x，y的公共祖先中，深度最大的那个节点成为x，y的最近公共祖先，记为LCA(x,y)。

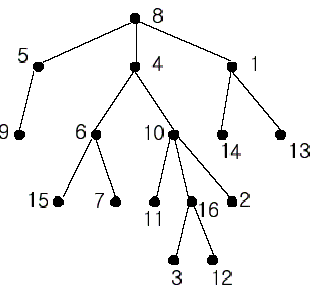
我们举个例子，如图4-4-1所示LCA（4,5)=2,LCA(5,6)=1,LCA(2,3)=1;

二：如何求LCA

我么考虑“暴力”要怎么实现找两点的LCA。

e.g. LCA(7,5）=2；

先DFS一遍找出每个点的DEP(深度)。然后先从深度大的7往上跳，跳到和5深度相同的点4，发现还是没有到同一个点，那么4、5继续往上跳，直到跳到2位置，发现点一样了，那么2就是它们的LCA了。

三：如何优化这个方法

我们考虑这个方法慢在哪里，当然是对于每个点，一次往上跳一步，导致了效率低，那么如何优化呢？只要一次能向上跳多步，效率自然就高了。

树上倍增法

树上倍增法是一个很重要的算法。设f[x,k]表示x的2^k辈祖先，即从x向根结点走
2^k步到达的结点，特别地，若该结点不存在，则令f[x,k]=0。f[x,0]就是x的父结点。 因为x向根结点走2^k <=> 向根走2^(k-1)步， 再走2^(k-1)步。
所以对于k∈[1,logn],有f[x][k]=f[f[x][k-1]][k-1]。

这类似于一个动态规划的过程，“阶段”就是结点的深度，因此，我们可以对树进行遍历，由此得到f[x.0]，再计算f数组所有值。
以上部分是预处理，时间复杂度为O(nlogn)。之后可以多次对不同的x，y计算LCA，每次询问的时间复杂度为O(logn)。

基于f数组计算LCA(x，y)分为以下几步：
①设dep[x]表示x的深度。不妨设dep[x]>=dep[y]。(否则，可交换x，y)。
②用二进制拆分思想，把x向上调整到与y同一深度。
具体来说，就是依次尝试从x向上走k=2^(logn)…...2^1，2^0步，若到达的结点比y深，则令x=f[x，k]。
③若此时x=y，说明已经找到了LCA，LCA就等于y。
④若此时x!=y，那么x，y继续往上跳，用二进制拆分思想，把x，y同时向上调整，并保持深度一致且二者不相会。
具体来说，就是依次尝试把x，y同时向上走k=2^(logn)…2^1，2^0步，若f[x，k]!=f[y，k].(即仍未相会)，则令x=f[x，k]，y=f[y，k]。
⑤此时x，y必定只差一步就相会了，它们的父结点f[x，0]就是LCA。

【代码实现】
预处理：

void Deal_first(int u,int father){Dep[u] = Dep[father] + 1;for(int i=0;i<=19;i++)f[u][i+1] = f[f[u][i]][i];for(int e=first[u];e;e=next[e]){int v=go[e];if(v == father)continue;f[v][0] = u;//v向上跳2^0 = 1就是uDeal_first(v,u);}
}

查询x,y的LCA：

int LCA(int x,int y){if(Dep[x]<Dep[y])swap(x,y);//让x深度较大
//我们用“暴力”的思想：先将x、y跳到一个深度，然后一起往上跳for(int i=20;i>=0;i--){//一定要倒着forif(Dep[f[x][i]]>=Dep[y])x=f[x][c][i];//先跳到同一层if(x==y) return x;}for(int i=20；i>=0；i--){//此时x，y已跳到同一层if(f[x][i]!=f[y][i])//如果f[x][i]和f[y][i]不同才跳{x=f[x][i];y=f[y][i];}}return f[x][0];//x,y是深度最浅且不同的点，即LCA的子结点
}

例题：

点的距离 LibreOJ - 10130

题目描述
给定一棵 n 个结点的树，Q个询问，每次询问点 x 到点 y 两点之间的距离。

输入格式
第一行一个正整数 n，表示这棵树有 n 个节点；
接下来 n-1 行，每行两个整数 x,y 表示 x,y 之间有一条连边；
然后一个整数 Q，表示有 Q 个询问；
接下来 Q 行每行两个整数 x,y 表示询问 x 到 y 的距离。

输出格式
输出 Q 行，每行表示每个询问的答案。

样例
Input
6
1 2
1 3
2 4
2 5
3 6
2
2 6
5 6
Output
3
4
数据范围与提示
对于全部数据，1≤n≤10^5,1≤x,y≤n。

分析：我们需要构建一棵树，然后距离就是x的深度+y的深度-LCA（x,y)的深度。
AC代码：

#include <bits/stdc++.h>
using namespace std;
const int ONE=100010;
int n,Q,x,y;
int nexx[ONE*2],first[ONE*2],go[ONE*2],tot;
int Dep[ONE];
int f[ONE][22];
void Add(int u,int v){nexx[++tot]=first[u];first[u]=tot;go[tot]=v;
}
void Deal_first(int u,int father){Dep[u]=Dep[father]+1;for(int i=0;i<=19;i++){f[u][i+1]=f[f[u][i]][i];}for(int e=first[u];e;e=nexx[e]){int v=go[e];if(v==father)continue;f[v][0]=u;Deal_first(v,u);	}
}
int LCA(int x,int y){if(Dep[x]<Dep[y])swap(x,y);for(int i=20;i>=0;i--){if(Dep[f[x][i]]>=Dep[y])x=f[x][i];if(x==y)return x;}for(int i=20;i>=0;i--){if(f[x][i]!=f[y][i]){x=f[x][i];y=f[y][i];}}return f[x][0];
}
int dist(int x,int y){return Dep[x]+Dep[y]-2*Dep[LCA(x,y)];
}
int main(){tot=0;scanf("%d",&n);for(int i=1;i<n;i++){scanf("%d%d",&x,&y);Add(x,y);Add(y,x);}Deal_first(1,0);scanf("%d",&Q);while(Q--){scanf("%d%d",&x,&y);printf("%d\n",dist(x,y));}return 0;
}

详细请看一本通