朴素算法求LCA,即暴力求解,当树近乎为一条链时,找祖先时一级一级向上跳,时间复杂度接近O(n),所以可以考虑一次跳尽可能大的距离,即倍增算法;一次跳2^i(i=0,1,2....)级。
倍增法 一个节点的四级祖先就是这个节点的二级祖先的二级祖先;
设fa[j][i]为j节点的2^i级祖先;则fa[j][i]=fa[fa[j][i-1]][i-1];
算法思想:求两节点的lca,先将深度深的结点用倍增法向上跳,直到两节点处于同一深度,此时有可能重合,则两点中任意一个结点即为lca;若没重合,则两节点同时用倍增法上跳,直到两节点的父亲节点重合,则两点中任意节点的父亲节点即为lca。
模板题 POJ-1330 求两节点的lca
数据结构中的树,在计算机科学中是非常重要的,例如我们来看看下面这棵树:
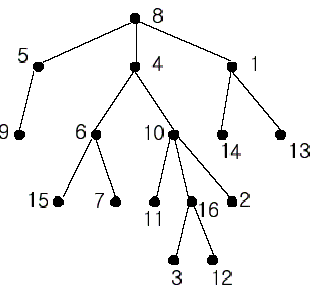
在图中我们对每个节点都有编号了。 8号节点是这棵树的根。我们定义,一个子节点向它的根节点的路径上,任意一个节点都称为它的祖先。例如, 4号节点是16号节点的祖先。而10号节点同样也是16号的祖先。事实上,16号的祖先有8,4,10,16共四个。另外8, 4, 6,7都是7号节点的祖先,所以7号和16号的公共祖先是4和8号,而在这两个里面,4号是距离7和16最近的一个,所以我们称7号和16号的最近公共祖先是4号。
再例如,2和3的最近公共祖先是10,再例如6和13的是8。
现在你需要编写一个程序,在一棵树中找出指定两个节点的最近公共祖先
Input
第一行输入T表示有T组数据。每组第一行是N表示这棵树有多少个节点,其中 2<=N<=10,000。 节点用正整数1, 2,..., N表示。 接下来的 N -1 行表示这棵树的边,每行两个数,都是节点编号,前一个是后一个的父节点。最后一行是要查询的两个节点,计算出这两个节点的最近公共祖先
Output
对于每组测试输出一行,输出它们的最近公共祖先的编号。
Sample Input
2 16 1 14 8 5 10 16 5 9 4 6 8 4 4 10 1 13 6 15 10 11 6 7 10 2 16 3 8 1 16 12 16 7 5 2 3 3 4 3 1 1 5 3 5
Sample Output
4 3
#include<iostream>
#include<algorithm>
#include<vector>
#include<cstring>
using namespace std;
const int N=1e4+5;
int n;
vector<int>G[N];
int f[N][30];//祖先信息,f[j][i],节点j的2^i级祖先,f[j][0]即为节点j的父节点
int dep[N];//节点深度信息
void dfs(int u,int f,int d)
{dep[u]=d;for(int i=0;i<G[u].size();i++){if(G[u][i]!=f)dfs(G[u][i],u,d+1);}
}void init(int n)
{int x=1;while(f[x][0]!=-1)x=f[x][0];//找到根节点dfs(x,-1,0);for(int i=1;i<=20;i++){for(int j=1;j<=n;j++){f[j][i]=f[f[j][i-1]][i-1];//预处理}}
}
int lca(int x,int y)
{if(dep[x]<dep[y])swap(x,y);
// for(int i=20;i>=0;i--)
// {
// if(dep[f[x][i]]>=dep[y]) //用此方法一直wa
// x=f[x][i];
// }for(int i=0;i<=20;i++)if((dep[x]-dep[y])>>i&1) //AC x=f[x][i];if(x==y)return x;for(int i=20;i>=0;i--){if(f[x][i]!=f[y][i])x=f[x][i],y=f[y][i];}return f[x][0];
}
int main()
{int t;cin>>t;while(t--){cin>>n;memset(f,-1,sizeof(f));memset(dep,0,sizeof(dep));for(int i=0;i<=n;i++)G[i].clear();for(int i=1;i<n;i++){int a,b;cin>>a>>b;f[b][0]=a;G[a].push_back(b);G[b].push_back(a);}init(n); int x,y;cin>>x>>y;cout<<lca(x,y)<<endl;}return 0;} POJ-1986
John是一个农场主,他有许多农场,每个农场里都会养一些牛,并且他的农场有一个特点,就是每两个农场之间,至多存在一条路线。他有时需要将某个农场的牛带到另一个农场去,但是,他的牛都懒散惯了,所以John想为他的牛找到一条最短的路线。先给出John的农场地图,请你为他计算某两个农场间的最短距离。
输入格式
第一行给出两个整数 n,m(n,m\le 40000)n,m(n,m≤40000),表示农场数和道路数。
接下来有 mm 行,每行给出三个整数 a,b,ca,b,c 和一个字符 xx,表示农场 aa 到农场 bb 的有一条直接相连的长度为 cc 的道路,字符 xx 只会是N,S,W,EN,S,W,E,表示north, south, west, east,指从农场a到农场b的道路的方向。注意:所有道路都是双向道路。
接下来一行给出一个整数 k(1\le k\le10000)k(1≤k≤10000),表示询问次数。
接下来有 kk 行,每行给出两个整数 a,ba,b,表示询问农场 aa 到农场 bb 的最短距离。
本题为POJ的题目,请使用G++提交,并且头文件中不能包含unordered_map。
输出格式
对于每个询问,输出农场 aa 到农场 bb 的最短距离。
每行输出末尾不能有多余空格。
输入样例
7 6 1 6 13 E 6 3 9 E 3 5 7 S 4 1 3 N 2 4 20 W 4 7 2 S 3 1 6 1 4 2 6
输出样例
13 3 36
心得:
输入的N,E,S,W貌似没啥用
这题的不像上面那道题(在输入边时,告诉了两节点中谁是谁的父亲节点),未告诉父亲节点的信息,不妨都把节点1当作根节点,然后dfs中保存节点的父亲节点信息就行了。
这题是lca求树上最短路的典型例题,(树:有n个节点,n-1条边),例如求x,y的最短路,x,y之间的最短路=x到根节点的距离+y到根节点的距离 - 2倍的lca(x,y)到根节点的距离。
#include<iostream>
#include<vector>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=4e4+5;
struct edge{int to,cost;
};
vector<edge>G[N];
int dep[N],fa[N][30],dis[N];
int t,n,m;
void dfs(int u,int f,int d)
{dep[u]=d;for(int i=0;i<G[u].size();i++){edge e=G[u][i];if(e.to!=f){ //不是父节点,再进行下面操作 dis[e.to]=dis[u]+e.cost;//保存节点到根节点1的距离fa[e.to][0]=u;//保存节点的父亲节点dfs(e.to,u,d+1);}}
}
void init()
{dis[1]=0;
// fa[1][0]=1;dfs(1,-1,0);for(int i=1;i<=20;i++){for(int j=1;j<=n;j++){fa[j][i]=fa[fa[j][i-1]][i-1];}}
}
int lca(int x,int y)
{if(dep[x]<dep[y])swap(x,y);for(int i=0;i<=20;i++){if((dep[x]-dep[y])>>i&1)x=fa[x][i];}
// for(int i=20;i>=0;i--)
// {
// if(dep[fa[x][i]]>=dep[y])//此方法也能AC
// x=fa[x][i];
// } if(x==y)return x;for(int i=20;i>=0;i--){if(fa[x][i]!=fa[y][i])x=fa[x][i],y=fa[y][i];}return fa[x][0];
}int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=m;i++){int a,b,c;char cc;scanf("%d%d%d",&a,&b,&c);cin>>cc;edge e;e.cost=c;e.to=b;G[a].push_back(e);e.to=a;G[b].push_back(e);}init();int q;cin>>q;for(int i=1;i<=q;i++){int x,y;scanf("%d%d",&x,&y);// int l=lca(x,y);cout<<dis[x]+dis[y]-2*dis[lca(x,y)]<<endl;}return 0;} 





![[2022.8.15]v4l2-ctl基本使用方法](https://img-blog.csdnimg.cn/503d7de97a994bee9c7737ea53e1838b.png)