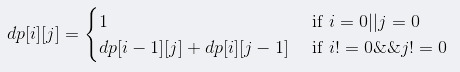---

跳跃游戏 VI (滑动窗口+动态规划)

解题思路：

本题其实很好找到状态转移方程：

$dp[i]$ : 跳到i位置的最大和 $dp[i]=max(dp[i-1],dp[i-2],.....dp[i-k])+nums[i]$
但是，很显然，每次遍历 $dp[i-1],dp[i-2],.....dp[i-k]$ 的复杂度是 $O(N)=10^5$ , 再加上遍历 $i=0$ 到$n-1$ 复杂度也是 $O(N)=10^5$ ，超时，优化办法是用滑动窗口，维护 $max(dp[i-1],dp[i-2],.....dp[i-k])$

class Solution {
public://动态规划+滑动窗口int DP(vector<int>& nums, int k){int n=nums.size();//dp[i]: 到达i位置最大得分vector<int>dp(n,0);dp[0]=nums[0];int wl=0,wr=0;//窗口的左右边界[wl,wr]list<int>slideWindow;slideWindow.push_back(0);for(int i=1;i<n;++i){//维持一个大小为k的窗口[i-k,i-1]dp[i]=dp[slideWindow.front()]+nums[i];if(wr-wl+1<k){//窗口右边界右移while(!slideWindow.empty()&&dp[i]>dp[slideWindow.back()]){slideWindow.pop_back();}slideWindow.push_back(i);wr++;}else{//窗口左右边界都要右移while(!slideWindow.empty()&&dp[i]>dp[slideWindow.back()]){slideWindow.pop_back();}slideWindow.push_back(i);wr++;wl++;if(slideWindow.front()<wl){//过期了slideWindow.pop_front();}}}// for(int i=0;i<n;++i){//     cout<<dp[i]<<" ";// }return dp[n-1];}int maxResult(vector<int>& nums, int k) {return DP(nums,k);}
};

---

丑数

class Solution {
public:int nthUglyNumber(int n) {int index2=0,index3=0,index5=0;int min=1;vector<int>dp(n,1);for(int i=1;i<n;++i){min=std::min({dp[index2]*2,dp[index3]*3,dp[index5]*5});dp[i]=min;if(min==dp[index2]*2){index2++;}if(min==dp[index3]*3){index3++;}if(min==dp[index5]*5){index5++;}}return min;}
};

---

统计字典序元音字符串的数目

class Solution {
public:int DP(int n){//dp[0]: 以a开头的字符串数量,dp[1]:以e开头的字符串数量,......vector<int>dp(5,1);for(int i=2;i<=n;++i){//长度为i的字符串数量//以a,e,i,o,u开头的字符串可以在前面加a//以e,i,o,u开头的字符串可以在前面加e//..........for(int j=0;j<5;++j){//更新长度为i的字符串中分别以a,e,i,o,u开头的字符串数量for(int k=j+1;k<5;++k){dp[j]+=dp[k];}}}return dp[0]+dp[1]+dp[2]+dp[3]+dp[4];}int countVowelStrings(int n) {return DP(n);}
};

---

最长重复子串

class Solution {
public:int DP(string& s){int n=s.length();//dp[i][j]: 以s[i],s[j]结尾的两个相同的字串的长度int res=0;auto dp=vector<vector<int>>(n,vector<int>(n,0));for(int j=1;j<n;++j){dp[0][j]=s[j]==s[0]?1:0;}for(int i=1;i<n;++i){for(int j=i+1;j<n;++j){if(s[i]==s[j]){dp[i][j]=dp[i-1][j-1]+1;}res=res>dp[i][j]?res:dp[i][j];}}return res;}int longestRepeatingSubstring(string s) {return DP(s);}
};

---

分隔数组以得到最大和

class Solution {
public:int DP(vector<int>& arr, int k){int n=arr.size();vector<int>dp(n,0);//dp[i]: 0~i上将数组分割，获得的最大元素和int max=0;for(int i=0;i<k;++i){max=std::max(max,arr[i]);dp[i]=(i+1)*max;}for(int i=k;i<n;++i){dp[i]=dp[i-1]+arr[i];//nums[i]单独一个组for(int j=i-1;j>=i-k+1;--j){//arr[j...i]分成一个组max=0;for(int r=j;r<=i;++r){max=std::max(max,arr[r]);}dp[i]=std::max(dp[i],dp[j-1]+(i-j+1)*max);}}// for(int i=0;i<n;++i){//     cout<<dp[i]<<" ";// }return dp[n-1];}int maxSumAfterPartitioning(vector<int>& arr, int k) {return DP(arr,k);}
};

---

最低票价

class Solution {
public:int DP(vector<int>& days, vector<int>& costs){int n=days.size();//dp[i]: 完成日期i的旅行的最低消费vector<int>dp(366);dp[days[0]]=min({costs[0],costs[1],costs[2]});for(int i=1;i<n;++i){int date=days[i];for(int j=days[i-1]+1;j<date;++j)dp[j]=dp[j-1];dp[date]=dp[date-1]+min({costs[0],costs[1],costs[2]});if(date-7>=1){dp[date]=min(dp[date],dp[date-7]+costs[1]);}else{dp[date]=min(dp[date],dp[0]+costs[1]);}if(date-30>=1){dp[date]=min(dp[date],dp[date-30]+costs[2]);}else{dp[date]=min(dp[date],dp[0]+costs[2]);}}// for(int i=0;i<30;++i){//     cout<<dp[i]<<" ";// }return dp[days[n-1]];}int mincostTickets(vector<int>& days, vector<int>& costs) {return DP(days,costs);}
};

---

回文子串

解题思路:

$dp[i][j]$ : 子串 $s[i..j]$ 是否是回文，如果是，$cnt$ ++ , 这样就能统计出所有的回文子串

class Solution {
public:int DP(string& s){int n=s.length();int cnt=0;//dp[i][j]: 字串s[i..j]是否是回文auto dp=vector<vector<bool>>(n,vector<bool>(n,false));for(int i=0;i<n;++i){dp[i][i]=true;++cnt;}for(int col=1;col<n;++col){for(int i=0,j=col;j<n;++i,++j){dp[i][j]=(s[i]==s[j])&&(i+1>j-1?true:dp[i+1][j-1]);if(dp[i][j])++cnt;}}// for(int i=0;i<n;++i){//     for(int j=0;j<n;++j){//         cout<<dp[i][j]<<" ";//     }cout<<endl;// }return cnt;}int countSubstrings(string s) {return DP(s);}
};

---

最长重复子数组

class Solution {
public:int DP(vector<int>& nums1, vector<int>& nums2){int m=nums1.size();int n=nums2.size();//dp[i][j]: nums1[0...i] 与 nums2[0....j] 且nums1[i],nums2[j]结尾的最长公共子数组长度auto dp=vector<vector<int>>(m,vector<int>(n,0));int res=0;for(int col=0;col<n;++col){if(nums2[col]==nums1[0]){dp[0][col]=1;}res=res>dp[0][col]?res:dp[0][col];}for(int row=1;row<m;++row){if(nums1[row]==nums2[0]){dp[row][0]=1;}res=res>dp[row][0]?res:dp[row][0];}for(int i=1;i<m;++i){for(int j=1;j<n;++j){if(nums1[i]==nums2[j]){dp[i][j]=1+dp[i-1][j-1];}res=res>dp[i][j]?res:dp[i][j];}}return res;}int findLength(vector<int>& nums1, vector<int>& nums2) {return DP(nums1,nums2);}
};

---

最长回文子序列

解题思路：

状态转移方程：

如果 $s[i]==s[j]:dp[i][j]=2+dp[i+1][j-1]$

否则 $dp[i][j]=max(dp[i+1][j],dp[i][j-1])$

class Solution {
public:int DP(string& s){//dp[i][j]: [i,j]范围内最长回文子序列长度int n=s.length();auto dp=vector<vector<int>>(n,vector<int>(n,0));for(int i=0;i<n;++i){dp[i][i]=1;}for(int c=1;c<n;++c){for(int i=0,j=c;i<n-c;++i,++j){if(s[i]==s[j]){dp[i][j]=dp[i+1][j-1]+2;}else{dp[i][j]=dp[i][j-1]>dp[i+1][j]?dp[i][j-1]:dp[i+1][j];}}}return dp[0][n-1];}int longestPalindromeSubseq(string s) {return DP(s);}
};

---

摆动序列

class Solution {
public:int DP(vector<int>& nums){int n=nums.size();if(n==1)return 1;vector<int>dp(n,1);//dp[i]: 以nums[i]结尾的最长子序列长度//sign[i] :以nums[i]结尾的最长子序列正负vector<int>sign(n,0);int res=1;for(int i=1;i<n;++i){for(int j=i-1;j>=0;--j){if(dp[j]==1){if(dp[i]<2){if(nums[i]!=nums[j]){dp[i]=2;sign[i]=nums[i]-nums[j]<0?-1:1;} }}else{if(nums[i]!=nums[j]&&sign[j]*(nums[i]-nums[j])<0){if(dp[i]<dp[j]+1){dp[i]=dp[j]+1;sign[i]=nums[i]-nums[j]<0?-1:1;}}}}res=res>dp[i]?res:dp[i];}return res;}int wiggleMaxLength(vector<int>& nums) {return DP(nums);}
};

---

旋转函数

class Solution {
public:int DP(vector<int>& nums){int n=nums.size();vector<long>dp(n,0);int sum=0;for(int i=0;i<n;++i){sum+=nums[i];dp[0]+=i*nums[i];}int res=dp[0];//dp[i]: 第i次旋转//0 :4 3 2 6//1 :6 4 3 2//2 :2 6 4 3//3 :3 2 6 4//4 :4 3 2 6//5 :6 4 3 2for(int i=1;i<n;++i){//每旋转一次,相当于加上数组和，再减去n*(当前数组最后一个元素)//当前数组最后一个元素在原数组中的下标是: (n-i%4)dp[i]=dp[i-1]+sum-n*nums[n-i%n];res=dp[i]>res?dp[i]:res;}return res;}int maxRotateFunction(vector<int>& nums) {return DP(nums);}
};

---

统计各位数字都不同的数字个数 (动规+排列组合)

class Solution {
public:int DP(int n){if(n==0)return 1;vector<int>dp(n+1,0);//dp[0]: [0~10^0)有多少个x//dp[i]:[10^(i-1),10^i)有多少个xdp[0]=1;//0int w[]={9,9,8,7,6,5,4,3,2,1};for(int i=1;i<=n;++i){//根据排列组合 dp[i]=9*9*8...+dp[i-1];int mul=1;//i位数for(int j=0;j<i;++j){mul*=w[j];}dp[i]=dp[i-1]+mul;}return dp[n];}int countNumbersWithUniqueDigits(int n) {return DP(n);}
};

---

最大整除子集

class Solution {
public:vector<int>res;void DP(vector<int>& nums){//dp[i]: 以nums[i]结尾的最大的整除子集,初始化为1//pre[i]: 以nums[i]结尾的最大的整除子集的前一个下标位置,初始化为-1//排序数组sort(nums.begin(),nums.end());int n=nums.size();vector<int>dp(n,1);vector<int>pre(n,-1);for(int i=1;i<n;++i){//求dp[i]for(int j=i-1;j>=0;--j){//当前的整除子集是有序的，只要nums[j]可以整除nums[i]，//且长度大于当前dp[i]，就更新dp[i]if(nums[i]%nums[j]==0&&dp[j]+1>dp[i]){dp[i]=dp[j]+1;pre[i]=j;}}}int end=0;//end是最大整除子集的结尾下标int maxSize=1;for(int i=0;i<n;++i){if(maxSize<dp[i]){maxSize=dp[i];end=i;}}while(end!=-1){res.push_back(nums[end]);end=pre[end];}reverse(res.begin(),res.end());}vector<int> largestDivisibleSubset(vector<int>& nums) {DP(nums);return res;}
};

---

猜数字大小 II

class Solution {
public:int DP(int n){//dp[i][j]: [i,j]上猜数字,确保获胜的最小现金数auto dp=vector<vector<int>>(n+1,vector<int>(n+1,INT_MAX));for(int i=1;i<=n;++i){dp[i][i]=0;}for(int c=2;c<=n;++c){for(int i=1,j=c;i<=n-c+1;++i,++j){// cout<<i<<" "<<j<<endl;//遍历我猜的数[i,j]for(int k=i+1;k<j;++k){ //k=i,k=j要单独算//正确的数<k k+dp[i][k-1]//正确的数>k k+dp[k+1][j]//为了确保肯定获胜：应该取两种情况的最大值dp[i][j]=min(dp[i][j],max(dp[i][k-1],dp[k+1][j])+k); }dp[i][j]=min(dp[i][j],dp[i+1][j]+i);  dp[i][j]=min(dp[i][j],dp[i][j-1]+j);}}return dp[1][n];}int getMoneyAmount(int n) {return DP(n);}
};

---

超级丑数

class Solution {
public:int nthSuperUglyNumber(int n, vector<int>& primes) {if(n==1)return 1;int m=primes.size();int index[m];for(int i=0;i<m;++i){index[i]=1; }int dp[n+1];dp[1]=1;for(int i=2;i<=n;++i){int minVal=INT_MAX;for(int j=0;j<m;++j){if(index[j]<=n&&dp[i-1]<dp[index[j]]*primes[j]){minVal=std::min(minVal,dp[index[j]]*primes[j]);}}dp[i]=minVal;for(int j=0;j<m;++j){if(index[j]<=n&&minVal==dp[index[j]]*primes[j]){++index[j];}}}return dp[n];}
};

---

预测赢家

解题思路：

定义一个二维数组，先明确是用来干什么的，dp[i][j] 表示两个玩家在数组 i 到 j 区间内游戏能赢对方的差值（i <= j）。

假如玩家1先取左端 nums[i]，那么玩家2能赢对方的差值是dp[i+1][j] ，如果玩家1先取取右端 nums[j]，玩家2能赢对方的差值就是dp[i][j-1]，

那么 不难理解如下公式：

$dp[i][j]=max((nums[i]-dp[i+1][j]),(nums[j]-dp[i][j-1]));$

确定了状态转移公式之后，就要想想如何遍历。

一些同学确定的方程，却不知道该如何遍历这个遍历推算出方程的结果，我们来看一下。

首先要给dp[i][j]进行初始化，首先当i == j的时候，nums[i]就是dp[i][j]的值。

class Solution {
public:int DP(vector<int>& nums){//dp[i][j]:区间[i,j]上,能赢对方的最大差值(可能为负值)int n=nums.size();if(n==1)return nums[0];auto dp=vector<vector<int>>(n,vector<int>(n,0));for(int i=0;i<n;++i){dp[i][i]=nums[i];}for(int c=1;c<n;++c){//每次开始的列是cfor(int r=0;r<n-c;++r){dp[r][c+r]=max(nums[c+r]-dp[r][c+r-1],nums[r]-dp[r+1][c+r]);}}return dp[0][n-1];}bool PredictTheWinner(vector<int>& nums) {return DP(nums)>=0;}
};

---

栅栏涂色

class Solution {
public:int DP(int n,int k){//dp[i][0]:i个栅栏柱,且第i个栅栏柱与第i-1个颜色相同的方案数//dp[i][1]:i个栅栏柱,且第i个栅栏柱与第i-1个颜色不相同的方案数if(n==1)return k;if(n==2)return k*k;vector<vector<int> >dp(n+1,vector<int>(2,0));dp[1][0]=0;dp[1][1]=k;for(int i=2;i<=n;++i){dp[i][0]=dp[i-1][1];dp[i][1]=(dp[i-1][0]+dp[i-1][1])*(k-1);}return dp[n][0]+dp[n][1];}int numWays(int n, int k) {return DP(n,k);}
};

---

丑数 II

class Solution {
public://本题关键思路：每个丑数都是由更小的丑数要么*2,要么*3,要么*5得到的int DP(int n){//dp[i]: 第i个丑数vector<long long>dp(n+1,INT_MAX);if(n==1)return 1;dp[1]=1;int index2=1;//使得2*x>第i-1个丑数的int index3=1;int index5=1;for(int i=2;i<=n;++i){dp[i]=min(dp[index2]*2,min(dp[index3]*3,dp[index5]*5));if(dp[i]==dp[index2]*2)index2++;if(dp[i]==dp[index3]*3)index3++;if(dp[i]==dp[index5]*5)index5++;}return dp[n];}int nthUglyNumber(int n) {return DP(n);}
};

---

粉刷房子

class Solution {
public:int DP(vector<vector<int>>& costs){int n=costs.size();if(n==1)return min(costs[0][0],min(costs[0][1],costs[0][2]));//dp[i][j]:0~i号房子被粉刷且用j颜色粉刷i房子的最小花费auto dp=vector<vector<int> >(n,vector<int>(3,0));dp[0][0]=costs[0][0];dp[0][1]=costs[0][1];dp[0][2]=costs[0][2];for(int i=1;i<n;++i){dp[i][0]=costs[i][0]+min(dp[i-1][1],dp[i-1][2]);dp[i][1]=costs[i][1]+min(dp[i-1][0],dp[i-1][2]);dp[i][2]=costs[i][2]+min(dp[i-1][1],dp[i-1][0]);}return min(dp[n-1][0],min(dp[n-1][1],dp[n-1][2]));}int minCost(vector<vector<int>>& costs) {return DP(costs);}
};

---