一.动态规划三要素

1.最优子结构

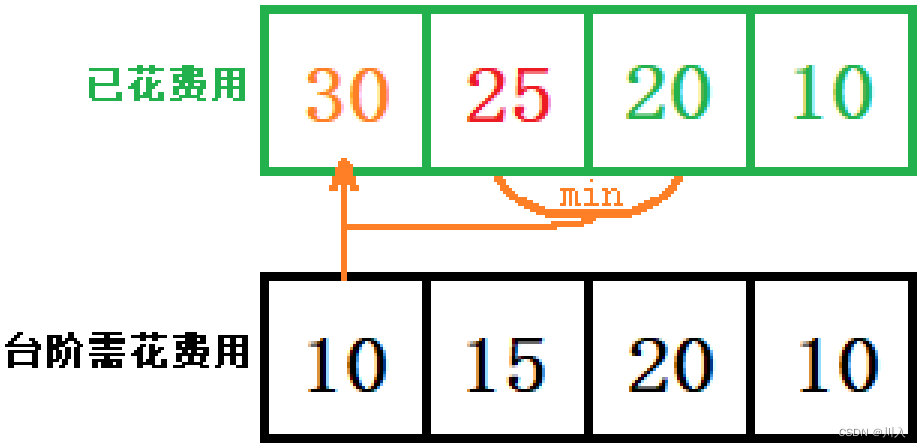
2.状态转移方程（核心）（一般用打表找出规律）

3.边界值

二.背包问题

（一.题目）

1.1题目描述

现在有一个背包但容量有限，最多只能装m千克宝石!有n个宝石，每个宝石都有自己的重量m和价值c。求可以装的宝石的最大价值。

1.2输入输出描述

输入：两个整数m和n，表示背包最大容量和宝石数量

接下来的n行分别表示每个宝石的重量和价值

输出：可以装的宝石的最大价值

1.3样例

输入：

8 3
2 3
5 4
5 5

输出：

8

（二.思路）

打表找规律

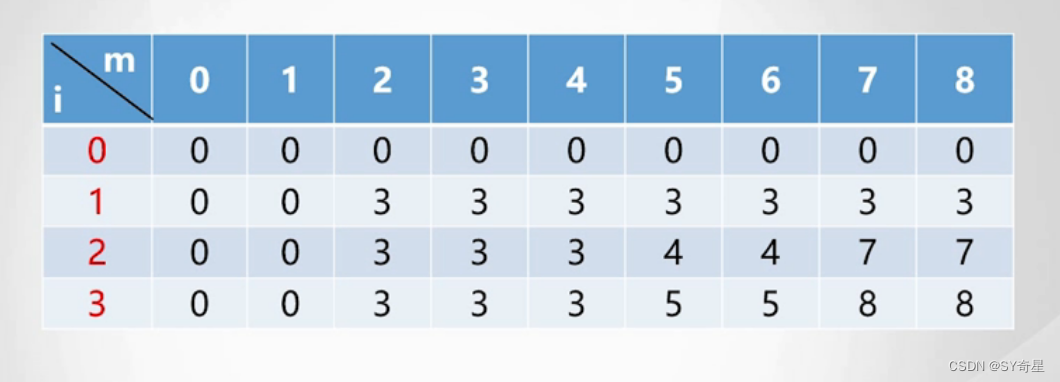
（三.核心代码）

//外遍历宝石数量 for(int i=1;i<=n;i++){//内遍历背包容量 for(int j=1;j<=m;j++){//装不下 if(j<w[i]){f[i][j]=f[i-1][j]; }//装得下 else{//状态转移方程 f[i][j]=max(f[i-1][j],f[i-1][j-w[i]]+c[i]); }}}

（四.【AC代码】）

#include<iostream>
using namespace std;
int w[1001],c[1001];  //分别表示物体重量和价值
int f[1001][1001];  //表示物体编号为i，背包容量为j时，最大价值 
int main(){int m,n;cin>>m>>n;for(int i=1;i<=n;i++){cin>>w[i]>>c[i];}//外遍历宝石数量 for(int i=1;i<=n;i++){//内遍历背包容量 for(int j=1;j<=m;j++){//装不下 if(j<w[i]){f[i][j]=f[i-1][j]; }//装得下 else{//状态转移方程 f[i][j]=max(f[i-1][j],f[i-1][j-w[i]]+c[i]); }}}//输出最优解cout<<f[n][m]; return 0;
}

三.买宝石

（一.题目）

1.1题目描述

假设我们有v(1 <v<25)种宝石，顾客需要价值n(1<n≤1000)元的宝石，刚好能买够n元的方案有多少种？

1.2输入输出描述

输入：

一个整数v表示有v种宝石，一个整数n表示有n元

v个整数分别表示每种宝石的价格

输出：

有多少种购买方案

1.3样例

输入:

3 8
1 2 5

输出：
7

（二.思路）

根据打表，可以找到边界和状态转移方程

说明：i为多少种宝石，j表示价值

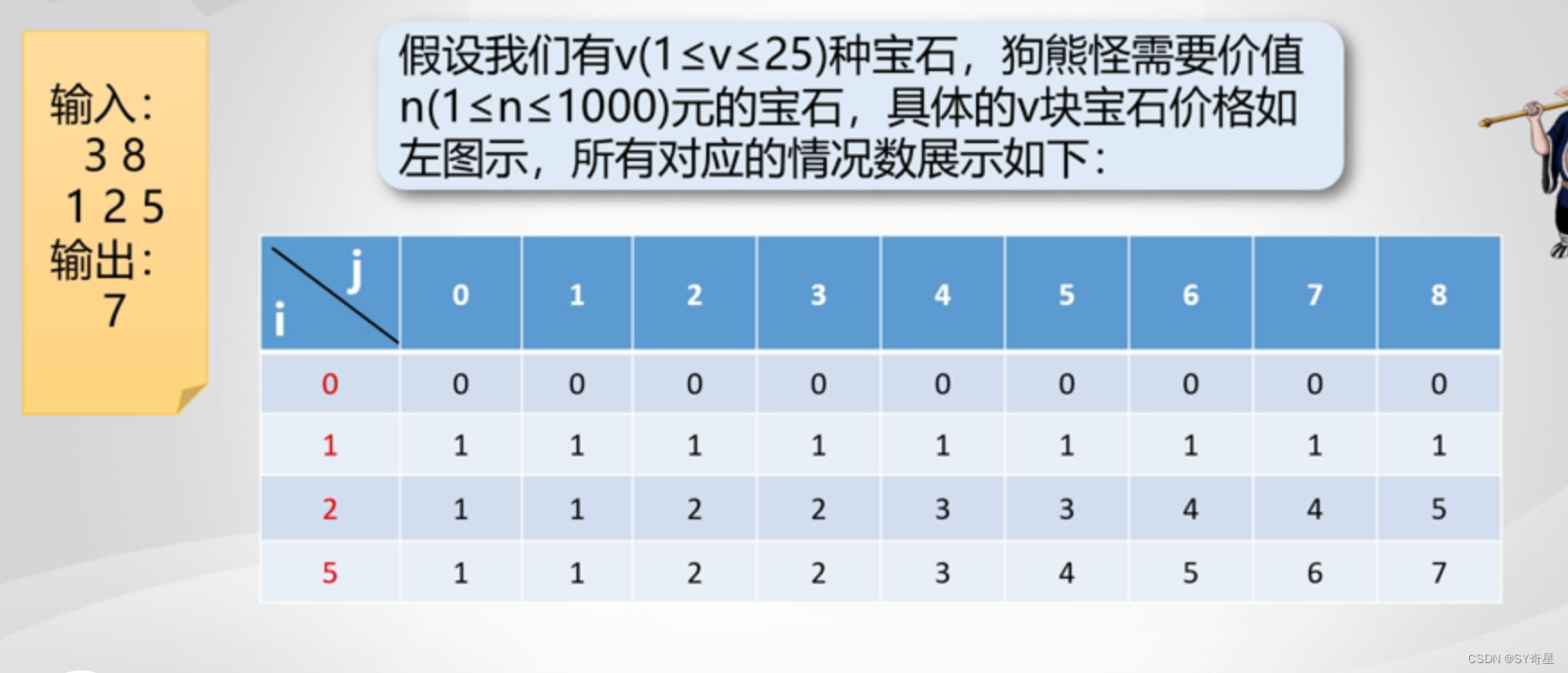
1.我们可以得到边界为：（1）f[0][j]=0,f[i][0]=1;

（2）if(i>1) for(j=0;j<p;j++) f[i][j]=f[i-1][j];

2. 我们得到状态转移方程为：f[i][j]=f[i-1][j]+f[i][j-p] //i为当前宝石的价格

（三.核心代码）

略

（四.【AC】代码）

#include<iostream>
using namespace std;
int v,n,p,i,j;
int f[1001][1001]; 
int main(){cin>>v>>n;for(i=1;i<=v;i++){cin>>p;//边界 f[i][0]=1;if(i>1){for(j=0;j<p;j++) f[i][j]=f[i-1][j];}//状态转移方程 for(j=p;j<=n;j++){f[i][j]=f[i-1][j]+f[i][j-p];}}cout<<f[v][n];return 0;
}