动态规划算法与典型例题

article/2025/10/7 3:56:44

前言

一、动态规划要素（条件）

二、动态规划算法设计步骤

三、复杂度分析

四、典型例题1——游艇租聘

五、典型例题2——0-1背包问题

六、典型例题3——跳台阶问题

七、典型例题4——强盗抢劫问题

总结

前言

动态规划也是一种分治思想，分治算法是把原问题分解为若干子问题，自顶向下求解子问题，合并子问题的解，从而得到原问题的解。动态规划是把原问题分解为若干子问题，自底向上，先求解子问题，把结果存储在表格中，在求解大问题时直接从表格中查询小问题的解，避免重复计算，从而提高算法效率。

一、动态规划要素（条件）

1.最优子结构，问题的最优解包括子问题的最优解。如果不具有最优子结构则不能使用动态规划。

2.子问题重叠，在求解子问题时有大量子问题是重复的，那么只需求解一次，然后把它存储到表格中，以后使用时直接查询，不需重复求解。子问题重叠不是使用动态规划的必要条件，但是只有存在子问题重叠才能彰显动态规划的优势。线

二、动态规划算法设计步骤

1.分析最优解的结构特征

2.建立最优值递归式

3.自底向上计算最优值，并记录

4.构造最优解

很多复杂的问题很难找到递归式，但是一旦找到递归式，那么算法已经实现99%。

三、复杂度分析

时间复杂度：一般为O(n), O(n^2), O(n^3)等n的整数方，看其需要几重循环。

空间复杂度：一般为O(1),O(n), O(n*m)等，看其子问题最优解与几个控制量有关。

四、典型例题1——游艇租聘

问题描述：长江游艇俱乐部在长江上设置了n个游艇租聘站，游客可以在这些租聘站租用游艇，然后在下游的任何一个租聘站归还。游艇出租站i到j的租金为r(i, j)，1 <= i< j<= n，设计一个算法，计算从出租站i到j所需的最少租金。

构造二维数组m[i][j]表示从出租站i到j的最少租金，那么两个子问题：(i, i+1, ... , k), (k, k+1, ..., j)最优值分别是m[i][k]和m[k][j]。

递归式：

$m[i][j]=\left\{\begin{matrix} 0 & ,j=i \\ r[i][j] &,j=i+1 \\ min \begin{Bmatrix} m[i][k]+m[k][j], r[i][j] \end{Bmatrix}& ,j > i+1 , i < k < j \end{matrix}\right.$

伪代码：

void rent()
{int i, j, k, d;for(d = 3, d <= n; ++d)//将问题分为小规模d。d=0时，租金为0；d=1时，租金为单站租金{for(i = 1; i <= n-d+1; ++i)//起点{j = i+d-1;//终点for(k = i+1; k < i+d-1; ++k)//换乘站，求解每一小规模子问题的解{int temp = m[i][k] + m[k][j];if(temp < m[i][j]) m[i][j] = temp;}}}
}

总体的求解过程为沿着主对角线一层一层向上，直到右上角填充完毕，则右上角值为所求解。

时间复杂度O(n^3)，空间复杂度O(n^2)。如果在原数组上更新计算值，则空间复杂度可以优化到O(1)。

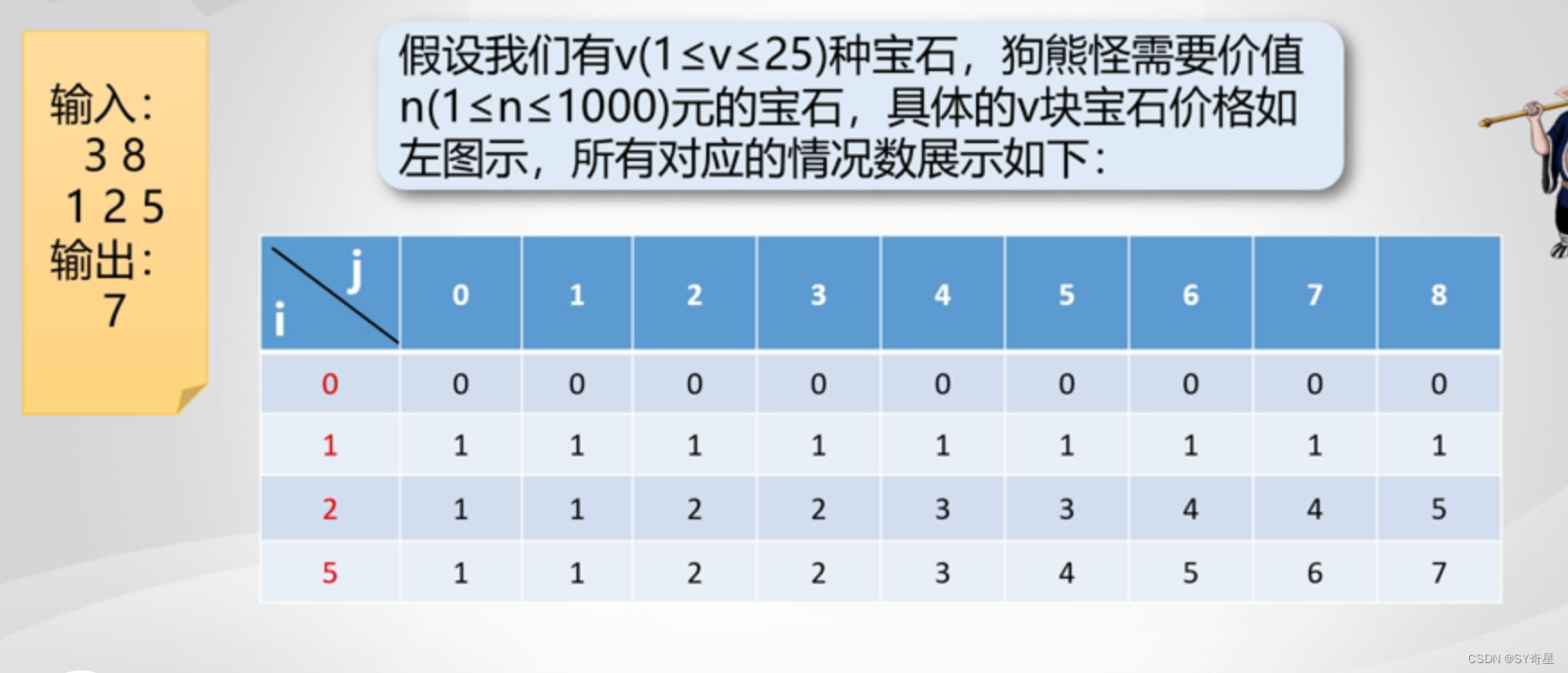
五、典型例题2——0-1背包问题

问题描述：动态规划针对不可切割物品，可切割物品可以使用贪心算法。

约束条件：

$\left\{\begin{matrix} \sum w_i*x_i \leqslant W&,1 \leqslant i \leqslant n \\ x_i\in \begin{Bmatrix} 0,1 \end{Bmatrix}& ,1 \leqslant i \leqslant n \end{matrix}\right.$

目标函数：

$max\sum v_i*x_i, 1 \leqslant i \leqslant n$

c[i][j]表示前i件物品放入容量为j的购物车可以获得的最大价值。

递归式：

$c[i][j]=\left\{\begin{matrix} c[i-1][j] &, j<w_i \\ max\begin{Bmatrix} c[i-1][j], c[i-1][j-w[i]]+v[i] \end{Bmatrix}& ,j\geqslant w_i \end{matrix}\right.$

for(int i = 1; i <= n; ++i)
{for(int j = 1; j <= w; ++j){if(j < w[i])//i物品重量大于购物车，则不放入{c[i][j] = c[i-1][j];}else{//比较i物品放入后能否让购物车价值最大c[i][j] = max(c[i-1][j], c[i-1][j-w[i]]+v[i]);}}
}

总体求解过程一层一层求解，右下角为所求解。

时间复杂度O(n*W)，空间复杂度O(n*W)。

六、典型例题3——跳台阶问题

问题描述：有 N 阶楼梯，每次可上一阶或两阶，求有多少种上楼梯的方法。

容易证明该递推式是斐波拉切数列，

$f(n) = n, n < 3$

$f(n)=f(n-1)+f(n-2), n\geqslant 3$

代码：

int jump(int n)
{if(n < 3) return n;int i = 1, j = 2, res = 0;for(int k = 0; k < n-2; ++k){res = i + j;i = j;j = res;}return res;
}

时间复杂度O(n)，空间复杂度O(1)。

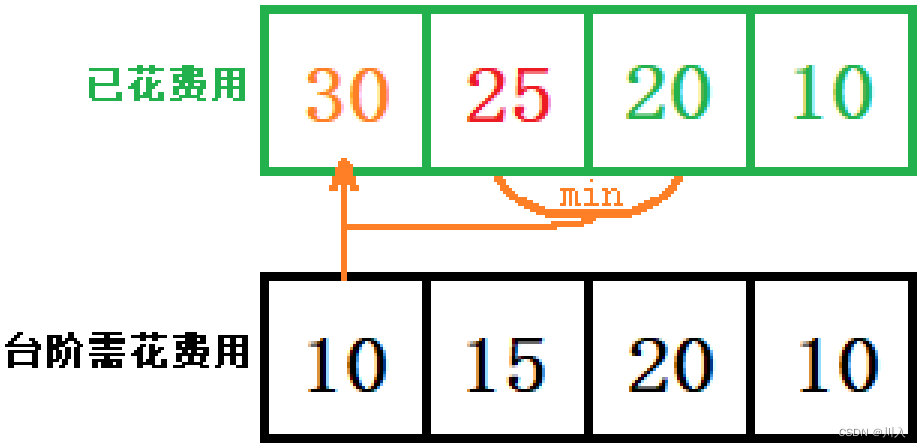
七、典型例题4——强盗抢劫问题

问题描述：强盗抢劫一排房间，每个房间都有钱，不能抢劫两个相邻的房间，要求抢的钱最多。

一维数组dp[i]是当抢到第i个数时，能抢到最大值，从局部最大值推到最终结果最大。

递归式：

$DP[i] = max(DP[i-2] + nums [ i ], DP[i-1])$

代码：

int robber(vector<int> &nums)
{int size = nums.size();if(size == 0) return 0;if(size == 1) return nums[0];vector<int> dp(size, 0);dp[0] = nums[0];dp[1] = nums[0] > nums[1] ? nums[0] : nums[1];for(int i = 2; i < size; ++i){dp[i] = max(dp[i-2] + nums[i], dp[i-1]);}return dp[size-1];
}

时间复杂度O(n)，空间复杂度O(n)。