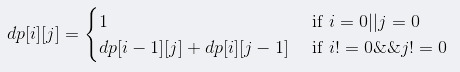动态规划入门请看:
DP动态规划专题(一)动态规划基本模型
前言
【说明】
关于动态规划的见解:动规和递归有很多相似的地方,最显著的特征可以说是阶段性,二者都有很明显的阶段划分,所以,声明好每一个阶段所需要做的事情以及阶段与阶段之间的转移可以说是重中之重了,这就涉及几个问题,第一,需要声明好方法(递归)或者数组(动规)具体的意义,所代表的作用;第二,需要说明好递归处理数据的方式(递归)或者是阶段转移方程(动规)。第三,跳出方法的条件(递归)或者是数组边界条件(动规)。处理好这三个方面,基本上就没有问题,剩下的就是一些边边角角的问题。
【提炼】
- 声明数组代表的含义
- 状态转移方程
- 边界条件
代码
1.数字金字塔
【题目】
观察下面的数字金字塔。写一个程序查找从最高点到底部任意处结束的路径,使路径经过数字的和最大。每一步可以从当前点走到左下方的点也可以到达右下方的点。
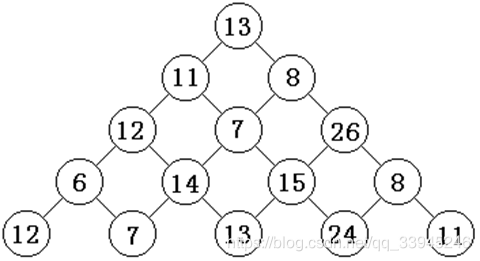
在上面的样例中,从13到8到26到15到24的路径产生了最大的和86。
【输入】:
第一个行包含R(1<= R<=1000),表示行的数目。
后面每行为这个数字金字塔特定行包含的整数。
所有的被供应的整数是非负的且不大于100。
【输出】:
单独的一行,包含那个可能得到的最大的和。
【样例输入】:
5 //数塔层数
13
11 8
12 7 26
6 14 15 8
12 7 13 24 11
【样例输出】:
86
【代码1】
/*** 顺推 dp* 含义:f[x][y] 从0,0到x,y最大值* 方程:f[x][y] = max{f[x-1][y],f[x-1][y-1]} + a[x][y]* 边界:f[0][0] = a[0][0]* */public int positive(int[][] a) {int[][] f = new int[a.length][a.length];// 边界f[0][0] = a[0][0];// 状态转移方程int i,j;for (i=1; i<a.length; i++) {for (j=0; j<=i; j++) {/*判断是否数组越界,左右两边需单独处理*/if (j == 0) {f[i][j] = f[i-1][j] + a[i][j];} else if (j == i) {f[i][j] = f[i-1][j-1] + a[i][j];} else {int max = f[i-1][j] > f[i-1][j-1] ? f[i-1][j] : f[i-1][j-1];f[i][j] = max + a[i][j];}}}// 获取最大值int temp = 0;for (i=0; i<a.length; i++) {if (f[a.length-1][i] > temp) {temp = f[a.length-1][i];}}return temp;}
【代码2】
/*** 逆推* 含义:f[x][y]表示从x,y到终点的最大值,所以f[0][0]即为所求* 公式:f[x][y] = max{f[x+1][y+1],f[x+1][y]} + a[x][y]* 边界:f[length-1][0...length-1] = a[length-1][0...length-1]* */public int negative(int[][] a) {int[][] f = new int[a.length][a.length];// 边界int i,j;for (i=0; i<a.length; i++) {f[a.length-1][i] = a[a.length-1][i];}// 状态转移for (i=a.length-2; i>=0; i--) {for (j=0; j<=i; j++) {int max = f[i+1][j+1] > f[i+1][j] ? f[i+1][j+1] : f[i+1][j];f[i][j] = max + a[i][j];}}return f[0][0];}
2.最长不下降子序列
㈠问题描述:
设有由n个不相同的整数组成的数列,记为:b(1)、b(2)、……、b(n)且b(i)<>b(j) (i<>j),若存在i1<i2<i3< … < ie 且有b(i1)<b(i2)< … <b(ie)则称为长度为e的不下降序列。程序要求,当原数列出之后,求出最长的不下降序列。
- 例如13,7,9,16,38,24,37,18,44,19,21,22,63,15。
- 例中13,16,18,19,21,22,63就是一个长度为7的不下降序列,
- 同时也有7 ,9,16,18,19,21,22,63长度为8的不下降序列。
㈡算法分析:
根据动态规划的原理,由后往前进行搜索(当然从前往后也一样)。
- 对b(n)来说,由于它是最后一个数,所以当从b(n)开始查找时,只存在长度为1的不下降序列;
- 若从b(n-1)开始查找,则存在下面的两种可能性:
①若b(n-1)<b(n)则存在长度为2的不下降序列b(n-1),b(n)。
②若b(n-1)>b(n)则存在长度为1的不下降序列b(n-1)或b(n)。 - 一般若从b(i)开始,此时最长不下降序列应该按下列方法求出:
在b(i+1),b(i+2),…,b(n)中,找出一个比b(i)大的且最长的不下降序列,作为它的后继。
㈢代码:
public class LongSubSequence {/*** 最长不下降子序列* 逆序* 含义:f[n]-从n到最后的最大长度;c[n]-存放下一个的下标* 公式:f[n] = max{f[x]} + 1;{x>n && a[n]<=a[x]}* 边界:f[a.length-1] = 1;* */public void negative(int[] a) {int length = a.length;int[] f = new int[length];int[] c = new int[length];// borderf[length-1] = 1;// formulaint i,j;for (i=length-2; i>=0; i--) {// 保存长度int l = 0;// 保存索引int k = 0;for (j=i+1; j<=length-1; j++) {if (l<f[j] && a[i]<=a[j]) {l = f[j];k = j;}}f[i] = l + 1;c[i] = k;}// resultint temp = 0;int index = 0;for (i=0; i<length; i++) {if (temp < f[i]) {temp = f[i];index = i;}}System.out.println("the long of sub sequence : " + temp);System.out.print("the sub sequence is : ");while (index != 0) {System.out.print(a[index] + " ");index = c[index];}}/*** 最长不下降子序列* 正序* 含义:f[n],从起点到当前的最大长度* 公式:f[n] = max{f[x]} + 1;{0<=x<n && a[x]<=a[n]}* 边界:f[0] = 1;* */public void positive(int[] a) {int length = a.length;int[] f = new int[length];int[] c = new int[length];// borderf[0] = 1;// formulaint i,j,l,k;for (i=1; i<length; i++) {l = 0;k = 0;for (j=0; j<i; j++) {if (l<f[j] && a[j]<=a[i]) {l = f[j];k = j;}}f[i] = l + 1;c[i] = k;}// resultint temp = 0;k = 0;for (i=0; i<length; i++) {if (temp < f[i]) {temp = f[i];k = i;}}System.out.println("the long of sub sequence : " + temp);System.out.print("the sub sequence is : ");while (k != 0) {System.out.print(a[k] + " ");k = c[k];}}public static void main(String[] args) {LongSubSequence l = new LongSubSequence();int[] a = new int[]{13,7,9,16,38,24,37,18,44,19,21,22,63,15};l.negative(a);System.out.println("");l.positive(a);}
}
3.走楼梯
【问题】
有 n 级台阶,一个人每次上一级或者两级,问有多少种走完 n 级台阶的方法
【解析】
本质上是斐波那契数列问题
假设只有一个台阶,那么只有一种跳法,那就是一次跳一级,f (1)=1;如果有两个台阶,那么有两种跳法,第一种跳法是一次跳一级,第二种跳法是一次跳两级,f (2)=2。如果有大于 2 级的 n 级台阶,那么假如第一次跳一级台阶,剩下还有 n-1 级台阶,有 f (n-1) 种跳法,假如第一次条 2 级台阶,剩下 n-2 级台阶,有 f (n-2) 种跳法。这就表示 f (n)=f (n-1)+f (n-2)
【代码】
/*** 有 n 级台阶,一个人每次上一级或者两级,问有多少种走完 n 级台阶的方法* 含义:f[n]-走法个数* 公式:f[n] = f[n-1] + f[n-2]* 公式代表第一步走一阶,则有f[n-1],第一步走二阶,则有f[n-2]* */public int positive(int n) {if (n == 1) {return 1;} else if (n == 2) {return 2;} else {int[] f = new int[n+1];f[1] = 1;f[2] = 2;for (int i = 3; i<=n; i++) {f[i] = f[i-1] + f[i-2];}return f[n];}}
4.公共子序列
【问题描述】
一个给定序列的子序列是在该序列中删去若干元素后得到的序列。确切地说,若给定序列X=<x1,x2,…,xm>,则另一序列Z=<z1,z2,…,zk>是X的子序列是指存在一个严格递增的下标序列<i1,i2,…,ik>,使得对于所有j=1,2,…,k有:
Xij=Zj
例如,序列Z=<B,C,D,B>是序列X=<A,B,C,B,D,A,B>的子序列,相应的递增下标序列为<2,3,5,7>。给定两个序列X和Y,当另一序列Z既是X的子序列又是Y的子序列时,称Z是序列X和Y的公共子序列。例如,若X=<A,B,C,B,D,A,B>和Y=<B,D,C,A,B,A>,则序列<B,C,A>是X和Y的一个公共子序列,序列 <B,C,B,A>也是X和Y的一个公共子序列。而且,后者是X和Y的一个最长公共子序列.因为X和Y没有长度大于4的公共子序列。
给定两个序列X=<x1,x2,…,xm>和Y=<y1,y2….yn>.要求找出X和Y的一个最长公共子序列。
【样例输入】
ABCBDAB
BDCABA
【样例输出】
4
【代码】
/*** @author 谢世杰*/
public class LongCommonSequence {/*** 顺序* 两个序列的最长公共子序列** 含义:f[x][y],A序列0...x 和 B序列0...y 的公共子序列最大长度** 分四种情况考虑:* 1.A[x]在公共子序列,B[y]不在,则f[x][y] = f[x][y-1]* 2.A[x]不在公共子序列,B[y]在,则f[x][y] = f[x-1][y]* 3.A[x],B[y]均在,则f[x][y] = f[x-1][y-1] + 1* 4.A[x],B[y]均不在,则f[x][y] = f[x-1][y-1]* 则 f[x][y] 取上述最大值即可,f[x-1][y-1]和f[x-1][y-1]+1 可以合并为后者** 公式:f[x][y] = max{f[x][y-1],f[x-1][y],f[x-1][y-1]+1}* 边界:f[0...x][0] = 0, f[0][0...y] = 0* */public void method(char[] a, char[] b) {int na = a.length;int nb = b.length;int[][] f = new int[na+1][nb+1];// 公式int i,j;for (i=1; i<=na; i++) {for (j=1; j<=nb; j++) {// 考虑a,b中有一个是在目标子串中f[i][j] = f[i-1][j] > f[i][j-1] ? f[i-1][j] : f[i][j-1];// 当a,b都在目标子串中if (a[i-1] == b[j-1]) {f[i][j] = (f[i-1][j-1] + 1) > f[i][j] ? (f[i-1][j-1] + 1) : f[i][j];}}}System.out.println("long = " + f[na][nb]);}public static void main(String[] args) {LongCommonSequence l = new LongCommonSequence();String a = "ABCBDAB";char[] aa = a.toCharArray();String b = "BDCABA";char[] bb = b.toCharArray();l.method(aa,bb);}
}