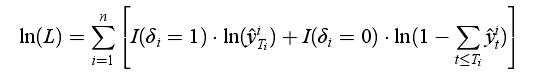python做生存分析

article/2025/10/26 20:56:53

这里跟大家分享一下生存分析，并且介绍一个用python做生存分析的包。

生存分析

应用场景

生存分析最早在生物医学中使用的最多，用来预估某个群体的存活时间，后来被推广到了更广泛的领域。一个做生物的专家可能通常会关心这样一个问题：这个群体的样本能活多久？这个问题我们通常会使用生存分析来回答。这个群体可以理解为某个国家的人民，或者注射过某种药物的一些病人。

同样也可以推广到更一般的场景，公司的客户流失情况，一个用户开始接受他们的服务可以认为是一个样本的出生，一个客户的离开可以认为是一个样本的死亡。比如我去年办了一张移动电话卡，现在突然不想用了去注销掉了。用户流失情况分析等问题很多电商平台也十分关注。

截断

以样本的出生和死亡为例，我们观测一组样本的生存时间。然而我们观测和追踪他们是需要时间和金钱的成本的，不可能因为样本一直存活着，我们就一直将某个实验做下去。通常，专家只会对一组样本观测一段时间，例如，两年或者两个月。有些样本在观测期间触发了目标事件（death），而有些样本直到实验观测结束也没有触发目标事件，我们称没有触发目标事件的样本有右侧截断。

NOTE：同样也存在左侧截断和中间截断，我们稍后再说。

一个常见的错误是人们可能在评估目标群体存活时间时会简单的忽略右侧截断，我们首先来看一下这会导致什么问题：

考虑这样一个例子：我们观测的目标人群实际上是来自两个不同的组（可以简单理解为患了不同的病），他们的平均存活时间是不一样的，假定A组的平均存活时间只有两个月，而B组的平均存活时间有十二个月。值得注意的是我们现在是把他们全部放在一起观测的，我们并不知道谁是A组谁是B组，而我们的目的是想知道这些人平均会活多久。假定我们的实验进行了十个月就结束了。

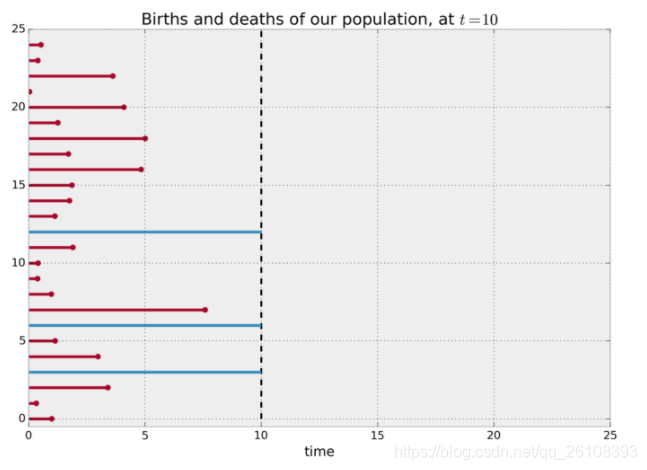
如果我们只是简单地删除那些发生右侧截断的样本，然后对所有人的生存时间求平均，我们将会严重低估这个群体的生存时间。

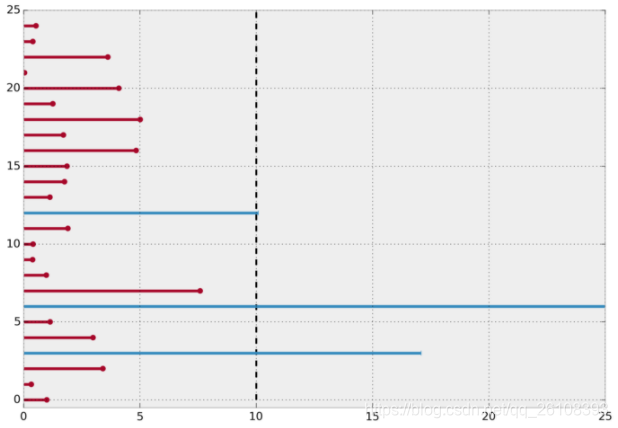
如果我们不删除发生右侧截断的样本而直接求平均值，仍然会低估这个群体的平均生存时间，要注意的是，我们只能观测到10时刻之前的事情，10时刻之后的我们并不能看到。

生存分析最初被设计出来的目的就是为了处理存在右侧截断的这种数据的。但是，即使我们的数据不包含右侧截断，生存分析仍然是一个强大有效的工具。

上述例子是为了阐述方便所以让所有的样本的出生从0时刻开始，而实际上这是不必要的，生存分析并不要求所有样本在同一时刻出生，它只关注每个样本从出生到death触发或到实验结束之间的间隔时间，每个样本随时可以出生。

生存函数

我们设 $T$ 是一个随机变量，它表示一个样本的从出生到死亡所经历的时间。T总是大于0的，有可能是无穷。对一个群体，我们定义生存函数 $S(t)$ 如下：

$S(t)=Pr(T>t)$

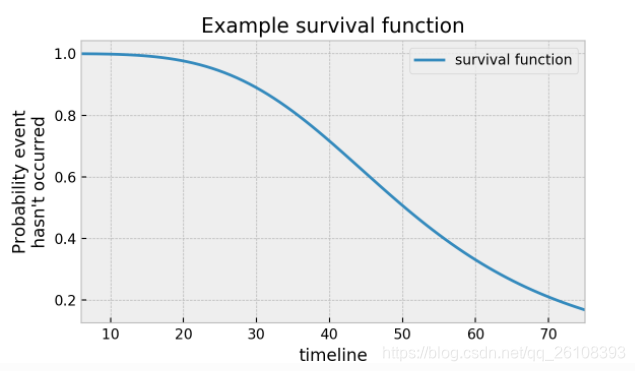
解释： $S(t)$ 描述了这个群体的样本生存时间大于 $t$ 的概率，换句话说，直到时刻 $t$ ,我们仍然没有观测到death事件的发生。

它有以下几个性质：

$0\leq S(t) \leq 1$ 。
$F_T(t)=1-S(t)$ , $F_T$ 是随机变量 $T$ 的累积分布函数。
$S(t)$ 是一个单调不增的函数。

$S(t)$ 的函数图像可能是下面这个样子：

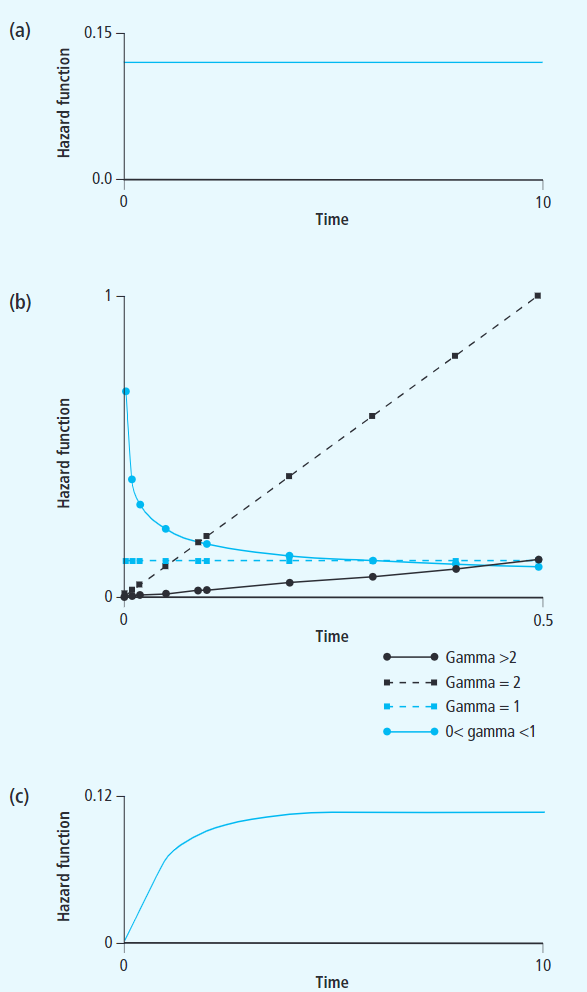
风险函数

我们同样可能会关心某个样本在 $t$ 时刻死亡的概率，也就是说，直到 $t$ 时刻我们都没有观察到该样本的死亡，而在 $t$ 时刻的一个右邻域观察到该样本死亡。即：

$\mathop{lim}\limits_{\delta t\rightarrow 0} Pr(t\leq T\leq t+\delta t |T>t)$

由于上述极限随着 $\delta t$ 的减小而趋于0，我们定义

$h(t)=\mathop{lim}\limits_{\delta t\rightarrow 0} \frac{Pr(t\leq T\leq t+\delta t |T>t)}{\delta t}$

等价地，有：

$h(t)=\frac{-S'(t)}{S(t)}$

这是一个变量可分离的微分方程：

$z(x)=- \frac{1}{y} \frac{dy}{dx} \Rightarrow z(x)dx= -\frac{1}{y}dy$

因此，我们分离变量后，两遍同时取积分，并注意到 $S(0)=1$

可以解得 $S(t)=exp(-\int_{0}^{t} h(x)dx)$

其中的积分部分有一个更为一般的名称，我们称 $H(x)=\int_{0}^{t} h(x)dx$ 为累积风险函数。

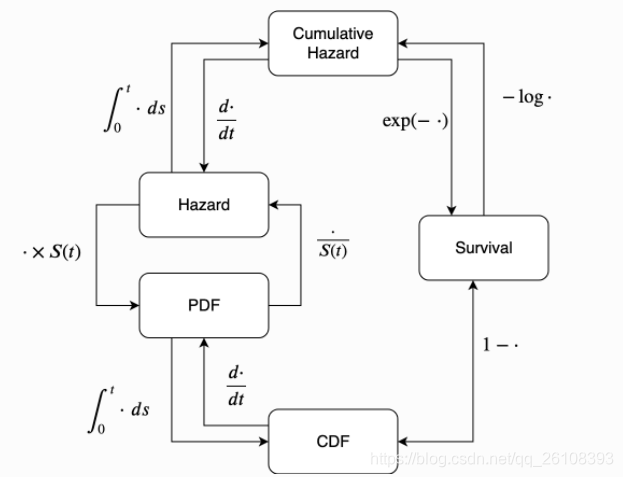
这张图表示了这些函数之间的关系。

估计生存函数

而我们在实践中是不可能知道真实的生存函数的，只能去对它进行估计。

于是，我们接下来的问题就变成了如何对生存函数进行估计。

接下来就是大家经常听到的Kaplan-Meier Estimate、Nelson-Aalen Estimate等估计方法。

这里以Kaplan-Meier为例：

Kaplan-Meier是一种非参数的估计方法。

简单说一下非参数估计和参数估计

参数估计：我们通过一定的基本假设和建模获得了待估计函数的形式，而有若干控制该函数具体表现的参数。而我们的目的是从形式已知参数未知的模型簇里找出合适的参数。把这个函数当做我们对目标函数的估计。

非参数估计：我们并不对待估计的函数形式做任何假设，而是直接从数据出发去估计它。

优缺点：在数据量较小的时候，参数估计的表现会比较好。而非参数估计会由于数据量有限而无法表现出良好的性能。在数据量充足的时候，非参数估计由于减少了强加给数据的假设而会表现的比参数估计好。通常非参数估计的计算量大于参数估计。

$\hat{S(t)}=\prod_{ti<t} \frac{n_i-d_i}{n_i}$