生存分析基础知识

生存分析

定义：将事件结局的出现与否和达到终点所经历的时间结合起来的 统计方法
背景：对于癌症患者，更加关注“生存时间”，比如常常听到的：5年存活率、3年存活率……，且某种治疗方法的价值主要表现在延长患者的存活时间。
比如在一项针对癌症患者的研究中，研究者更加关注的问题在观测时间点发生特定事件的概率，寻找个体协变量与个体生存状态之间的潜在关系（观测时间和观测事件状态）

• 癌症患者在接受治疗后的生存状况如何
• 哪种疗法的效果更好
• 这些患者在接受治疗后的生存状况与哪些因素有关

事件
生存时间
删失问题

生存数据

1. 兼有时间和结局两种属性的数据，生存数据表示集合A={($x_i$,$T_i$,${\delta }_i$)|i=1,…,n}
   n表示数据中观测个数的数目 $x_i$ 是维度为m的向量，表示第i个个体的协变量 Ti表示该个体最后一次的观测时间（末次随访时间）
   ${\delta }_i$$\in${0,1}表示在Ti时刻是否观察到该个体有感兴趣的事件发生。
   令Te表示感兴趣的事件的研究终点，则患者集合{i|Ti<Te，${\delta }_i$=0}表示右删失的个体集合，即在研究终点之前的最后一次观测未观测到发生事件。
2. 结局为二分类互斥事件
3. 一般是通过随访收集得到，随访观察往往是从某统一时间点(如入院或实施手术等某种处理措施后)开始，观察到某规定时间点截止。
4. 常因失访等原因造成研究对象的生存时间数据不完整，分布类型复杂，不能简中地套用以前的缺失值处理方法。

生存函数

1.描述性

生存函数(survival function)：S(t)=Pr(T>t)表示生存时间T超过t的概率，定义了直到t时刻还未发生死亡（或interest感兴趣的事件）的概率

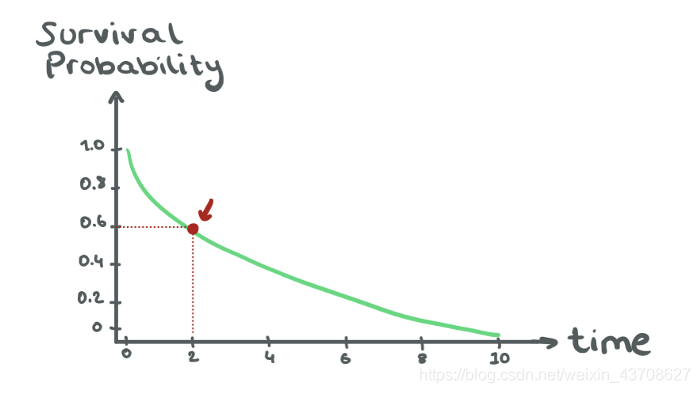
累积死亡函数 即Pr(T$\le$t)，其意义是对象存活时间不超过某一时间t的概率值。它是时间T分布的累计分布函数，F(t) = 1-S(t)
死亡概率分布 是累计分布的导数，意义是对象在某一时刻t的一瞬间死亡的概率

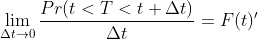
风险率 比如t时刻之前有100个存活病人，t时刻一瞬间有10个人死亡，这时候风险率是1/10，Cox模型的因变量就是风险率值，精确的定义为

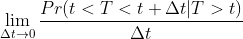
它与死亡概率函数的定义是有区别的，多了一个条件T>t
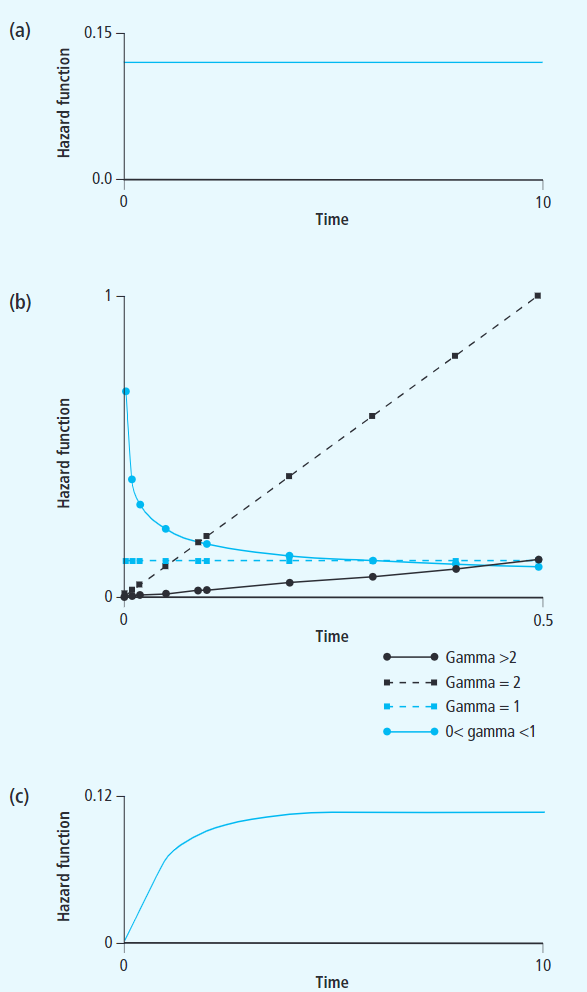
风险函数(hazard function)：定义了在生存时间大于t的条件下在t时刻发生事件的概率，不是密度也不是概率，可以看作是在t和t+dt之间的一个无限小的时间段内失败的概率，假定受试者一直存活到时间t。故t时刻的风险函数h(t)可以表示为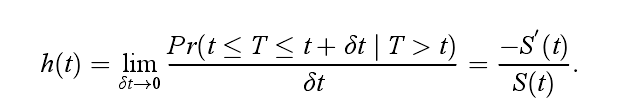
因此，生存函数S(t)与风险函数h(t)之间的关系如下

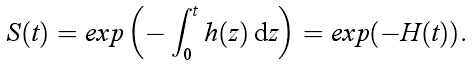
其中，H(t) = ${\int }_0^{t}h(z)dz$表示累计风险函数（Cumulative hazard function）。首次发生事件时间的概率密度函数f(t)为其累积分布函数F(t)对事件的导数，所以推导得到

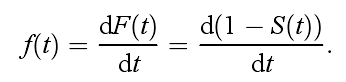
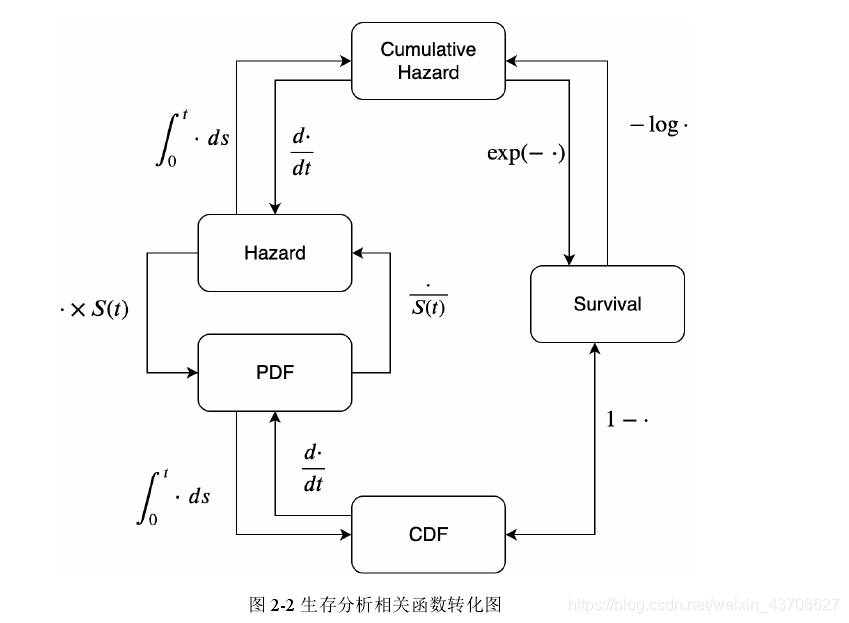
生存分析中的生存函数S(t)、风险函数h(t)、累积风险函数H(t)、首次发生事件时间的概率密度函数f(t)及其累积分布函数F(t)都可以通过上述公式相互转化得到

生存分析方法

生存分析统计方法

参数估计与非参数估计
参数估计：我们通过一定的基本假设和建模获得了待估计函数的形式，而有若干控制该函数具体表现的参数。而我们的目的是从形式已知参数未知的模型簇里找出合适的参数。把这个函数当做我们对目标函数的估计。
非参数估计：我们并不对待估计的函数形式做任何假设，而是直接从数据出发去估计它。

非参数方法

非参数的统计生存方法一般只用于直观理解研究对象的整体生存状态，如生存率和风险趋势等，不能用于个性化预测
Kaplan-Meier估计方法
Nelson-Aalen估计方法

半参数方法

考虑了个体协变量对个体生存状态的影响，使用线性模型预测个体的生存状态。

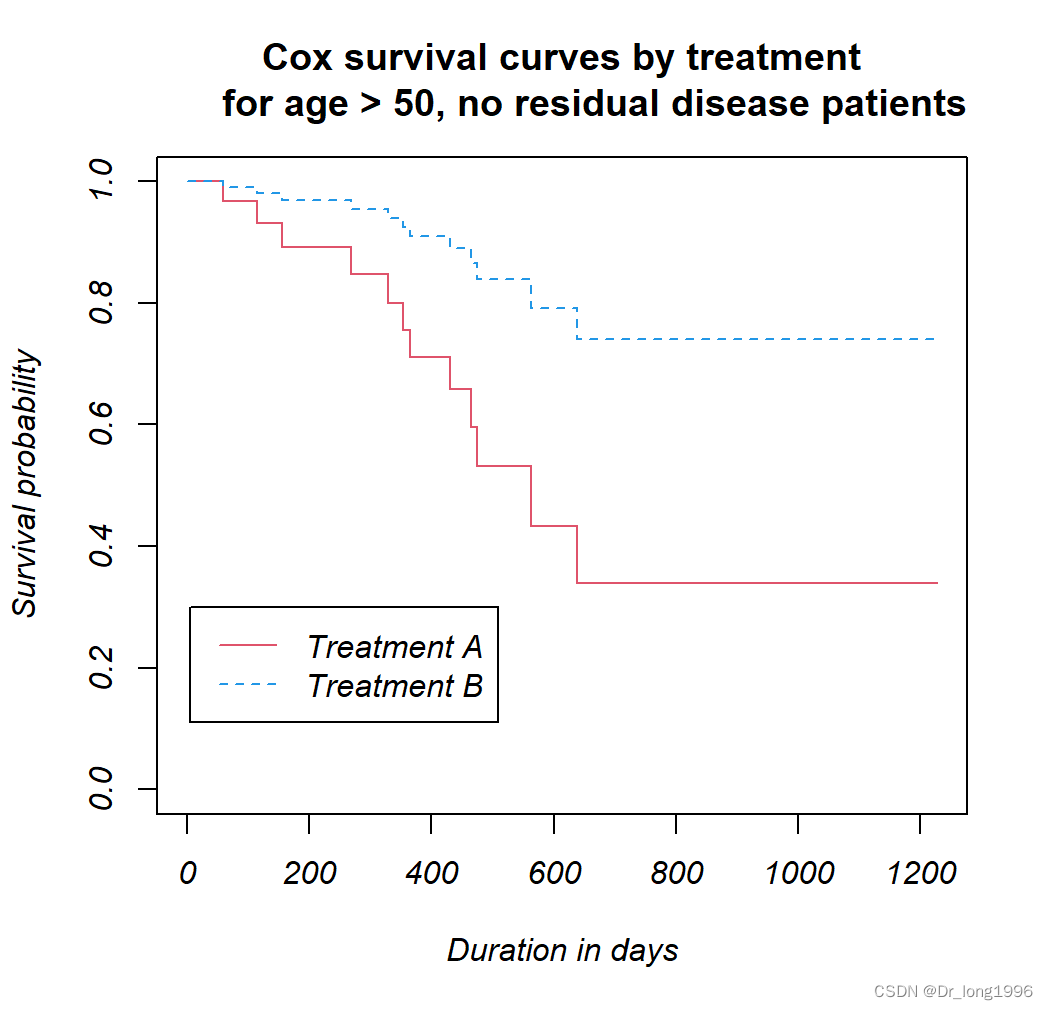
• Cox比例风险模型，本质上是一个线性模型，假设个体的风险函数与人群的基准函数之比为一个不随时间改变的常数。使用生存数据拟合Cox比例风险模型后，可以通过向模型输入个体协变量来预测其对数风险比例，然后使用下述公式估计该个体的生存函数。类似logistic回归，多个变量对Y的影响，得到一个概率值，只不过加了时间
  
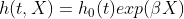
  前半部分是基线风险函数，不需要特定分布，是非参数
  后半部分相当于对多重线性回归的输出进行了次方变换，保证了正值和单调性
  参数说明：
  1.$h_o(t):$风险基准函数，就是引子中提到的关于时间t的函数，这个函数只与时间t有关，与特征X无关，并且该模型中没有给出风险基准函数的基本形式，只要满足非负连续即可，当 $\beta X$ 为0时，Cox模型只与风险基准函数有关。
  2.$X:$是引子中提到的主观因素，在Cox模型中叫做协变量，不同的研究个体有不同的协变量，从公式中可以看出他对于风险率是有影响的。
  3.$\beta$:协参数，类似线性回归里的参数向量，他也是一个向量，向量的长度同主观因素的个数是相同的（类似线性回归特征个数和参数个数相同），我们建立模型过程大部分的精力就是放在求解协参数β上，求解用到了部分似然估计
  参数估计：对偏似然函数，采用极大似然估计，使得当前样本出现的概率最大。
  抛开公式 假设研究某个对象在时间t的生存概率，影响生存概率的因素可以总结为两大类，一是时间，二是主观因素。
  时间：
  主观因素：一个
  随着时间的推移，死亡概率一定会不断增大，同时受到主观因素的制约，至于该主观因素是提高死亡率还是降低死亡率，每个个体情况并不相同。
  生存分析之Cox模型简述与参数求解: link.

• 另一种半参数线性预测模型是ThresReg，主要研究事件首次发生事件FHT(First Hitting Time)，与Cox比例风险模型不同的是，假设个体的风险函数是某个固定形式的带参数的随机过程，而不再是一个不随时间变化的风险比例
  
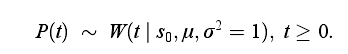
  其中，随机过程P(t)是一个维纳过程（Wiener Process），它含有初始状态参数$S_0$和模型参数$\mu$，这些参数和协变量通过链接函数ln($s_0$)=${\lambda }_1^{T}x$,$\mu ={\lambda }_1^{T}x$建立联系。参数${\lambda }_1,{\lambda }_2\in {\mathbb{R}}^m$通过极大化的下式所示的对数似然估计函数估计得到
  
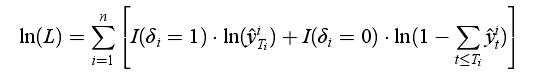
  其中${\hat{y}}_t^i$表示FHT模型预测的个体i在t时刻首次发生事件的概率，I()表示指示性函数，FTF模型的输出最终为个体首次发生事件时间的概率分布

参数方法

线性回归和加速失效模型，基于各种分布假设直接研究生存函数，这一类可以用于预测个体生存函数的全参数模型也是线性模型，同样需要承受线性模型带来的限制。

生存分析机器学习模型

传统模型为线性模型，基于机器学习的模型来学习生存数据中协变量与生存状态之间的非线性关系，常见的机器学习模型主要包括 支持向量机、决策树模型和深度神经网络等。

生存分析研究的内容

1.描述生存过程

研究生存时间的分布特点（可按照年龄、性别等分组），比较不同组件的分布特点，估计生存率及平均存活时间，绘制生存曲线等，根据生存时间的长短，可以估算出各个时点的生存率，并根据生存率来估计中位生存时间，也可以根据生存曲线分析其生存特点，一般使用Kaplan-Meier法和寿命表法。
　　Kaplan-Meier法：

2.比较生存过程

可通过生存率及其标准误对各样本的生存率进行比较，以探讨各组间的生存过程是否存在差异，一般使用Log-rank检验和Breslow检验。

3.分析危险因素

是通过生存分析模型来探讨影响生存时间和终点事件的保护因素和不利因素，因素作用的大小及方向，相对危险度的大小，基本使用Cox回归模型。

4.建立数学模型

建立最终的数学模型，也是通过Cox回归模型完成。

研究思路

1.数据

数据集的选取、预处理、数据分布
收集patient的个人信息、临床信息，处理得到模型规定的输入特征
进行表示学习：采用深度学习方法

2.模型设计

复发预后模型设计？？？
将患者的特征输入至上述建立好的模型，讲过模型内部的判断、计算、决策，输出模型对患者复发概率的估计值
两种策略：

• sole prediction：一次性预测，结果为二分类，发生或者不发生。输入：五年的生存数据，输出：第五年的生存结果
• probability dependence on time：随时间变化的概率。输入：五年的生存数据，输出：

3.实验部分（对比分析）

4.可解释性

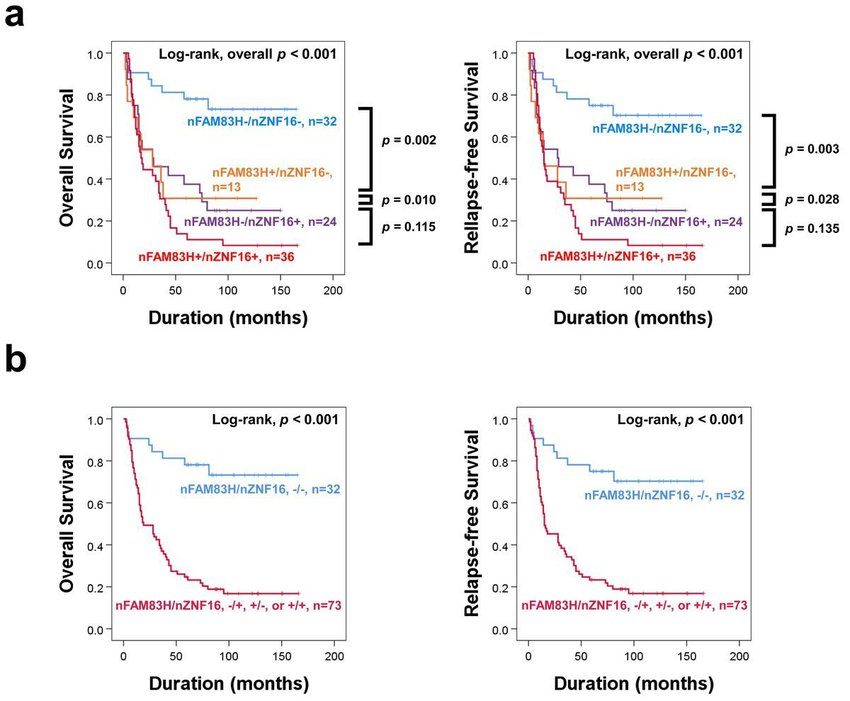
首先，使用Kaplan-Meier方法估计整个数据集人群总体的生存曲线
建立预后模型，应用：当患者完成初次诊断后，可以收集其个人信息和临床信息，整理得到模型规定的输入特征，然后，将患者的特征输入至上述建立好的早期癌症患者复发预后模型，经过该预后模型内部的判断、计算、决策、输出预后模型对该患者初次诊断后复发概率的估计值。最后，由模型给出的复发概率估计值，经过转化得到该患者的估计生存曲线。该曲线刻画了不同随访时长内，该患者生存（即未出现复发）的概率。最终，医生可以参考由早期乳腺癌患者复发预后模型给出的生存曲线估计，解读该患者5年内出现复发的概率，或者了解该患者的复发风险趋势，从而结合实际情况制定治疗方案或进行提前干预以减轻患者的负担。
因子分析
重要性排序，在进行模型建立后，使用该模型寻找对早期乳腺癌患者初次诊断后复发有重要影响的因子，或者探究不同因子的影响模式，即模型特征解释性在实际生存分析应用中是被要求的。
治疗推荐