1 KM法计算生存率——非参数模型

乘积极限法适用于离散数据，它用于建立时刻 $t$ 上的生存函数，根据 $t$ 时刻之前的所有时期的生存概率的乘积，来估计时刻 $t$ 的生存函数 $S(t)$和它的标准误 $SE(S(t))$ 。
生存概率 P ：观察对象活过某个时期的概率。
$$P=1-d/n$$

• $d$ ：期内死亡人数
• $n$：期初观察人数

生存率$\mathbf{S}({\mathbf{t}}_{\mathbf{i}})$：观察对象从起始时刻 $t_0$ 到 $t_i$ 时刻活过多个时期的概率。
$$\hat{S}(t_i)=\prod _{j=1}^i{p}_j,j=1,2,\cdots ,i$$
生存率标准误：
$$SE(\hat{S}(t_i))=\hat{S}(t_i)\sqrt{\sum _{j=1}^i\frac{d_j}{n_j(n_j-d_j)}},j=1,2,\cdots ,i$$
置信区间： 通常取 95% 置信区间 $u_{\alpha /2}=1.96$
$$\hat{S}(t_i)\pm u_{\alpha /2}\cdot SE(\hat{S}(t_i))$$
实例：

• 使用肺癌患者数据集，计算生存率。

  library(DT)
  library(survival) 
  datatable(lung)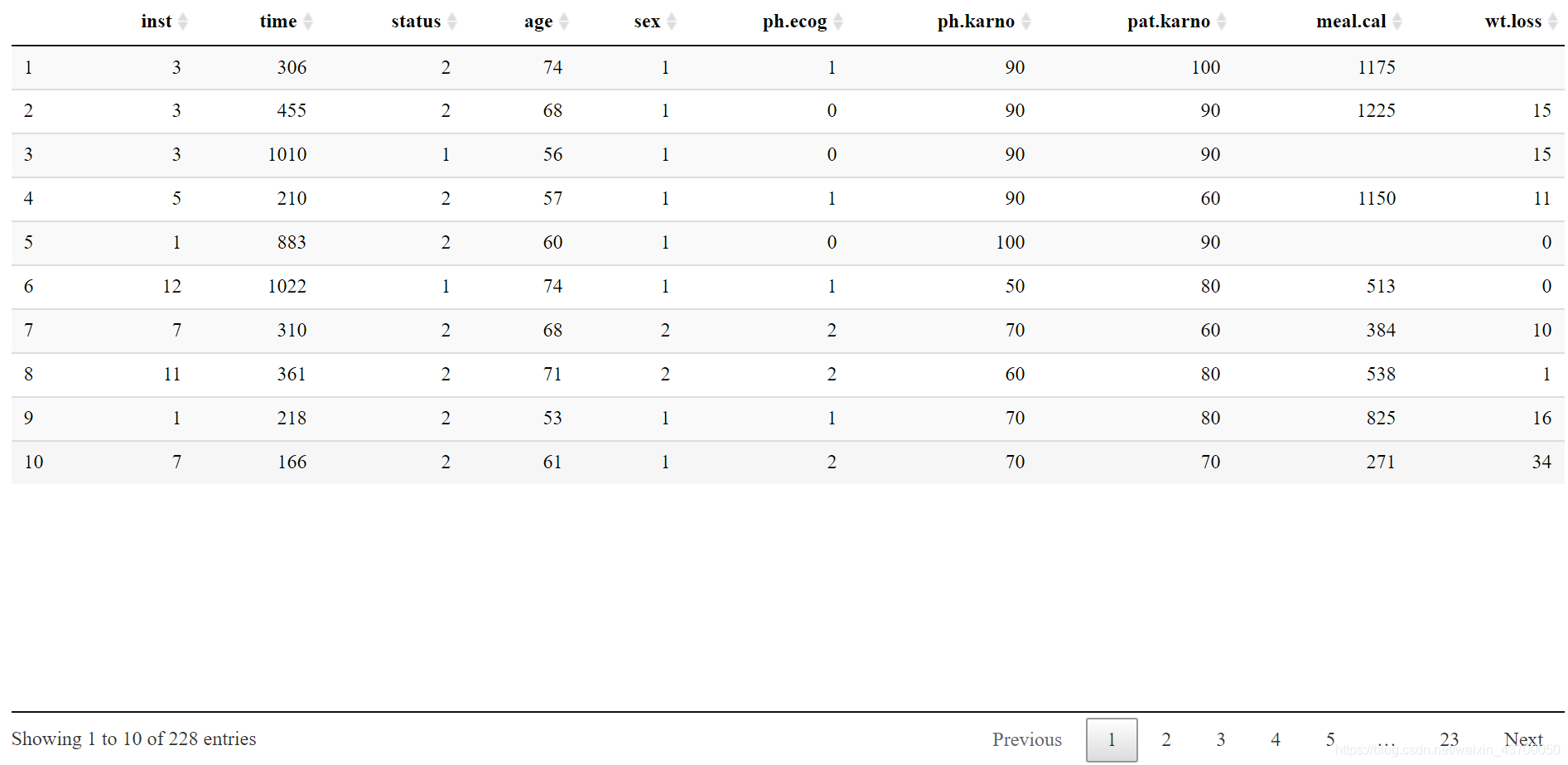
  

  
  数据集中time表示生存时间，status表示生存状态，1表示存活，为截尾数据，2表示死亡，为完整数据。
  用 survival 包来进行生存分析，survfit()函数计算生存率，surv()函数对生存时间进行排序，并将存活的患者生存时间改为截尾数据，用 + 号表示。

  fit = survfit(Surv(time,status)~1,data = lung) # ~1表示不对数据分组
  summary(fit)
  

  部分结果：
  
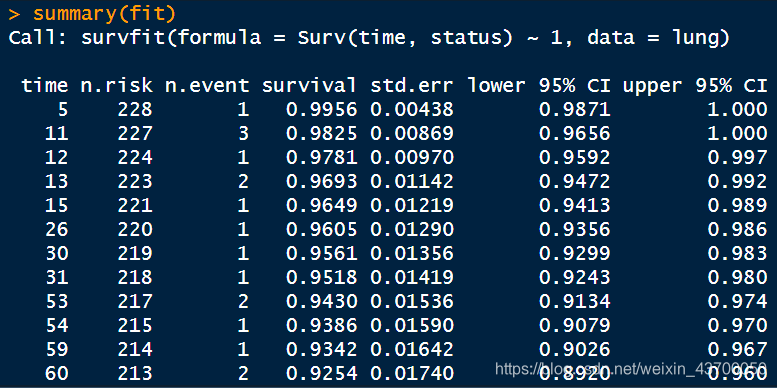
  上图中：

  • time：生存时间
  • n.risk：期初观察人数
  • n.event：期内死亡人数
  • survival：生存率
  • std.err：生存率标准误
  • lower 95% CI：95% 置信区间下界
  • upper 95% CI：95% 置信区间上界

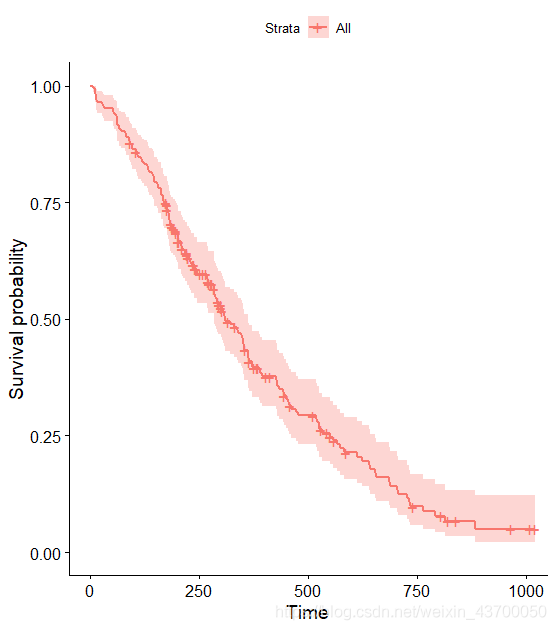
  可视化：

  library(survminer)
  ggsurvplot(fit,lung)
  

2 log-rank秩检验比较不同组的生存率

2.1 输入数据

取 lung 数据集前 20 行作为输入数据。

df = lung[1:20,]
head(df)

 inst time status age sex ph.ecog ph.karno pat.karno meal.cal wt.loss
1    3  306      2  74   1       1       90       100     1175      NA
2    3  455      2  68   1       0       90        90     1225      15
3    3 1010      1  56   1       0       90        90       NA      15
4    5  210      2  57   1       1       90        60     1150      11
5    1  883      2  60   1       0      100        90       NA       0
6   12 1022      1  74   1       1       50        80      513       0

2.2 建立假设

$H_0$: 男性患者和女性患者的生存率相同
$H_1$: 男性患者和女性患者的生存率不同
检验水准：$\alpha =0.05$

2.3 log-rank秩精确性检验

序号	时间（天）		Male			Female		all_n	all_d
		$n_{1i}$	$d_{1i}$	$T_{1i}$	$n_{2i}$	$d_{2i}$	$T_{2i}$	$n_i$	$d_i$
1	61	15	0	0.75	5	1	0.25	20	1
2	71	15	1	0.7894737	4	0	0.2105263	19	1
3	88	14	1	0.7777778	4	0	0.2222222	18	1
4	144	13	1	0.7647059	4	0	0.2352941	17	1
5	166	12	1	0.75	4	0	0.2500000	16	1
6	170	11	1	0.7333333	4	0	0.2666667	15	1
7	210	10	1	0.7142857	4	0	0.2857143	14	1
8	218	9	1	0.6923077	4	0	0.3076923	13	1
9	306	8	1	0.6666667	4	0	0.3333333	12	1
10	310	7	0	0.6363636	4	1	0.3636364	11	1
11	361	7	0	0.7000000	3	1	0.3	10	1
12	455	7	1	0.7777778	2	0	0.2222222	9	1
13	567	6	1	0.7500000	2	0	0.2500000	8	1
14	613	5	1	0.7142857	2	0	0.2857143	7	1
15	654	4	0	0.6666667	2	1	0.3333333	6	1
16	707	4	1	0.8000000	1	0	0.2000000	5	1
17	728	3	0	0.7500000	1	1	0.25	4	1
18	883	3	1	1	0	0	0	3	1
19	1010	2	0	0	0	0	0	2	0
20	1022	2	0	0	0	0	0	2	0

卡方计算:
$$\begin{gathered} V_{ki}=\frac{n_{ki}}{n_i}(1-\frac{n_{ki}}{n_i})(\frac{n_i-d_i}{n_i-1})d_i \\ {\chi }^2=2\cdot \frac{(\sum d_{ki}-\sum T_{ki}{)}^2}{\sum V_{ki}} \end{gathered}$$

n1_i = c(15,15,14,13,12,11,10,9,8,7,7,7,6,5,4,4,3,3,2,2)
n_i = c(rev(2:20),2)
d_i = c(rep(1,18),rep(0,2))
T1_i = d_i/n_i*n1_i
d1_i = c(0,1,1,1,1,1,1,1,1,0,0,1,1,1,0,1,0,1,0,0)sum1 = (sum(d1_i)-sum(T1_i))^2
sumVk = sum((n1_i/n_i)*(1 - n1_i/n_i) * (n_i- d_i)/(n_i-1) * d_i)chisq = 2*sum1/sumVk
chisq

[1] 0.1138165

经过计算： ${\chi }^2\approx 0.1$ ，查表得 $P\approx 0.8$
通常用 survival 包中 survdiff()函数计算$P$值：

survdiff(Surv(time,status)~sex,data = df)

Call:
survdiff(formula = Surv(time, status) ~ sex, data = df)N Observed Expected (O-E)^2/E (O-E)^2/V
sex=1 15       13    13.43    0.0140    0.0569
sex=2  5        5     4.57    0.0412    0.0569Chisq= 0.1  on 1 degrees of freedom, p= 0.8 

2.4 可视化

fit = survfit(Surv(time,status)~sex,data = df)
library(survminer)
ggsurvplot(fit, data = df,#conf.int = TRUE,pval = TRUE,                     # logrank秩检验fun = "pct",                     # 生存率转换为百分数risk.table = TRUE,               # 添加风险表size = 1,linetype = "strata",palette = c("#E7B800","#2E9FDF"),legend = "bottom",legend.title = "Sex",legend.labs = c("Male","Female")) # 1代表Male，2代表Female

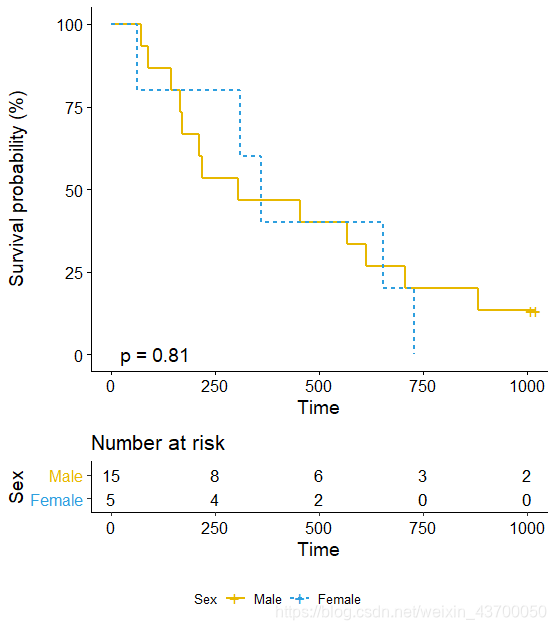
从上图可以看出男性和女性患者生存率并没有区别。

本博客内容将同步更新到个人微信公众号：生信玩家。欢迎大家关注~~~