信道估计之MMSE算法
- 前言
- MMSE估计的原理
- 总结
前言
前篇分析了LS信道估计算法,也说明了由于没有考虑SNR的影响,所以LS算法不适合在低信噪比的情况下使用。本篇来学习信道估计的另外一种常用的算法–MMSE。
为什么说LS没有考虑噪声大小的情况呢,因为LS算法使用的是实际观测量与估计观测量的误差,这并不能精确的代表估计量的真值与估计值的误差,因此在MMSE估计算法中,直接使用估计量真值与估计值的误差,作为优化的目标。这样就将噪声的影响消除掉了,因此能得到比LS估计更精确的估计值。
MMSE估计的原理
首先,依旧是给出假定的信号关系式

Y为接收数据(包含多径)大小为Nx1。
X为先验信息,大小为NXM。
h为信道冲激响应,大小为MX1。
Z为噪声,大小为NX1。
MMSE信道估计的代价函数为

h ̂mmse为MMSE准则下估计的信道冲激响应,且h ̂mmse=WY,则

分别求代价函数对W的一阶导数和二阶导数,

可见,代价函数对W的二阶导数为正定矩阵,则其一阶导数的零点对应了代价函数的最小值。这就直接得出了MMSE准则下的信道估计结果。
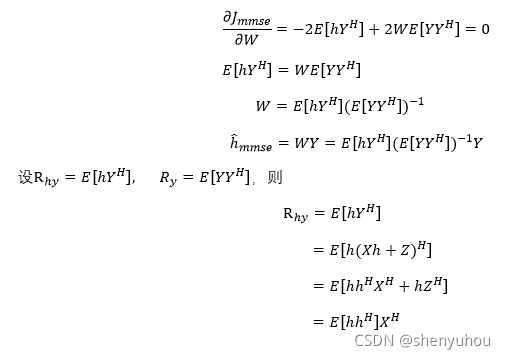

总结
通过上述公式的推导,可以看到MMSE信道估计的计算,用到了LS信道估计的结果,并且还需要知道信道相关矩阵Rh以及信道噪声的平均功率σ2,才能进行计算,计算式中有两个矩阵求逆运算,可见其计算量比较巨大,不太适合直接计算,因此又出现了LMMSE信道估计。
信道相关矩阵Rh以及信道噪声的平均功率σ2,都可通过LS估计的结果得到。具体方法就不做详述了。