CRC校验查表法原理及实现（CRC-16）

article/2025/9/27 14:27:24

绪论

在网上浏览了很多关于CRC校验的文章，基本上都是针对CRC校验原理的阐述以及关于CRC校验查表法的实际应用以及具体软件实现方法。
至于查的表是怎么来的，软件为什么要这样实现很多文章并没有说明。本篇文章就针对这两点问题进行总结和归纳，有错误的地方欢迎大家评论区指出，不胜感激。
注意：本篇文章不涉及CRC校验的基本原理，如果不了解CRC的基本原理，请移步至如下链接：
CRC查找表法推导及代码实现比较
以下的CRC查表法的软件实现及推导过程均建立在modbusRTU协议使用的CRC-16标准。

查表法的表是怎么来的？

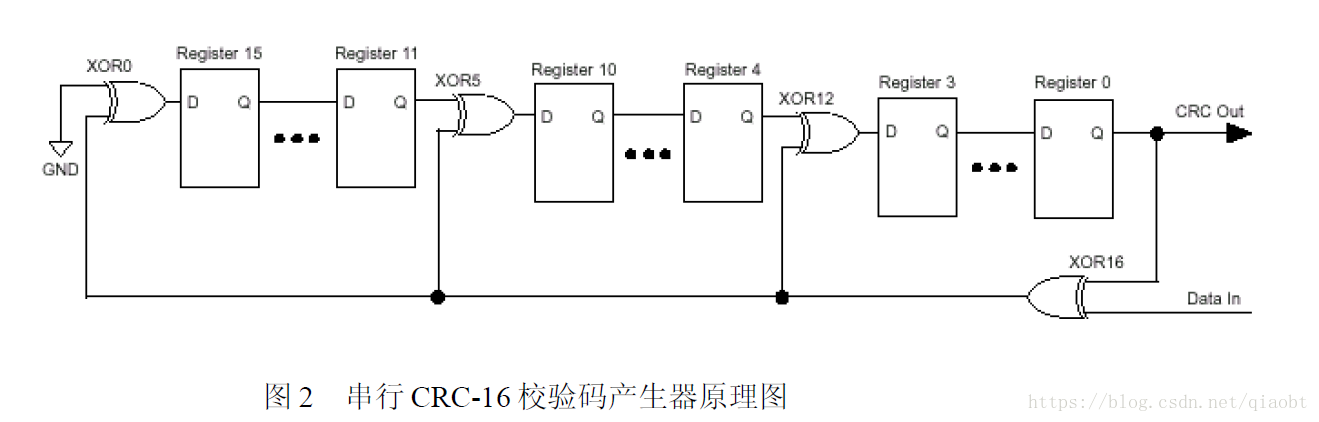
CRC16算法的生成多项式 x 16 + x 15 + x 2 + 1 x^{16}+x^{15}+x^2+1 x16+x15+x2+1，十六进制表示为0x8005。
CRC16常见的表格中的数据是按照先传输LSB，消息右移进寄存器来计算的。因此需要判断寄存器的最低位LSB，同时要将0x8005按位颠倒后(0xA001)根据LSB的情况决定是否与寄存器异或即可。
CRC16的表格中对应的数依次为0~255计算出来的CRC值，因此，此处只选取其中一两个数作为实例计算CRC值。
具体步骤如下所示：
1)从0~255中选取需要计算的数，将其对应的十六进制数放入一个长度为16的寄存器的低八位，高八位填充0；
2)如果寄存器的末位LSB为1，将寄存器的数值右移1位，再与0xA001位异或，否则仅将寄存器右移1位；
3)重复第2步，直到低八位全部右移出寄存器；
4)寄存器中的值则为校验码。
例如选择0x01作为计算CRC值：

CRC-16的表格计算
举例：0x0001
多项式：0xA001
初始值：0x0000
以下为二进制显示
00000001 高八位填充0,与初始值异或  得到：
00000000 00000001 第一次由于LSB=1 右移一位，高位添0
00000000 00000000 与0xA001异或 得到：
10100000 00000001第二次由于LSB=1 右移一位，高位添0
01010000 00000000 与0xA001异或 得到：
11110000 00000001 第三次由于LSB=1 右移一位，高位添0
01111000 00000000 与0xA001异或 得到：
11011000 00000001 第四次由于LSB=1 右移一位，高位添0
01101100 00000000 与0xA001异或 得到：
11001100 00000001 第五次由于LSB=1 右移一位，高位添0
01100110 00000000 与0xA001异或 得到：
11000110 00000001 第六次由于LSB=1 右移一位，高位添0
01100011 00000000 与0xA001异或 得到：
11000011 00000001 第七次由于LSB=1 右移一位，高位添0
01100001 10000000 与0xA001异或 得到：
11000001 10000001 第八次由于LSB=1 右移一位，高位添0
01100000 11000000 与0xA001异或 得到：
11000000 11000001 结束  得到0xC0 C1
此数值即为CRC校验值，该数值也是CRC校验表上的0x01位置上的值

我们对照一下CRC校验表，C0 C1分别为两张表中位置为1的数值（0开始），CRC校验表见“软件实现方法”部分。

当然，细心的朋友在实际应用的时候发现，如果使用CRC-16（modbus）参数模型计算CRC校验和上面的计算结果有很大差异，我们这里使用CRC校验计算器来计算校验和，链接如下：
链接: CRC在线计算
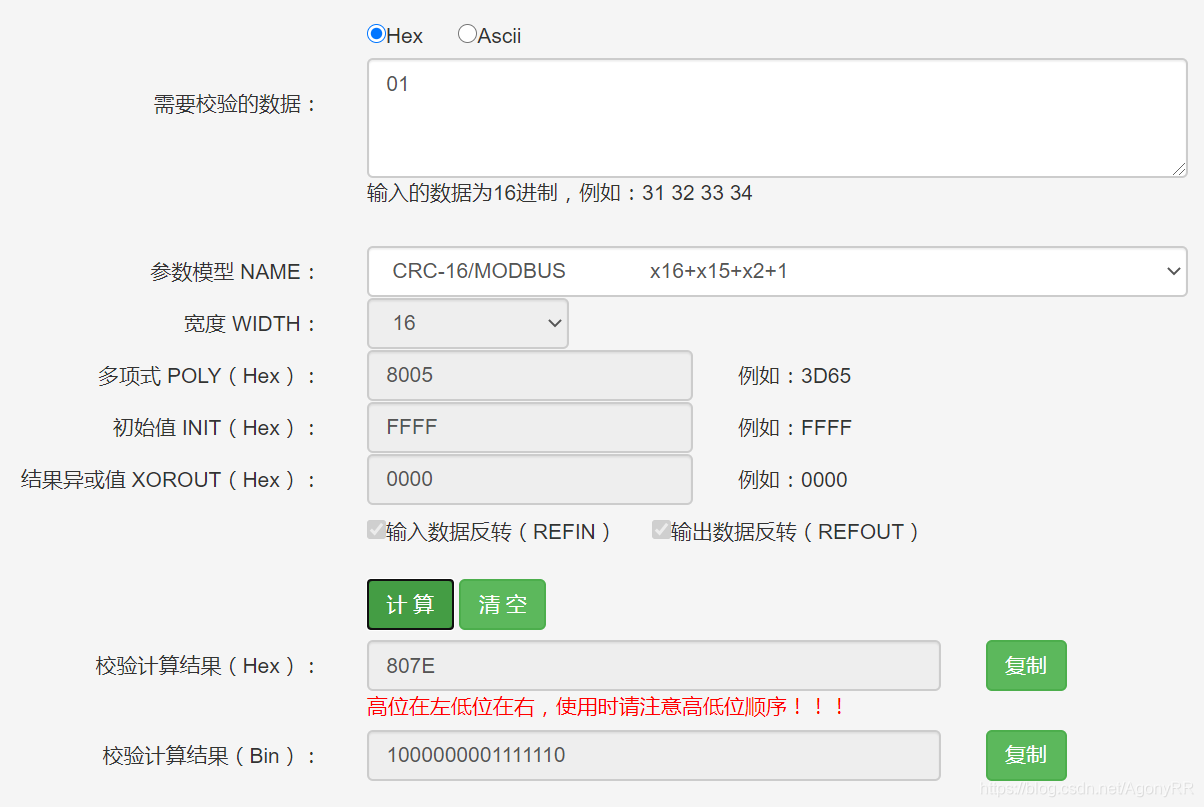
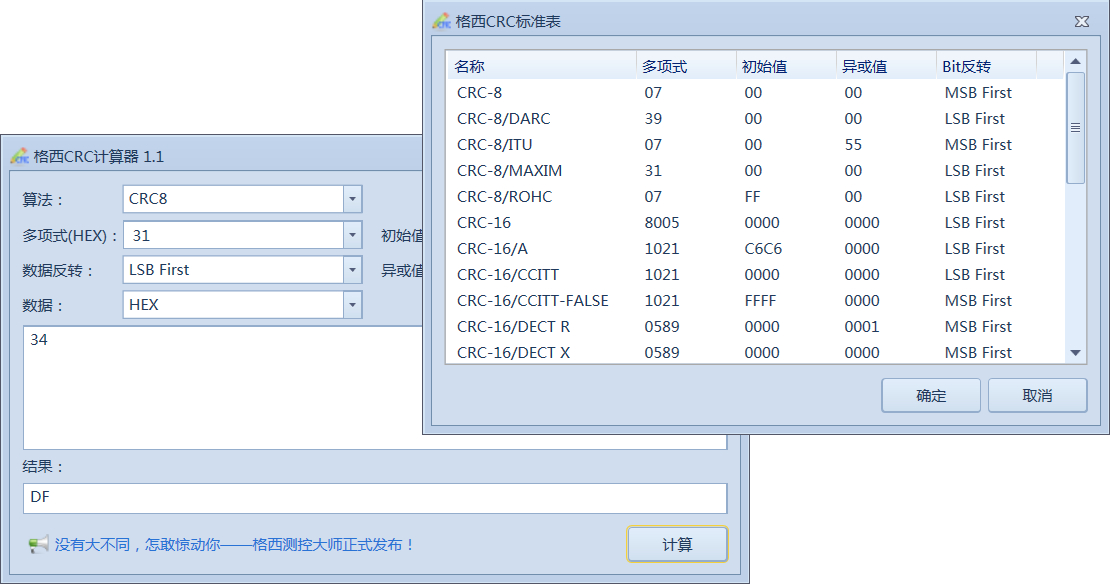
设置如截图所示：
Modbus参数模型计算CRC校验
计算结果为807E，并不是我们之前计算出来的C0C1。
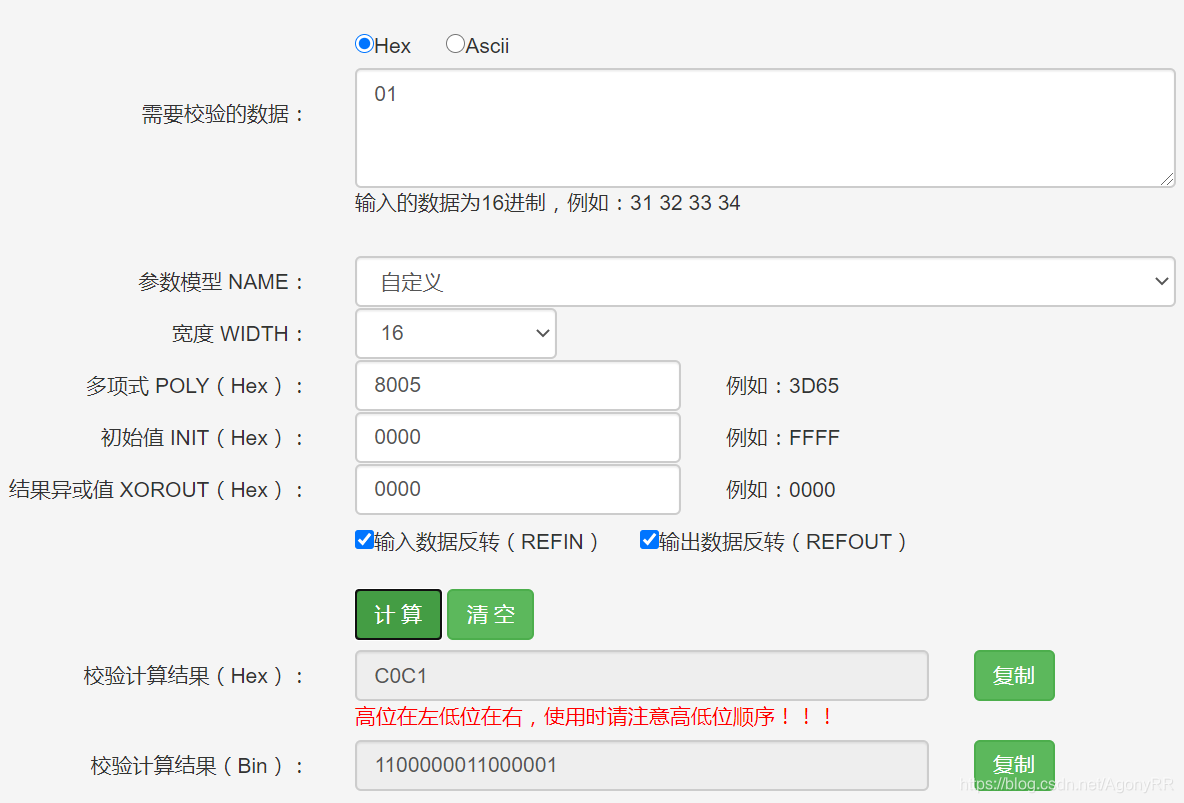
原因就在于初始值不一样，modbus参数模型要求初始值为FFFF，而CRC校验表中的数据是利用初始值0000计算得到的，如果将初始值更改为0000，其他参数不变的话，我们可以利用计算器很顺利的得到C0C1，如下截图所示：
在这里插入图片描述
modbus参数模型在计算多组数据时，上一个数据计算出来的CRC校验和是保存在CRC寄存器中，参与下一个数据的计算。
这里总结了一下使用modbus参数模型计算CRC-16的计算步骤：

1．设置CRC寄存器，并给其赋值FFFF(hex)。
2．将数据的第一个8-bit字符与16位CRC寄存器的低8位进行异或，并把结果存入CRC寄存器。
3．CRC寄存器向右移一位，MSB补零，移出并检查LSB。
4．如果LSB为0，重复第三步；若LSB为1，CRC寄存器与多项式码相异或。
5．重复第3与第4步直到8次移位全部完成。此时一个8-bit数据处理完毕。
6．重复第2至第5步直到所有数据全部处理完成。
7．最终CRC寄存器的内容即为CRC值。

软件实现方法

const uint32_t auchCRCHi[256] =
{
0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40,
0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41,
0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41,
0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40,
0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41,
0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40,
0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40,
0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41,
0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41,
0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40,
0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40,
0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41,
0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40,
0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41,
0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41,
0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40
};
const uint32_t auchCRCLo[256] =
{
0x00, 0xC0, 0xC1, 0x01, 0xC3, 0x03, 0x02, 0xC2, 0xC6, 0x06, 0x07, 0xC7, 0x05, 0xC5, 0xC4, 0x04,
0xCC, 0x0C, 0x0D, 0xCD, 0x0F, 0xCF, 0xCE, 0x0E, 0x0A, 0xCA, 0xCB, 0x0B, 0xC9, 0x09, 0x08, 0xC8,
0xD8, 0x18, 0x19, 0xD9, 0x1B, 0xDB, 0xDA, 0x1A, 0x1E, 0xDE, 0xDF, 0x1F, 0xDD, 0x1D, 0x1C, 0xDC,
0x14, 0xD4, 0xD5, 0x15, 0xD7, 0x17, 0x16, 0xD6, 0xD2, 0x12, 0x13, 0xD3, 0x11, 0xD1, 0xD0, 0x10,
0xF0, 0x30, 0x31, 0xF1, 0x33, 0xF3, 0xF2, 0x32, 0x36, 0xF6, 0xF7, 0x37, 0xF5, 0x35, 0x34, 0xF4,
0x3C, 0xFC, 0xFD, 0x3D, 0xFF, 0x3F, 0x3E, 0xFE, 0xFA, 0x3A, 0x3B, 0xFB, 0x39, 0xF9, 0xF8, 0x38,
0x28, 0xE8, 0xE9, 0x29, 0xEB, 0x2B, 0x2A, 0xEA, 0xEE, 0x2E, 0x2F, 0xEF, 0x2D, 0xED, 0xEC, 0x2C,
0xE4, 0x24, 0x25, 0xE5, 0x27, 0xE7, 0xE6, 0x26, 0x22, 0xE2, 0xE3, 0x23, 0xE1, 0x21, 0x20, 0xE0,
0xA0, 0x60, 0x61, 0xA1, 0x63, 0xA3, 0xA2, 0x62, 0x66, 0xA6, 0xA7, 0x67, 0xA5, 0x65, 0x64, 0xA4,
0x6C, 0xAC, 0xAD, 0x6D, 0xAF, 0x6F, 0x6E, 0xAE, 0xAA, 0x6A, 0x6B, 0xAB, 0x69, 0xA9, 0xA8, 0x68,
0x78, 0xB8, 0xB9, 0x79, 0xBB, 0x7B, 0x7A, 0xBA, 0xBE, 0x7E, 0x7F, 0xBF, 0x7D, 0xBD, 0xBC, 0x7C,
0xB4, 0x74, 0x75, 0xB5, 0x77, 0xB7, 0xB6, 0x76, 0x72, 0xB2, 0xB3, 0x73, 0xB1, 0x71, 0x70, 0xB0,
0x50, 0x90, 0x91, 0x51, 0x93, 0x53, 0x52, 0x92, 0x96, 0x56, 0x57, 0x97, 0x55, 0x95, 0x94, 0x54,
0x9C, 0x5C, 0x5D, 0x9D, 0x5F, 0x9F, 0x9E, 0x5E, 0x5A, 0x9A, 0x9B, 0x5B, 0x99, 0x59, 0x58, 0x98,
0x88, 0x48, 0x49, 0x89, 0x4B, 0x8B, 0x8A, 0x4A, 0x4E, 0x8E, 0x8F, 0x4F, 0x8D, 0x4D, 0x4C, 0x8C,
0x44, 0x84, 0x85, 0x45, 0x87, 0x47, 0x46, 0x86, 0x82, 0x42, 0x43, 0x83, 0x41, 0x81, 0x80, 0x40
};void crc16_str_sent(uint32_t *ptr, uint32_t len)
{WORD_BYTE  calc_crc; uint32_t uIndex;calc_crc.word=0xffff;for(; len; len--){uIndex  = calc_crc.byte.low ^ (*ptr);calc_crc.byte.low = calc_crc.byte.high ^ auchCRCHi[uIndex];calc_crc.byte.high = auchCRCLo[uIndex];ptr++;}(*ptr) = calc_crc.byte.low;ptr++;(*ptr) = calc_crc.byte.high;
}uint32_t crc16_str_rece(uint32_t *ptr, uint32_t len)
{WORD_BYTE  calc_crc; uint32_t uIndex;uint32_t dat;calc_crc.word=0xffff;for(; len; len--){uIndex  = calc_crc.byte.low ^ (*ptr);calc_crc.byte.low = calc_crc.byte.high ^ auchCRCHi[uIndex];calc_crc.byte.high = auchCRCLo[uIndex];ptr++;}if( ((*ptr)==calc_crc.byte.low) && ((*(ptr+1))==calc_crc.byte.high) )dat = 1;elsedat = 0;return(dat);
}

注意：以上代码仅仅作为参考代码，使用不同的编译器需要对代码进行简单的移植或处理即可使用。


http://chatgpt.dhexx.cn/article/iGiaKIGc.shtml

相关文章

CRC校验原理

CRC校验原理

线性分组码中有一种重要的码称为循环码（Cyclic code），这种码编码和解码都不太复杂，而且检（纠）错能力较强。循环码除了具有线性分组码的一般性质外，还具有循环性。循环性是指任一码组循环一位以后…
阅读更多...
CRC码计算及校验原理计算

CRC码计算及校验原理计算

如何根据多项式计算 循环CRC码 5.3.2 循环冗余校验检错方案 奇偶校验码（PCC）只能校验一位错误，本节所要介绍的循环冗余校验码（CRC）的检错能力更强，可以检出多位错误。 1. CRC校验原理 CRC校验原理看…
阅读更多...
CRC码计算及校验原理的最通俗诠释

CRC码计算及校验原理的最通俗诠释

在上一篇发布了我的最新著作《深入理解计算机网络》一书的原始目录（http://blog.csdn.net/lycb_gz/article/details/8199839），得到了许多读者朋友的高度关注和肯定，本篇接着发一篇关于CRC码校验原理和CRC码计算方面的通俗诠释的试…
阅读更多...
最好懂的CRC校验规则讲解

最好懂的CRC校验规则讲解

文章目录 前言何为校验如何生成CRC校验码按字节位反转确定左移多少位生成多项式的数值式模二除法其它说明 前言 CRC校验的原理非常复杂，但是用起来却很简单，甚至别人写好了函数，直接拿来调用即可，但是我们还是需要了解一点这个校…
阅读更多...
CRC校验原理及代码

CRC校验原理及代码

参考：CRC校验原理及步骤https://blog.csdn.net/d_leo/article/details/73572373 什么是CRC校验？ CRC即循环冗余校验码：是数据通信领域中最常用的一种查错校验码，其特征是信息字段和校验字段的长度可以任意选定。循环冗余检查&am…
阅读更多...
CRC 校验计算

CRC 校验计算

一、简介 CRC即循环冗余校验码（Cyclic Redundancy Check）：是数据通信领域中最常用的一种查错校验码，其特征是信息字段和校验字段的长度可以任意选定。 其根本思想就是先在要发送的帧后面附加校验码，再发送给接收端。…
阅读更多...
如何进行CRC校验

如何进行CRC校验

为了保证数据传输的可靠性，计算机网络传输数据时，必须采用差错检验措施，数据链路层广泛应用了循环冗余检验CRC（Cyclic Redundancy Check）的检错技术。 基本原理： CRC检验原理实际上就是在一个p位二进制数…
阅读更多...
CRC校验（个人小结）

CRC校验（个人小结）

前言 之前曾经在通信原理课程学习过、也在项目中使用软件模拟过CRC校验。但是仍然有许多困惑的地方，在网上找的资料也是零零散散，于是自己根据课程学习、项目实践以及网上的资料，做一个小结。不当之处请在评论区指出。推荐一个CRC在线校验工…
阅读更多...
CRC码校验纠错原理

CRC码校验纠错原理

在接收端收到了CRC码后用生成多项式为G(x)去做模2除，若得到余数为0,则码字无误。若如果有一位出错，则余数不为0，而且不同位出错，其余数也不同。可以证明，余数与出错位的对应关系只与码制及生成多项式有关，而…
阅读更多...
CRC校验详解（附代码示例）

CRC校验详解（附代码示例）

目录 1.CRC校验原理 2.生成多项式 3.以CRC-16校验为例讲解编程实现 3.3.1 完全按照CRC原理实现校验 3.3.2 工程中常用CRC校验过程 3.3.3 改进的CRC校验过程 4.以CRC-8校验为例讲解查表法 5.以CRC-16校验为例讲解查表法 5.1.生成表格 5.2.查表法实现 6.代码链接 CRC校…
阅读更多...
详述CRC校验码（附代码）

详述CRC校验码（附代码）

关注星标公众号，不错过精彩内容 来源 | 一口Linux CRC校验应用比较广泛，通常在通信领域用的比较多，即便是自定义通信协议，也可以添加CRC校验码，使其通信更加可靠。 今天就来进一步描述CRC校验码。 一、CRC概念 1. 什么…
阅读更多...
【科普】CRC校验（一）什么是CRC校验？

【科普】CRC校验（一）什么是CRC校验？

目录 CRC（循环冗余校验） CRC 校验码的生成 CRC 的发送方与接收方 发送方 接收方 除法异或运算示意图 CRC（循环冗余校验） CRC（Cyclic Redundancy Check）循环冗余检验，是一种用于检测数字数…
阅读更多...
CRC校验原理及其C语言实现

CRC校验原理及其C语言实现

文章目录 目录前言CRC算法简介CRC参数模型CRC计算CRC校验CRC计算的C语言实现CRC计算工具总结参考资料 目录 前言CRC算法简介CRC计算CRC校验CRC计算的C语言实现CRC计算工具总结 前言 最近的工作中，要实现对通信数据的CRC计算，所以花了两天的时间好好研…
阅读更多...
Oracle Toad 导数,麒峰

Oracle Toad 导数,麒峰

标签： 补丁下载 x86 ia64 操作系统 迅雷下载 oracle it (2011-05-26 10:28) 标签： 授予的权限 主键约束 对象 角色管理 数据字典 oracle it 系统权限： create table :create any table: drop table: create procedure: execute anycedure: cr…
阅读更多...
最优捕捞

最优捕捞

一、问题重述 为了保护人类赖以生存的自然环境，可再生资源（如渔业、林业资源）的开发必须适度。一种合理、简化的策略是，在实现可持续收获的前提下，追求最大产量或最佳效益。 假设这种鱼分4个年龄组：称1龄…
阅读更多...
短期趋势自用经传捕捞季节 通达信指标公式副图 源码 贴图

短期趋势自用经传捕捞季节 通达信指标公式副图 源码 贴图

指标公式描述 短期趋势自用经传捕捞季节 通达信指标公式副图 源码 贴图 图示: 指标源码： WY1001:(2*CLOSEHIGHLOW)/4; WY1002:EMA(WY1001,2); WY1003:EMA(WY1002,2); WY1004:EMA(WY1003,2); XYS0:(WY1004-REF(WY1004,1))/REF(WY1004,1)*100; STICKLINE(XYS0>0,X…
阅读更多...
股票指标使用 - 捕捞季节

股票指标使用 - 捕捞季节

股票指标里面我觉得这个指标是最实用的了，XX软件里面流行起来的。作为IT男，任何带有逻辑运算的都会让我感兴趣。 接下来就用简单易懂的文字介绍下这个指标怎么看(百度上搜到的都说了那么深奥) 如图： 优势：相对MACD指标来说&…
阅读更多...
捕捞季节 通达信副图指标公式 源码

捕捞季节 通达信副图指标公式 源码

捕捞季节是一个趋势型指标，主要用于（超）短线的股价运行趋势状态监控。捕捞季节通达信指标公式主要用途是用来做短期买卖点操作的指标公式，适合那些做短期买卖的股民。 【指标用法】 紫色线上穿黄色线为金叉买入信号，…
阅读更多...
通达信指标：捕捞季节

通达信指标：捕捞季节

通达信【捕捞季节】指标 WY1001:(2CLOSEHIGHLOW)/3; WY1002:EMA(WY1001,3); WY1003:EMA(WY1002,3); WY1004:EMA(WY1003,3); XYS0:(WY1004-REF(WY1004,1))/REF(WY1004,1)100; STICKLINE(XYS0>0,XYS0,0,2,0),COLORRED; STICKLINE(XYS0<0,XYS0,0,2,0),COLORGREEN; PJGJ:AMO…
阅读更多...
x86服务器与arm服务器

x86服务器与arm服务器

服务器是提供计算服务的设备&#xff0c;服务器的构成包括处理器、硬盘、内存、系统总线等&#xff0c;和通用的计算机架构类似&#xff0c;但是由于需要提供高可靠的服务&#xff0c;因此在处理能力、稳定性、可靠性、安全性、可扩展性、可管理性等方面要求较高。在网络环境下…
阅读更多...
推荐文章

Copyright @ 2022~2023