文章目录
- 前言
- 一、Huffman编码是什么?
- 二、Huffman编码的实现方法
- 三、Huffman压缩文件
- 1.统计文件个字符出现的次数
- 2.生成Huffman树
- 3.生成码表
- 4.对文件进行压缩
- 四、Huffman解压文件
- 五、实验结果
- 总结
前言
这个实验是我在学习信息论与编码时所做的课程实验,是用来学习Huffman编码的。整个项目是使用c++在VS2022下编写完成的。工程文件我已经发送我的仓库中,有需要的小伙伴可以通过文章最下面的链接自取。
一、Huffman编码是什么?
Huffman编码是一种无失真的信源编码方式。它通过根据字符出现的概率来分配长码与短码,从而达到降低平均码长的目的,实现压缩效果。
二、Huffman编码的实现方法
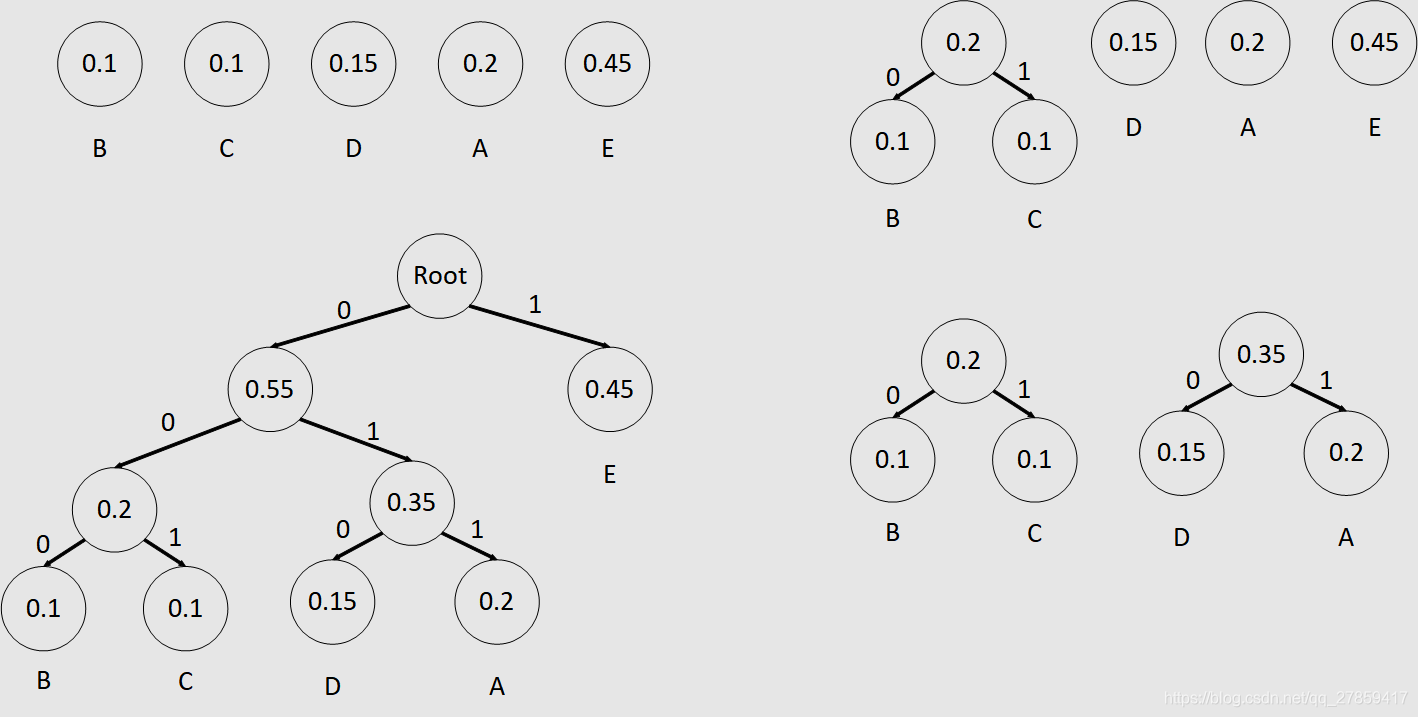
Huffman编码的具体实现方法是采用自底向上构造二叉树的方法,就是对所有信源符号按概率从高到低进行排序,每次合并概率最低的两个符号的概率,作为一个新的符号的概率,然后对所有的符号概率再重新排序合并概率最低的两个符号,这一过程一直持续,直到最后概率合并为1.
三、Huffman压缩文件
压缩文件由Encoder类进行实现,Encoder类的定义如下:
#pragma once
#ifndef ENCODER_H
#define ENCODER_H#include"huffmantree.h"
#include<vector>
#include<fstream>
#include<iostream>
#include <algorithm>
using namespace std;class Encoder
{
private :const int size = 256;vector<int> counter;ifstream input;ofstream output;vector<HuffmanTree*> leaf;vector<vector<unsigned char>> p; // 码表HuffmanTree* tree_head;int file_size;bool openFile(string source_file, string target_file);void statistics();// 统计各个字符出现次数,并进行排序void createTree();// 生成huffman树void destroyTree(HuffmanTree* root);void creatTable(HuffmanTree* node, vector<char> temp, int len);public:Encoder();void compress(string source_file, string target_file); // 压缩编码~Encoder();};#endif
HuffmanTree的定义如下
#pragma once
#ifndef HUFFMANTREE_H
#define HUFFMANTREE_Hstruct HuffmanTree
{HuffmanTree* lchild;HuffmanTree* rchild;int weight; //出现次数unsigned char data;unsigned char code; // 左1右0
};#endif
下面我将重点说明一下statistics()、createTree()、creatTable()、和 compress()
1.统计文件个字符出现的次数
void Encoder::statistics()
{unsigned char buff;while (input >> noskipws >> buff){counter.at(buff)++;file_size++;}cout << "the size of file is " << file_size << " byte"<<endl;input.clear();input.seekg(0, ios::beg); //将文件指针指向开头
}
这里的文件需要用二进制打开,否则在Windows下会出现文档中0X1A被认作为EOF的情况,使得读取文件异常终止。
2.生成Huffman树
代码如下:
void Encoder::createTree()
{ for (int i = 0; i < size; ++i){leaf.at(i) = new HuffmanTree;leaf.at(i)->weight = counter.at(i);leaf.at(i)->code = i;leaf.at(i)->data = i;leaf.at(i)->lchild = NULL;leaf.at(i)->rchild = NULL;} //初始化HuffmanTree* lnode;HuffmanTree* rnode;HuffmanTree *f;//f = new HuffmanTree[size];while (leaf.size() > 1){f = new HuffmanTree;//从大到小排序,每次取最后两个sort(leaf.begin(), leaf.end(), [=](HuffmanTree* i1, HuffmanTree* i2) {return i1->weight > i2->weight;}); lnode = leaf.back();leaf.pop_back();rnode = leaf.back();leaf.pop_back();f->lchild = lnode;lnode->code = 1; //左1右0f->rchild = rnode;rnode->code = 0;f->weight = rnode->weight + lnode->weight;f->code = 0;leaf.push_back(f);if (leaf.size() == 1){tree_head = f;leaf.pop_back();return;}f++;}return ;
}
对所有信源符号按概率从高到低进行排序,每次合并概率最低的两个符号的概率,作为一个新的符号的概率,然后对所有的符号概率再重新排序合并概率最低的两个符号
3.生成码表
void Encoder::creatTable(HuffmanTree* node, vector<char> temp, int len)
{ if (node != NULL){if (node->lchild == NULL && node->rchild == NULL) {temp.at(len) = node->code;p.at(node->data).assign(temp.begin()+1, temp.begin()+len+1);//用来存放码表}else{temp.at(len++) = node->code;creatTable(node->lchild, temp, len);creatTable(node->rchild, temp, len);}}
}
利用递归遍历二叉树来生成码表
4.对文件进行压缩
void Encoder::compress(string source_file, string target_file)
{vector<char> temp(size, 0);unsigned char buff; //存放读入的字符unsigned char out = 0; //输出的字符vector<char> code; //存放字符的编码openFile(source_file, target_file); //打开输入输出文件,必须要用二进制打开statistics(); //统计各个字符出现次数createTree();//生成Huffman树creatTable(tree_head, temp, 0);//构造码表for (vector<int>::iterator it = counter.begin(); it != counter.end(); ++it){output << *it << endl;}//写入每个字符出现的次数,解压时根据这个构建Huffman树while (input >> noskipws >> buff){code.insert(code.end(), p[buff].begin(), p[buff].end());while (code.size() >= 8) //当编码中0和1位数超过8时,将他们转化成一个字符输出{out = 0;for (int j = 0; j < 8; ++j){out = out ^ (code.at(j) << j);}output << out;vector<char>::const_iterator First = code.begin() + 8; vector<char>::const_iterator Second = code.end();code.assign(First, Second); //将输出的编码删除}}if (code.size() != 0) //多出来不足八位的编码进行补零操作{for (int j = 0; j < code.size(); ++j){out = out ^ (code.at(j) << j);}output << out;output << code.size(); //这个记录的是最后字符的长度,解压其实并没有用到这个信息,可以删除}output.close();input.close();
}
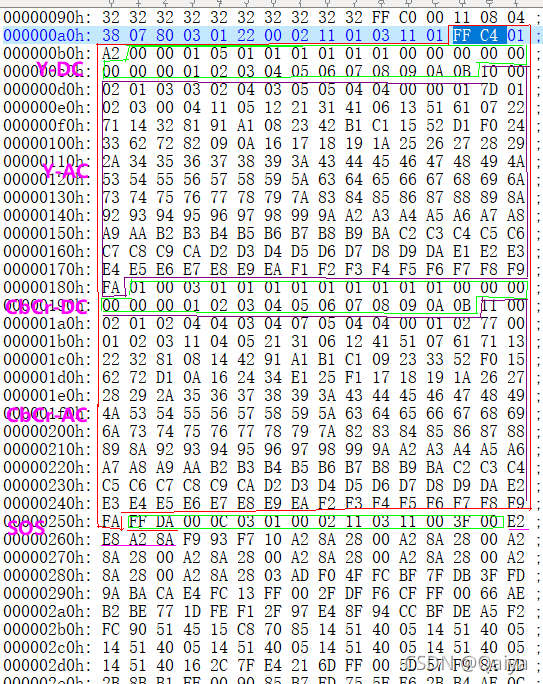
压缩时一定要将码表先写入到压缩文件中,否者无法对文件进行解压缩,同时写入字符对应的编码时,编码中的0和1是要当作位信息写入的,我这里将编码后的0和1每八个为一组当成一个字节写入到文件中去的,最后不足8位的进行补零。
四、Huffman解压文件
void Decoder::deCompress(string sourece_file,string target_file) // 解压
{HuffmanTree* p;unsigned char buff;int count = 0;int temp;openFile(sourece_file, target_file);statistics();createTree();p = root;for (vector<int>::iterator it = counter.begin(); it != counter.end(); ++it){file_size += *it;}input >> noskipws >> buff;while (input >> noskipws >> buff){for (int i = 0; i < 8; ++i){if (!(p->lchild == NULL && p->rchild == NULL)){temp = (buff & (1 << i)) ? 1 : 0;//cout << temp;if (temp == 0){p = p->rchild;}elsep = p->lchild;}else{output << p->data;p = root;count++;if (count == file_size){cout << "decompress successfully";return;}} }}input.close();output.close();
}
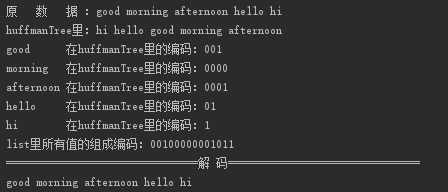
解压文件的代码大部分和压缩文件时的一样,这里比较重要的代码如上所示。主要是以二进制形式读取压缩文件中的每一个字符,并且将每一个字符按位拆分为01序列。从树的根开始,0寻找右子树,1寻找左子树,直到找到一个叶子节点,说明译码成功。将指针重新指向根节点重复该过程即可完成解压。
五、实验结果
#include"decoder.h"
#include"encoder.h"
//#include"vld.h"
int main()
{Encoder en;Decoder de;string source =R"(.\img\2.bmp)"; //目标文件string temp = R"(.\output\2.bin)"; //压缩后文件string target = R"(.\output\2.bmp)"; //解压后文件en.compress(source, temp);de.deCompress(temp, target);return 1;
}
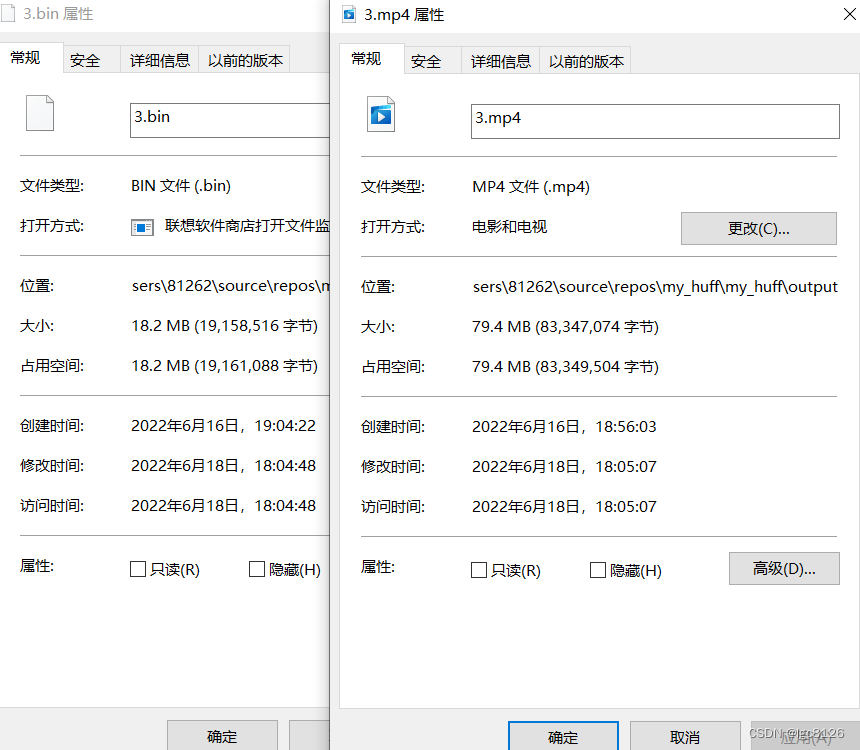
该程序使用二进制读取文件,理论上来说任何格式的文件都可以进行压缩。如上图,对一个80M的mp4文件进行压缩,压缩出的文件只有18M,但是整个程序的运行时间大约需要三分钟!
总结
这次实验涉及的内容十分广泛:对文件的读取、排序算法、二叉树等等。
我将整个项目放在了我的仓库中,有需要的伙伴可以自取。
Huffman编码对不同的文件压缩效率也不一样,可以更换不同的文件试一试它的压缩效率。
https://github.com/logic8126/huffman-coding