Huffman Tree

哈夫曼树；哈夫曼编码；最优二叉树
自底向上
变长编码；前缀编码；熵编码
数据无损压缩；最短编码；最佳判定树

一、基本概念

1. Huffman Tree，又称最优二叉树，是带权路径长度最短的树，权值较大的结点离根较近。
   定义：给定n权值作为n个叶子节点，构造一棵二叉树，若这棵二叉树的带权路径长度达到最小，则称这样的二叉树为最优二叉树，也称为Huffman树。

2. 路径：在一棵树中，从一个结点往下可以达到的孩子或孙子结点之间的通路。

3. 路径长度：通路中分支的数目称为路径长度。
   e.g. 若规定根结点的层数为$1$，则从根结点到第$L$层结点的路径长度为$L-1$。

4. 结点的权：若将树中结点赋给一个有着某种含义的数值，则这个数值称为该结点的权。

5. 带权路径长度：从根结点到该结点之间的路径长度与该结点的权的乘积。

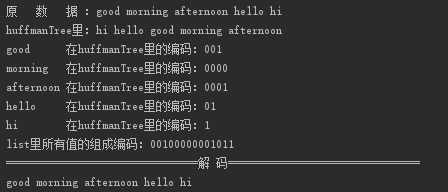
6. 树的带权路径长度：树的带权路径长度规定为所有叶子结点的带权路径长度之和，记为WPL
   $$WPL=\sum _{i=1}^n{w}_i{l}_i$$
   其中，$n$表示叶子结点的数目，$w_i$和$l_i$分别表示叶子结点$k_i$的权值和树根结点到叶子结点$k_i$之间的路径长度。

二、性质

1. 不唯一（具有相同带权结点）；左右子树可以互换；
2. 带权值的节点都是叶子节点；
3. Huffman tree中只有叶子节点和度为$2$的节点，没有度为1的节点；
4. 一棵有$n$个叶子节点的Huffman tree共有$2n-1$个节点，需要$n-1$次合并。

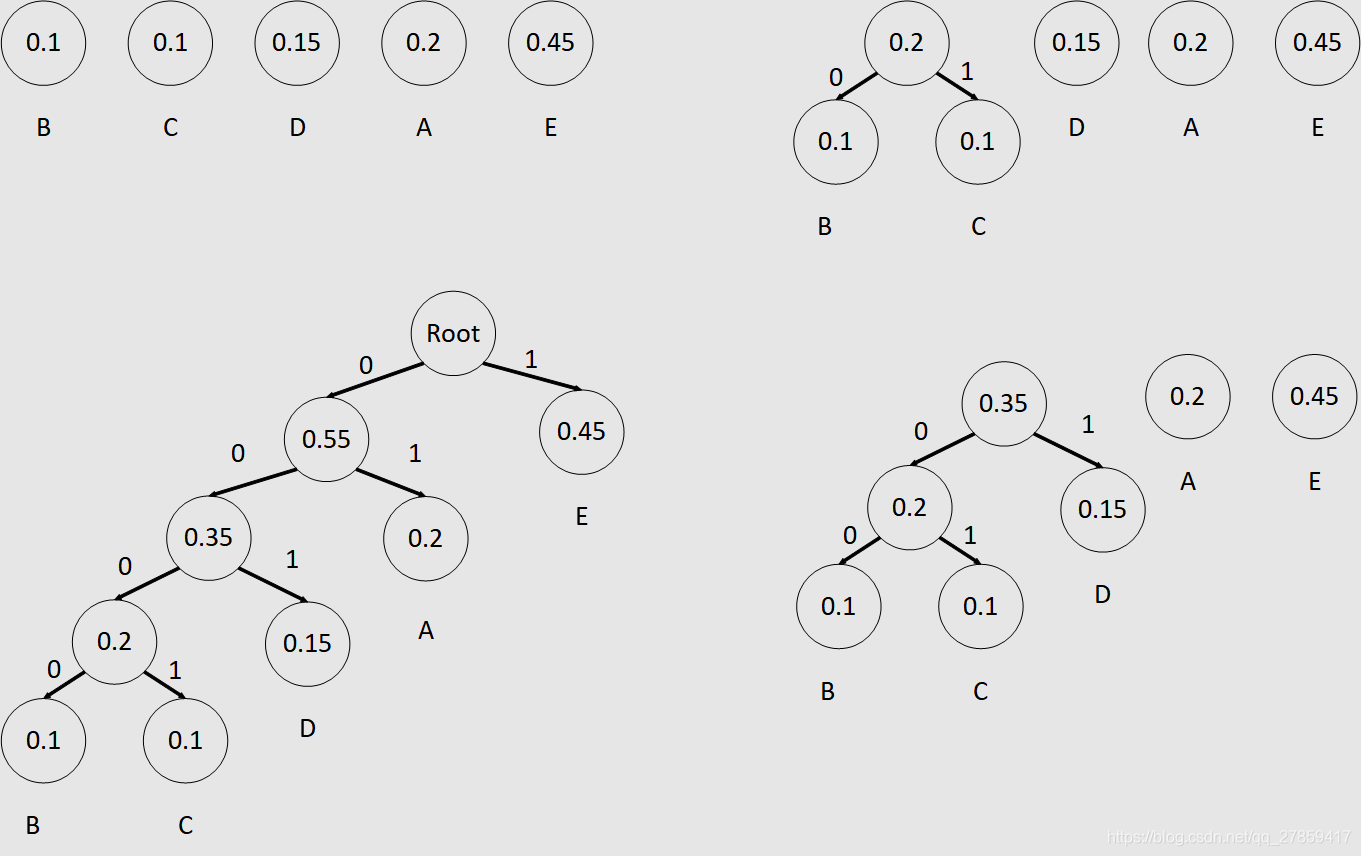
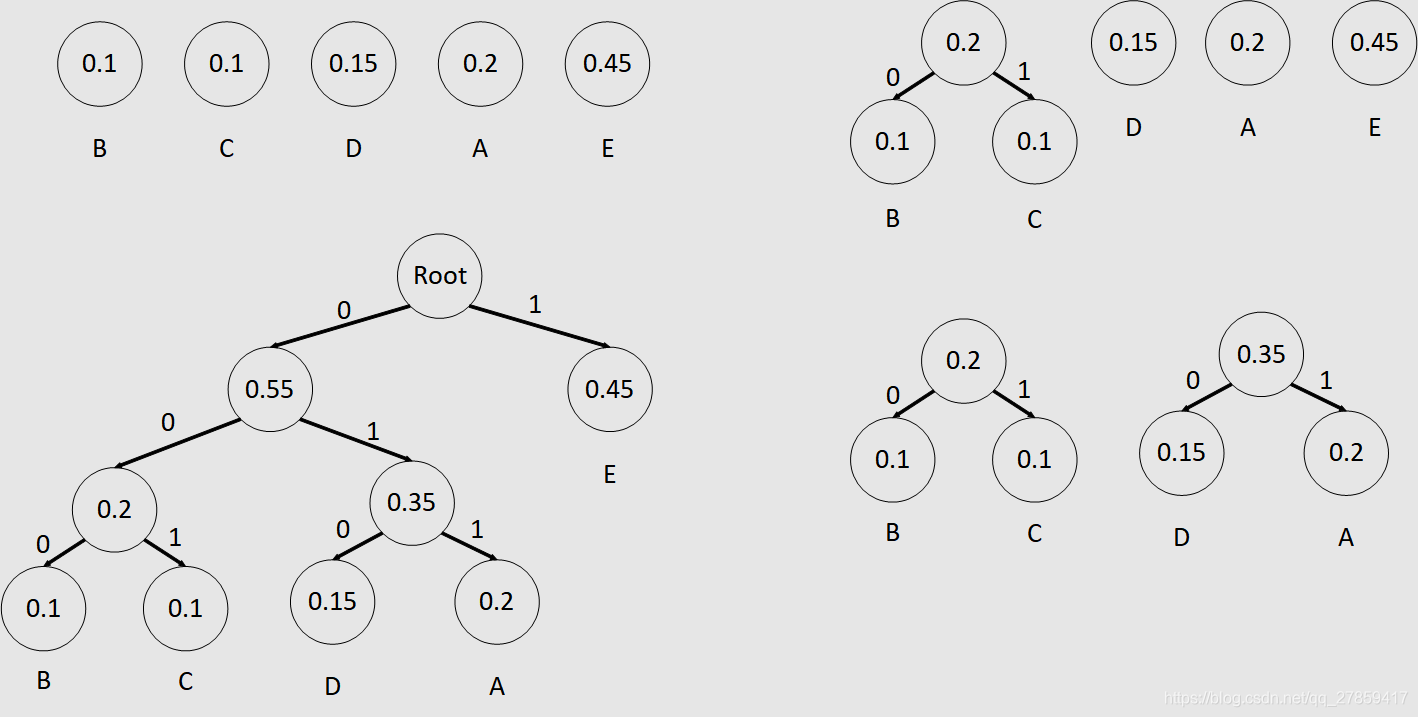
三、构造

假设有$n$个权值，则构造出的哈夫曼树有$n$个叶子结点。 $n$个结点的权值分别设为$w_1,w_2,\dots ,w_n$，则哈夫曼树的构造规则为：

1. 将$w_1,w_2,\dots ,w_n$看成是有$n$棵树的森林(每棵树仅有一个结点)；
2. 在森林中选出两个根结点的权值最小的树合并，作为一棵新树的左、右子树，且新树的根结点权值为其左、右子树根结点权值之和；
3. 从森林中删除选取的两棵树，并将新树加入森林；
4. 重复(2)、(3)步，直到森林中只剩一棵树为止，该树即为所求得的哈夫曼树。
   
   

四、应用—— Huffman Coding

1. 定义：Huffman Coding是一种用于无损数据压缩的熵编码（权编码）算法。由美国计算机科学家大卫·霍夫曼（David Albert Huffman）在1952年发明。
2. 性质：
   • 变长码：频繁出现的字符分配更短的码；不频繁出现的字符分配更长的码
   • 前缀编码（立刻可解码性）：任一字符的编码都不会是另一字符的（更长）编码的前缀
3. 分类：
   • 静态编码：1）依据数据构建Huffman tree；2）依据Huffman tree为字符分配相应的码
     • 需要存储Huffman tree，方可解码
   • 动态编码：$t+1$个字符的编码依据前$t$个字符
     • 无需存储Huffman tree，即可解码
4. 约定：
   • 将权值小的最为左节点，权值大的作为右节点
   • 左孩子编码为0，右孩子编码为1

五、实现

1. 基于python的实现

1. 构建Huffman tree的节点对象（名称；权值；左子节点；右子节点）
2. 根据构建的Huffman tree，并生成对应的码本
   • 初始化节点对象
   • 利用heapq构建最小堆
   • 每次取出堆中最小的两个值，构成新树，循环该过程，知道仅剩一个根节点
   • 迭代编码
     • 终止条件：到达叶子节点（判断Huffman tree是否只有一个节点的特殊情况）
     • 编码左节点（0）、右节点（1）
3. 依据码本进行编码
4. 依据码本进行解码

class HeapNode(object):left = Noneright = Noneitem = Noneweight = 0def __init__(self, i, w):self.item = iself.weight = wdef setChildren(self, ln, rn):self.left = lnself.right = rndef __repr__(self):return "%s - %s — %s _ %s" % (self.item, self.weight, self.left, self.right)def __lt__(self, other):return self.weight < other.weight

from itertools import groupby
from heapq import *class HuffmanTree():def __init__(self):self.codes = {}self.reverse_mapping = {}def build_huffman_tree(self, text):itemqueue =  [HeapNode(a,len(list(b))) for a,b in groupby(sorted(text))]heapify(itemqueue)while len(itemqueue) > 1:l = heappop(itemqueue)r = heappop(itemqueue)n = HeapNode(None, r.weight+l.weight)n.setChildren(l,r)heappush(itemqueue, n)return itemqueuedef make_codes(self, s, node):if node.item:if not s:self.codes[node.item] = "0"else:self.codes[node.item] = sself.reverse_mapping[s] = node.itemelse:self.make_codes(s+"0", node.left)self.make_codes(s+"1", node.right)def encoded_text(self, text):encoded_text = ""for character in text:encoded_text += self.codes[character]return encoded_textdef decode_text(self, encoded_text):current_code = ""decoded_text = ""for bit in encoded_text:current_code += bitif(current_code in self.reverse_mapping):character = self.reverse_mapping[current_code]decoded_text += charactercurrent_code = ""return decoded_text

if __name__ == '__main__':InputFile = "./sample.txt"with open(InputFile,'r') as f:text = f.read().rstrip()huff = HuffmanTree()huffTree = huff.build_huffman_tree(text)huff.make_codes('', huffTree[0])encode = huff.encoded_text("hello")text_ = huff.decode_text(encode)print (encode)print (text_)

1010000110110101101000
hello