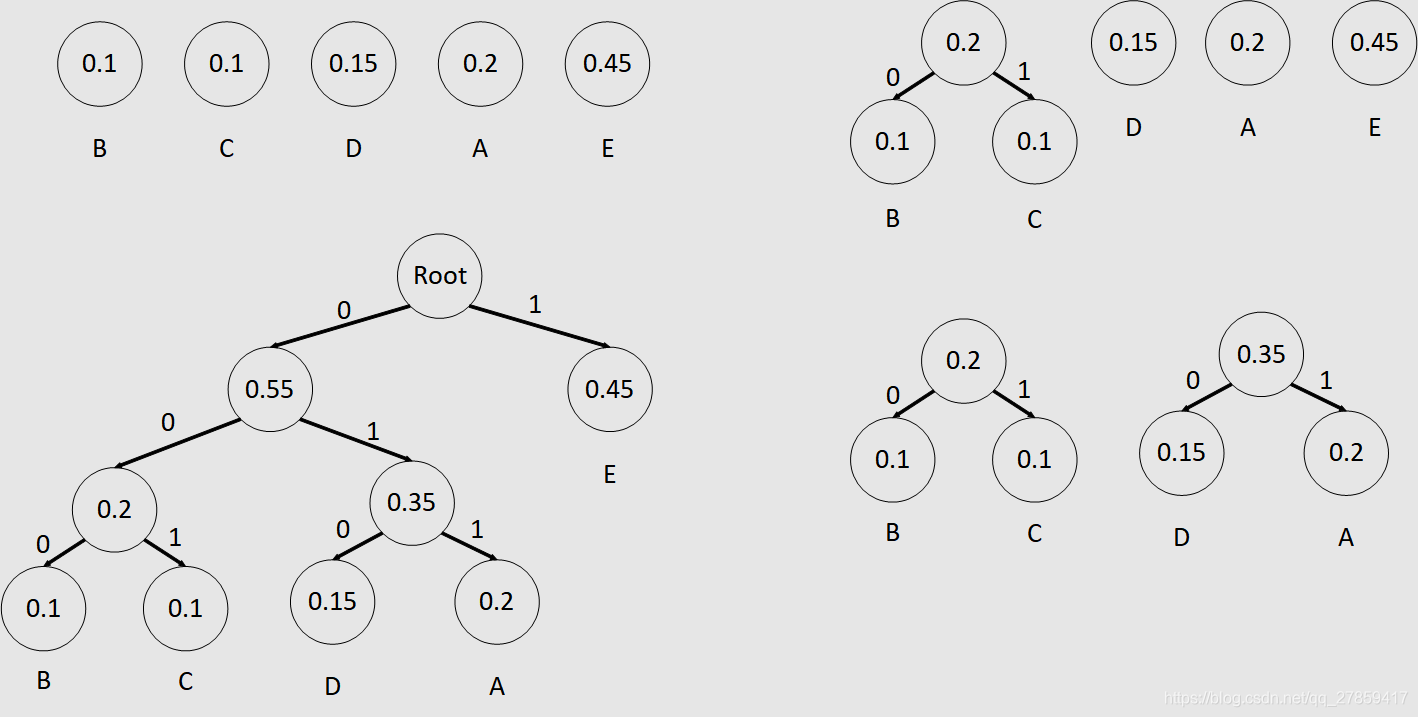
自适应Huffman编码

article/2025/9/29 1:17:14

自适应Huffman编码，可用初始编码表（数字音视频技术，实验二）

如果你已经理解了 自适应Huffman编码 ，那么你不应该浪费时间在无聊的实验上

实验目的

1、深入掌握自适应Huffman编码的原理
2、掌握自适应Huffman编码算法的实现过程
3、掌握和熟悉利用编程语言实现自适应Huffman编码器和解码器

实验要求

1、实现编码器，对输入字符给出相应的编码结果；
2、实现解码器，对步骤1中的编码结果进行解码；
3、请使用初始编码表如下：
在这里插入图片描述
4、对字符串ABBCADAD进行编码；
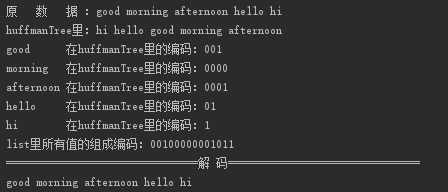
5、截图显示编码中间结果，并保证最终解码结果正确；
6、编辑程序说明文档。

实验步骤

附实验代码及说明文档

实验体会

记录实验过程中碰到的问题及解决方法、最终实验结果。

实现代码：

cpp文件，main函数里包含初始编码表 代码片.

#include "huffmanTree.h"
#include <map>
map<char, string> initCode;BinaryTree::BinaryTree(int num, int weight)
{p_root = new Node(nullptr, nullptr, nullptr);p_root->num = num; //节点的序号p_root->weight = weight;  //节点的权重值
}BinaryTree::~BinaryTree()
{deleteNode(p_root);
}bool BinaryTree::swap(Node * p_nodeA, Node * p_nodeB)
{if (p_nodeA == nullptr || p_nodeB == nullptr || p_nodeA == p_nodeB)return false;Node *pTemp;if (getBrotherState(p_nodeA) == LeftChild) { //如果A节点是左孩子if (getBrotherState(p_nodeB) == LeftChild) { // 如果B节点是左孩子pTemp = p_nodeA->p_parent->p_left;p_nodeA->p_parent->p_left = p_nodeB->p_parent->p_left;p_nodeB->p_parent->p_left = pTemp;}else {pTemp = p_nodeA->p_parent->p_left;p_nodeA->p_parent->p_left = p_nodeB->p_parent->p_right;p_nodeB->p_parent->p_right = pTemp;}}else {if (getBrotherState(p_nodeB) == LeftChild) {pTemp = p_nodeA->p_parent->p_right;p_nodeA->p_parent->p_right = p_nodeB->p_parent->p_left;p_nodeB->p_parent->p_left = pTemp;}else {pTemp = p_nodeA->p_parent->p_right;p_nodeA->p_parent->p_right = p_nodeB->p_parent->p_right;p_nodeB->p_parent->p_right = pTemp;}}pTemp = p_nodeA->p_parent;p_nodeA->p_parent = p_nodeB->p_parent;p_nodeB->p_parent = pTemp;return true;}bool BinaryTree::addNode(Node * p_parent, Node * p_child, Brother brotherState)
{if (p_parent == nullptr || p_child == nullptr)return false;if (brotherState == LeftChild) { if (p_parent->p_left != nullptr) {std::cout << "error:left child exist!" << std::endl;return false;//如果父节点有左孩子，则不能添加到左孩子位置}p_parent->p_left = p_child;//否则可以添加}else if (brotherState == RightChild) { if (p_parent->p_right != nullptr) {std::cout << "error:right child exist!" << std::endl;return false;//如果父节点有右孩子，则不能添加到右孩子位置}p_parent->p_right = p_child;//否则可以添加}else {std::cout << "error:brotherState is wrong!" << std::endl;//读取位置信息错误return false;}p_child->p_parent = p_parent;return true;
}bool BinaryTree::isAncestor(Node * p_nodeChild, Node * p_nodeAncestor)
{while (p_nodeChild != p_root) {if (p_nodeChild == p_nodeAncestor) {return true;}else {p_nodeChild = p_nodeChild->p_parent;}}return false;
}void BinaryTree::deleteNode(Node *p_node)
{if (p_node->p_left != nullptr) {deleteNode(p_node->p_left);}if (p_node->p_right != nullptr) {deleteNode(p_node->p_right);}delete p_node;
}BinaryTree::Brother BinaryTree::getBrotherState(Node *p_node)
{if (p_node->p_parent->p_left == p_node) {return LeftChild;}else {return RightChild;}
}HuffmanTree::HuffmanTree() :tree(0, 0)
{sum = 1;
}string HuffmanTree::getHuffmanCode(Node *p_n)
{std::string huffmanCode = "";std::stack<Node *> stack;std::deque<char> code;if (p_n == tree.getRoot())return "0";while (p_n != tree.getRoot()) {if (tree.getBrotherState(p_n) == tree.LeftChild) {code.push_back('0');}else {code.push_back('1');}p_n = p_n->p_parent;}while (!code.empty()) {huffmanCode += code.back();code.pop_back();}return huffmanCode;
}Node * HuffmanTree::findLarge(Node *p_node)
{std::stack<Node *> stack;Node *p = tree.getRoot();Node *large = p;while (p || !stack.empty()) {if (p != nullptr) {stack.push(p);if (p->weight == p_node->weight) {//如果large不在同权重下，则置large为pif (large->weight != p->weight) {large = p;}//同权重下的large比p小，则置large为pelse if (large->num > p->num) {large = p;}}p = p->p_left;}else {p = stack.top();stack.pop();p = p->p_right;}}if (large == tree.getRoot()) {return p_node;}return large;
}void HuffmanTree::encode( string input)
{char cbuffer;Node *nyt = tree.getRoot();bool exist = false;for (int i = 0; i < input.length(); i++) { cbuffer = input[i];		exist = false;string code;auto existNode = buffers.begin();	for (existNode; existNode != buffers.end(); existNode++) {if (existNode->key == cbuffer) {code = existNode->value;exist = true;cout << cbuffer << " 在树中存在，编码为： " << existNode->value << endl; break;}}if (exist) { Node *root = existNode->p;weightAdd(root);}else {Node *c = new Node(nullptr, nullptr, nyt);c->num = sum++;c->weight = 1;Node *NYT = new Node(nullptr, nullptr, nyt);NYT->num = sum++;NYT->weight = 0;cout << "\n NYT:" << getHuffmanCode(nyt) << endl;tree.addNode(nyt, NYT, BinaryTree::LeftChild);tree.addNode(nyt, c, BinaryTree::RightChild);nyt->weight = 1;cout << cbuffer << "首次出现，编码为："<< initCode.at(cbuffer) << endl;charMap* new_cm = new charMap();new_cm->key = cbuffer;new_cm->p = nyt->p_right;new_cm->value = getHuffmanCode(nyt->p_right);buffers.push_back(*new_cm);Node *root = nyt->p_parent;weightAdd(root);nyt = nyt->p_left;}}}void HuffmanTree::weightAdd(Node * p_node)
{while (p_node != nullptr) {Node* large = findLarge(p_node);if (large != p_node && !tree.isAncestor(p_node, large)) { 			tree.swap(large, p_node);int temp;temp = large->num;large->num = p_node->num;p_node->num = temp;for (auto iterator = buffers.begin(); iterator != buffers.end(); iterator++) {iterator->value = getHuffmanCode(iterator->p);}}p_node->weight++;		p_node = p_node->p_parent;}
}void HuffmanTree::decode(string input)
{Node *nyt = tree.getRoot();int p = 0;int l = 1;string temp;bool exit = false;for (;p+l<= input.length();){exit = false;temp = input.substr(p, l);cout << "\n循环: " << temp ;//如果是NYT，说明有新的if (temp == getHuffmanCode(nyt)) {p+=l;l = 5;temp = input.substr(p, l);//在字典中寻找对应值for (auto iter = initCode.begin(); iter != initCode.end(); ++iter) {string cur = iter->second;if (cur == temp){//找到了就加新的cout << "      新码的:" << iter->first << endl;Node *c = new Node(nullptr, nullptr, nyt);c->num = sum++;c->weight = 1;Node *NYT = new Node(nullptr, nullptr, nyt);NYT->num = sum++;NYT->weight = 0;tree.addNode(nyt, NYT, BinaryTree::LeftChild);tree.addNode(nyt, c, BinaryTree::RightChild);nyt->weight = 1;charMap* new_cm = new charMap();new_cm->key = iter->first;new_cm->p = nyt->p_right;new_cm->value = getHuffmanCode(nyt->p_right);buffers.push_back(*new_cm);//依次增加权重Node *root = nyt->p_parent;weightAdd(root);//设置新的nyt节点为原nyt节点的左孩子nyt = nyt->p_left;}}p += l;l = 1;exit = true;}else//如果不是NYT，就在树里面找{auto existNode = buffers.begin();for (existNode; existNode != buffers.end(); existNode++) {if (existNode->value == temp) {//找到cout  << "     在树中存在，为： " << existNode->key << endl;Node *root = existNode->p;weightAdd(root);p += l;l = 1;exit = true;break;}}}//如果即不再树中也不在字典中，l++if(!exit)l++;}}//主函数程序
int main()
{HuffmanTree huff;//这个字典是初始编码表initCode['A'] = "00001";initCode['B'] = "00010";initCode['C'] = "00011";initCode['D'] = "00100";string input = "ABBCADAD";huff.encode(input);//进行编码的函数//以下是解码函数HuffmanTree dhuff;dhuff.decode("0000010000100100000110110000100111001");system("PAUSE");return 0;
}

.h头文件 代码片.

#pragma once
#include <fstream>
#include<iostream>
#include<vector>
#include<queue>
#include<stack>
#include<string>using namespace std;struct Node {int weight; int num;  Node* p_left; Node* p_right;  Node* p_parent; Node(Node* p_left, Node* p_right, Node* p_parent) : p_left(p_left), p_right(p_right), p_parent(p_parent) {};
};class BinaryTree
{
public:enum Brother { LeftChild, RightChild };BinaryTree(int num = 0, int weight = 0);~BinaryTree();bool swap(Node* p_nodeA, Node* p_nodeB);bool addNode(Node* p_parent, Node* p_child, Brother brotherState);Node* findNode(string in);void deleteNode(Node *p_node);Node* getRoot() { return p_root; }Brother getBrotherState(Node *p_node);bool isAncestor(Node* p_nodeChild, Node* p_nodeAncestor);
private:Node *p_root;};class HuffmanTree
{
public:int sum;HuffmanTree();void encode(string input);void weightAdd(Node* p_node);void decode(string input);BinaryTree tree;struct charMap {char key;std::string value;Node* p;};vector<charMap> buffers;string getHuffmanCode(Node *p);Node * findLarge(Node *);};
  • 源代码修改自https://blog.csdn.net/qq_36533706/article/details/80381457?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522163819021616780366596114%2522%252C%2522scm%2522%253A%252220140713.130102334…%2522%257D&request_id=163819021616780366596114&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2allsobaiduend~default-2-80381457.first_rank_v2_pc_rank_v29&utm_term=%E8%87%AA%E9%80%82%E5%BA%94Huffman%E7%BC%96%E7%A0%81&spm=1018.2226.3001.4187

http://chatgpt.dhexx.cn/article/6nbHPDjU.shtml

相关文章

huffman python,哈夫曼(Huffman)编码python代码实现

huffman python,哈夫曼(Huffman)编码python代码实现

首先看定义 哈夫曼编码(Huffman Coding)&#xff0c;又称霍夫曼编码&#xff0c;是一种编码方式&#xff0c;哈夫曼编码是可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法&#xff0c;该方法完全依据字符出现概率来构造异字头的平均长度最短的码字&#xff0c;有时称…
阅读更多...
Huffman Tree

Huffman Tree

Huffman Tree 哈夫曼树&#xff1b;哈夫曼编码&#xff1b;最优二叉树 自底向上 变长编码&#xff1b;前缀编码&#xff1b;熵编码 数据无损压缩&#xff1b;最短编码&#xff1b;最佳判定树 一、基本概念 Huffman Tree&#xff0c;又称最优二叉树&#xff0c;是带权路径长度最…
阅读更多...
Huffman Codes

Huffman Codes

题目 In 1953, David A. Huffman published his paper “A Method for the Construction of Minimum-Redundancy Codes”,and hence printed his name in the history of computer science. As a professor who gives the final exam problem on Huffman codes, I am encounte…
阅读更多...
HuffmanTree

HuffmanTree

#include "stdafx.h" #include "stdio.h" #include "stdlib.h" #include "string.h"typedef int ELEMTYPE;//哈弗曼树节点结构体 typedef struct HuffmanTree {ELEMTYPE weight;ELEMTYPE id;//区分权值相同的节点struct HuffmanTree* …
阅读更多...
JPEG中Huffman解码实例讲解

JPEG中Huffman解码实例讲解

DHT Huffuman表格式 -------------------------------------------------------------------------- 名称 字节数 值 说明 -------------------------------------------------------------------------- 段标识 1 FF 段类型 1 C4 段…
阅读更多...
哈夫曼树（huffman）

哈夫曼树（huffman）

学完了huffman树&#xff0c;讲一下自己对它的理解 huffman树遵循二叉树的原则&#xff0c;每个节点最多有两个子节点&#xff0c;但是每个节点都带有一个权重&#xff0c;如果我们要将一组字符串 “ B D C A F E ” 插入huffman树&#xff0c;每个字符都会带有一个权重&#…
阅读更多...
Huffman树和Huffman编码

Huffman树和Huffman编码

文章目录 Huffman树的定义带权路径长度WPL Huffman树的构造Huffman树的特点 Huffman编码构造Huffman编码 Huffman树的定义 哈夫曼&#xff08;Huffman&#xff09;树&#xff0c;又称最优二叉树&#xff0c;是一类带权路径长度WPL最短的树。 带权路径长度WPL 要理解带权路径…
阅读更多...
Huffman树（哈夫曼树）

Huffman树（哈夫曼树）

哈夫曼树又称最优二叉树&#xff0c;是一种带权路径长度最短的二叉树。所谓树的带权路径长度&#xff0c;就是树中所有的叶结点的权值乘上其到根结点的路径长度&#xff08;若根结点为0层&#xff0c;叶结点到根结点的路径长度为叶结点的层数&#xff09;。树的带权路径长度记为…
阅读更多...
虚拟机下安装BackTrack5 (BT5)教程及BT5汉化

虚拟机下安装BackTrack5 (BT5)教程及BT5汉化

isare邀请您访问Backtrack中文网 http://www.backtrack.org.cn/?fromuid50397 isare邀请您访问Backtrack中文网 http://www.backtrack.org.cn/?fromuserisare PS&#xff1a;back track 安装过程中有2点要注意&#xff1a;第一&#xff1a;复制到99%的时候会等大约10来分钟&a…
阅读更多...
bt 下载工具 deluge 配置 优化 使用

bt 下载工具 deluge 配置 优化 使用

目录 Ubuntu 18 配置 deluge Deluge 安卓远程客户端 Deluge 性能调优 deluge是基于libtorrentpython的跨平台bt/pt客户端&#xff0c;适合在Linux环境下使用 deluge完全开源免费&#xff0c;对IPv6支持良好&#xff0c;性能优于transmission&#xff1b;在嵌入式设备上使用d…
阅读更多...
BT5的U盘完整安装

BT5的U盘完整安装

BT5是什么就不用多说了&#xff0c;从网上看了许多教程&#xff0c;大多是利用unetbootin工具将ISO文件直接解压到U盘上&#xff0c;这样并不能完全使用BT&#xff0c;保存好的文件&#xff0c;重启机器后就没了&#xff0c;其实就是当做光盘使用了&#xff0c;另外还有一个方法…
阅读更多...
有哪些好用的BT下载器？

有哪些好用的BT下载器？

​​​​​​2022年5个好用的 BT/ 磁力链接下载工具推荐 &#xff5c;Windows 、安卓系统 | 科技雷达 A full-featured download manager
阅读更多...
BT是如何下载的

BT是如何下载的

BT协议简介 一、BT下载是怎么来的&#xff1f; 在互联网上下载文件的方式大概有这么几种&#xff1a;FTP、HTTP、BT、eMule(电驴)等&#xff0c; 浏览器会直接支持FTP和HTTP下载&#xff0c;BT和eMule下载一般需要专用的下载软件的支持。 接下来分别简单介绍一下他们的区别&…
阅读更多...
ed2k下载

ed2k下载

ed2k下载 在下载ed2k资源的时候&#xff0c;浏览器一般不能直接下载&#xff0c;这个时候该怎么办呢&#xff1f; 方法一&#xff1a;下载迅雷&#xff0c;直接安装 方法二&#xff1a;使用在线工具&#xff0c;将链接转化为别的形式 https://tool.lu/urlconvert/ 方法三&am…
阅读更多...
BT是怎么下载的

BT是怎么下载的

BT协议简介 一、BT下载是怎么来的？ 在互联网上下载文件的方式大概有这么几种：FTP、HTTP、BT、eMule(电驴)等， 浏览器会直接支持FTP和HTTP下载，BT和eMule下载一般需要专用的下载软件的支持。 接下来分别简单介绍一下他们的区别： FTP 是 File Transfer Protocol（文件…
阅读更多...
最好用的bt下载器qbittorrent下载安装使用教程

最好用的bt下载器qbittorrent下载安装使用教程

qBittorrent绝对是我心目中BT下载工具中的NO.1&#xff0c;虽说我平时也会用迅雷下载国内的某些资源&#xff0c;但是仍然不妨碍它是我心目中的主力下载神器&#xff01;它可以说是我最早接触的除迅雷之外的一款BT下载神器。它是完全免费的种子和磁力链接下载工具&#xff0c;最…
阅读更多...
BT5 WIFI破解

BT5 WIFI破解

实验环境 VMwareWorkstation 9.0 BackTrack5 R3-GNOME-32 工具说明 VMware&#xff1a;著名的虚拟机软件&#xff0c;本实验采用虚拟机环境下安装BackTrack。 BackTrack&#xff1a;是一个基于Ubuntu GNU/Linux的发行版本&#xff0c;主要用做数字取证和入侵测试。其无线安全审…
阅读更多...
BT5下载地址

BT5下载地址

http://www.backtrack-linux.org/downloads/ 下载方法&#xff1a; 1,先填写好网页里的三个框,如: Your Name(你的名字): ABC Email Address(邮箱): ABC163.com Country(国家): china 2,然后点"download" 3,按照自己的…
阅读更多...
最全BT介绍

最全BT介绍

BitTorrent 简介 riba2534 2021年04月11日 19:26 阅读 851 关注 BitTorrent 简介 从 P2P 说起 经常在网上飙车的老司机应该都知道 BT 下载&#xff0c;但是有时候拿到了种子却下载不动&#xff0c;会不会很抓狂&#xff0c;是不是还觉得是自己网不行&#xff0c;那作为一…
阅读更多...
034_Unicode标准

034_Unicode标准

1. Unicode标准 1.1. 由于ASCII字符集、ISO字符集、GBK字符集列出的字符集都有容量限制, 而且不兼容多语言环境, Unicode联盟开发了Unicode标准。 1.2. Unicode标准涵盖了世界上的所有字符、标点和符号。 1.3. 不论是何种平台、程序或语言, Unicode都能够进行文本数据的处理…
阅读更多...
推荐文章

Copyright @ 2022~2023