基本原理

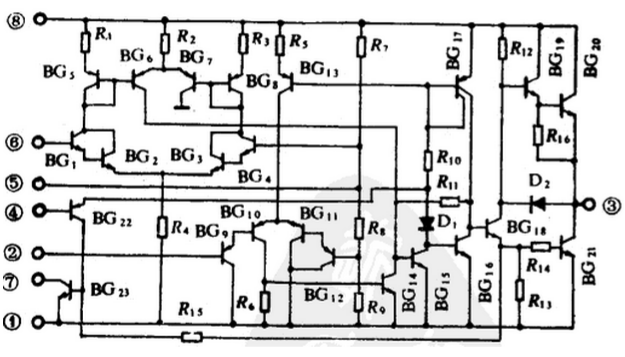
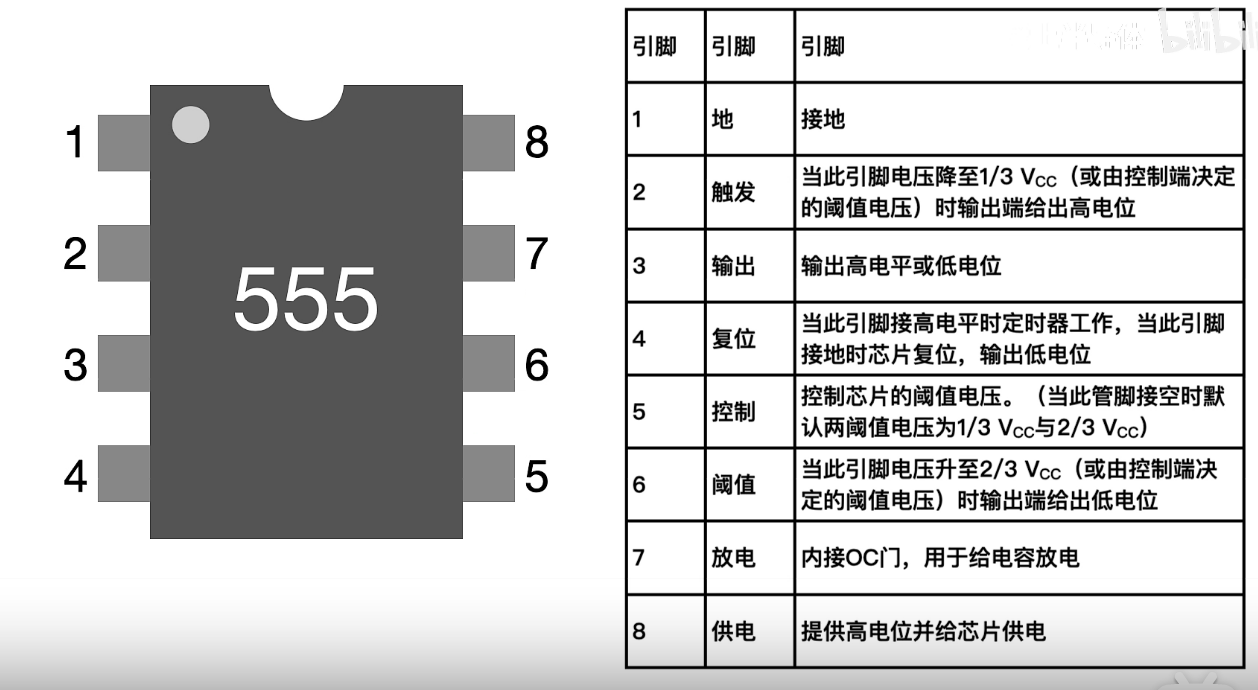
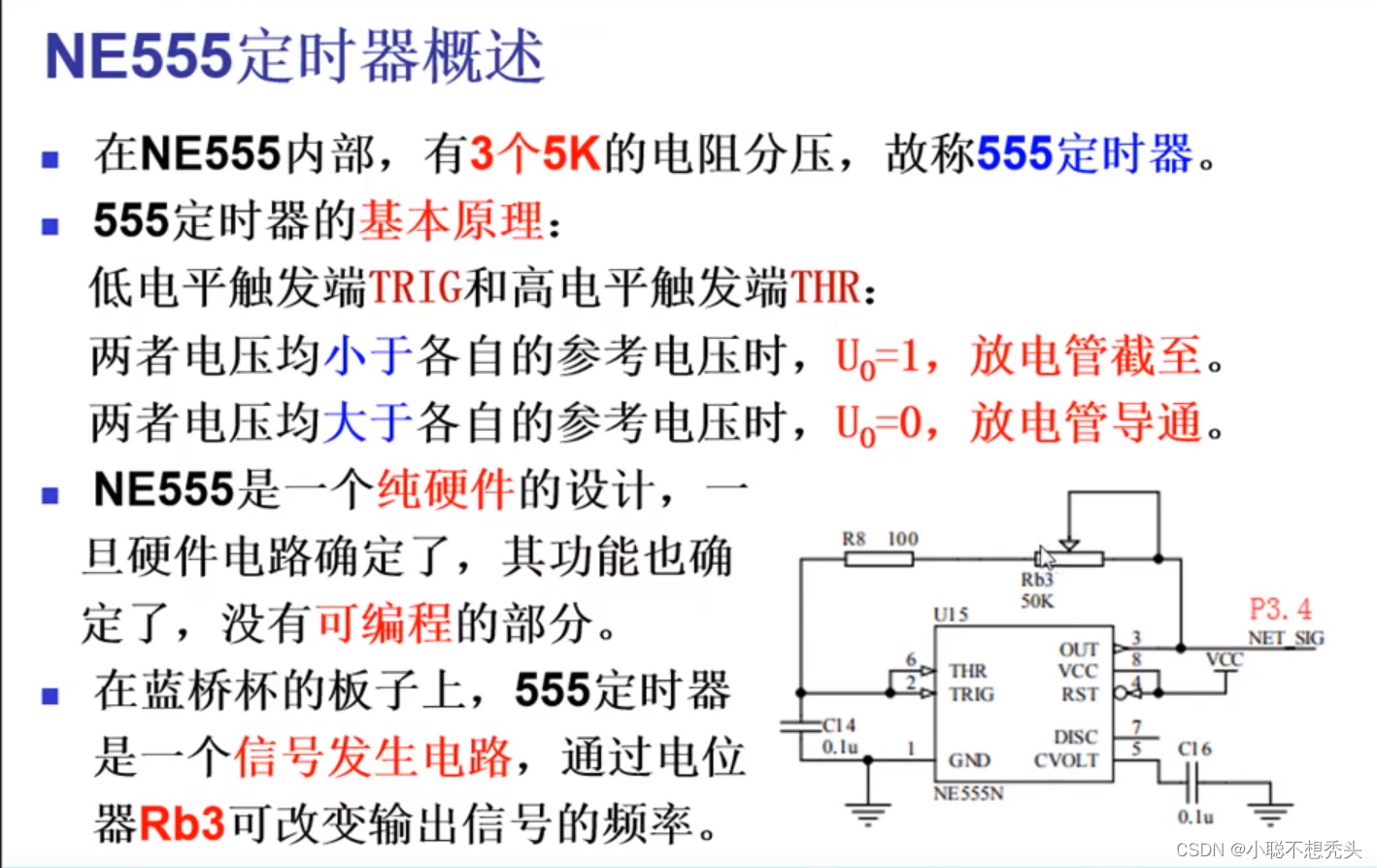
NE555主要由分压电路，电压比较器，RS触发器三部分组成；

分压电路	电压比较器	RS触发器
提供电压比较器比较电压	根据触发信号输出高低电平	用于输出矩形波

当$V_A>\frac{2}{3}{V}_{cc}$,$C_1$输出低电平，反之输出高电平。
当$V_B>\frac{1}{3}{V}_{cc}$,$C_1$输出高电平，反之输出低电平。
$C_1$触发器输出端接RS触发器Reset引脚,低电平有效。
$C_2$触发器输出端接RS触发器Set引脚,低电平有效。

$V_A$	$V_B$	$R$	$S$	$Q$	放电管
$>\frac{2}{3}{V}_{cc}$	$>\frac{1}{3}{V}_{cc}$	0	1	0	导通
$<\frac{2}{3}{V}_{cc}$	$>\frac{1}{3}{V}_{cc}$	1	1	保持原状态	保持原状态
$<\frac{2}{3}{V}_{cc}$	$<\frac{1}{3}{V}_{cc}$	1	0	1	截至

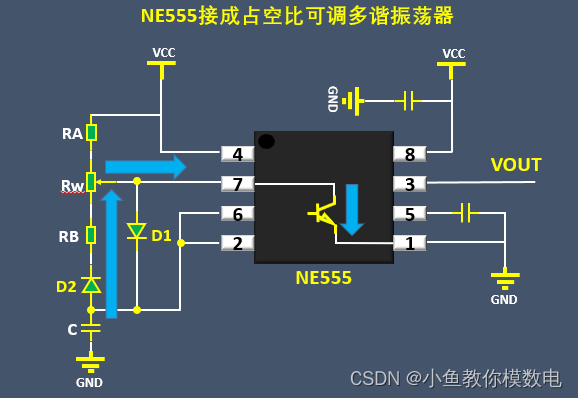
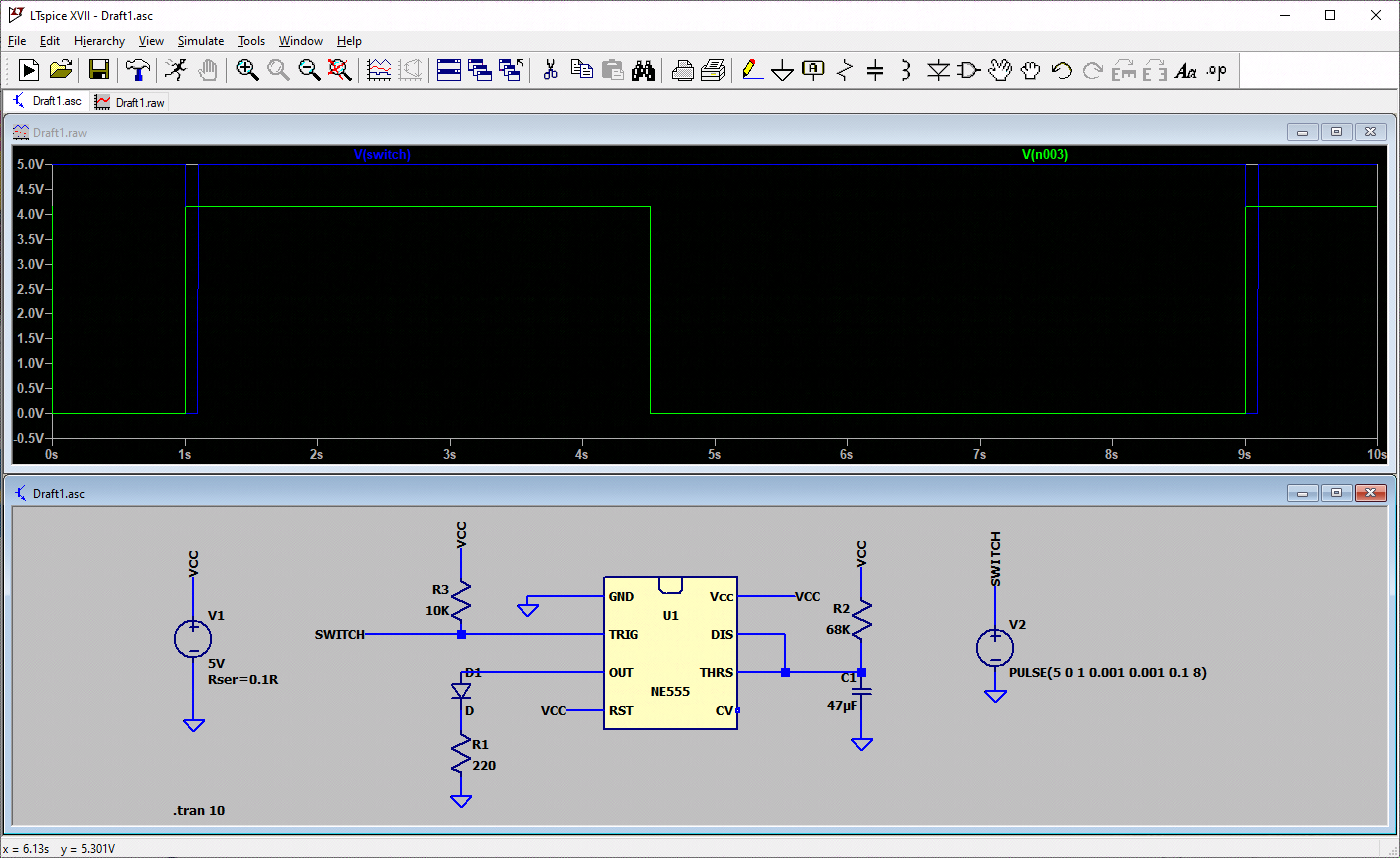
该图为数据手册中输出为方波的多谐振荡器。
把它代入到原理图中进行分析。

$V_A=V_B$	$R$	$S$	$Q$	放电管	电容(6脚与地之间)
0V	1	0	1	截至	充电
$>\frac{1}{3}{V}_{cc}$	1	1	保持原状态	保持原状态	充电
$>\frac{2}{3}{V}_{cc}$	0	1	0	导通	放电
$<\frac{2}{3}{V}_{cc}$	1	1	保持原状态	保持原状态	放电
$<\frac{1}{3}{V}_{cc}$	1	0	1	截至	充电

电源接通时电容从$0V$开始充电,
电容电压达到$\frac{2}{3}{V}_{CC}$时，输出状态发生变化，电容通过$R_2$和导通后的放电管开始放电。
当放电到低于$\frac{1}{3}{V}_{CC}$时，放电管截至，电容继续开始充电。
通过电容充放电的循环过程产生矩形波。

公式推导

根据一阶电路的三要素公式：
$f(t)=f(\infty )+[f(0_{+})-f(\infty )]\ast e^{\frac{t}{\tau }}$

$t=RC{\ln }_{}\frac{f(0_{+})-f(\infty )}{f(t)-f(\infty )}$
$f(0_{+})$:初始值
$f(\infty )$:稳态值
$f(t)$：充放电的目标值

由$V_{CC}$经过$R1、R2$给电容由$\frac{1}{3}{V}_{CC}$充电到$\frac{2}{3}{V}_{CC}$
初始值为：$\frac{1}{3}{V}_{CC}$
稳态值为：$V_{CC}$
目标值为：$\frac{2}{3}{V}_{CC}$

代入公式：
$th=(R1+R2)C{\ln }_{}\frac{\frac{1}{3}{V}_{CC}-V_{CC}}{\frac{2}{3}{V}_{CC}-V_{CC}}$
$th=(R1+R2)C{\ln }_{}\frac{\frac{2}{3}{V}_{CC}}{\frac{1}{3}{V}_{CC}}$
$th=(R1+R2)C{\ln }_{}2$
$th=(R1+R2)C\ast 0.693$
充电过程中Q为高电平,所以$th$为高电平输出时间。

放电管导通，电容经$R2$接地放电，由$\frac{2}{3}{V}_{CC}$放电到$\frac{1}{3}{V}_{CC}$
初始值为：$\frac{2}{3}{V}_{CC}$
稳态值为：$0V$
目标值为：$\frac{1}{3}{V}_{CC}$
代入公式：
$th=(R1+R2)C{\ln }_{}\frac{\frac{2}{3}{V}_{CC}-0}{\frac{1}{3}{V}_{CC}-0}$
$tl=R2\ast C{\ln }_{}\frac{\frac{2}{3}{V}_{CC}}{\frac{1}{3}{V}_{CC}}$
$tl=R2\ast C{\ln }_{}2$
$tl=R2\ast C\ast 0.693$
放电过程中Q为低电平，所以$tl$为低电平输出时间

推导出：
周期：$T=th+tl=(R1+2R2)C\ast 0.693$

频率：$f=\frac{1}{T}=\frac{1.44}{(R1+2R2)C}$

占空比：$D=\frac{tl}{T}=\frac{R2}{R1+2R2}$

通过调节$R1、R2、C$可以改变频率或者周期，调节$R2$可以调节占空比。

按照上面接法，$Q$端输出矩形波，电容端输出锯齿波。