最近一直在看Honey Badger BFT共识协议，看了很多博客和一些相关的论文，但是发现有些博客存在着部分理解错误的地方，或者就是直接翻译2016年的那一篇论文，在经过半个多月的细读之后，打算整理出这篇博客，方便给学习这个共识协议的人学习，同时自己也留存一份笔记，以下仅是笔者通过阅读论文和博客等方式，描述自己对Honey Badger的理解。如有错误，还请指正。
Miller等人提出的Honey Badger BFT是一种在异步网络环境下可以正常运行的BFT协议。

• 异步，比PBFT的吞吐量和延迟性能好
• 仅支持封闭网络，即主机个数已知，协议执行过程中没有新的主机接入网络。
• 无Leader，每个节点都可作为共识的发起者。
  Honey Badger BFT使用了两个方法来提升共识效率：
• 通过纠删码分割交易来环节单节点带宽瓶颈。
• 通过在批量交易中选择随机交易块，并配合门限加密来提升交易的吞吐量。

基础知识

纠删码

（我是在一篇博客上面看到的关于RS纠删码的介绍，这里只是粗略的介绍一个概念，让大家知道是用来干什么的，以及是一个什么原理。纠删码技术在后面的RBC阶段会使用到，主要是用于均分带宽，缓解提出共识交易节点的带宽瓶颈。）
纠删码工作原理简介：
RS（Reed-solomom）码是一种比较常见的纠删码，它的两个参数m和n分别代表校验块个数和原始数据块个数（课容忍m个数据块的丢失，拜占庭共识中，设m = 2f，原始数据块为f+1），我们可以使用n数据块就恢复出原始的数据块。
纠删码编码过程：C代表校验块，D代表原始的数据块。

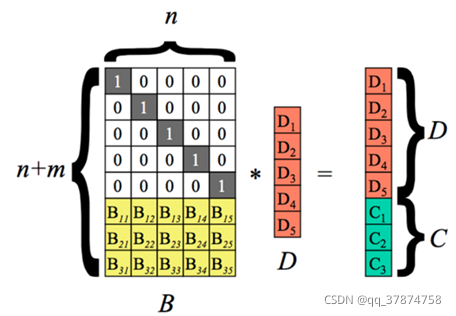
假设我丢失了D1、D4、C2数据块：

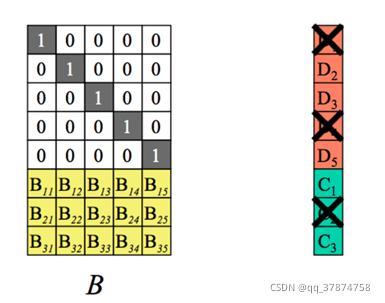
解码过程：（一共三步）
Step1：在编码矩阵中去掉求实数据块以及该数据块对应的行。即B矩阵变为了n*n维度的方阵，C和D组合的矩阵由（n+m）行变为n行，在上诉假设过程中，我们得到新的矩阵以及对应的矩阵运算关系式，其中在丢失了部分数据块后，D所代表的原始数据块成为了要求的目标。
step2：求B’的逆矩阵：
如下图所示：

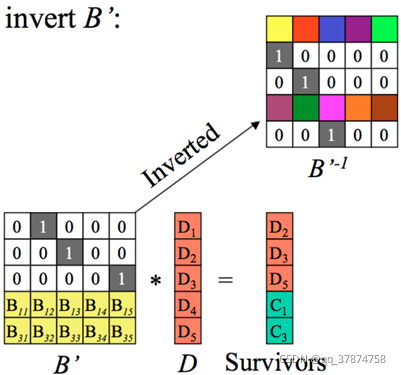
step3:可以采用对等式两边同时乘上B’的逆矩阵，于是得到所求解。


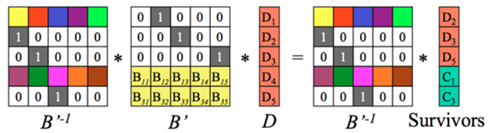
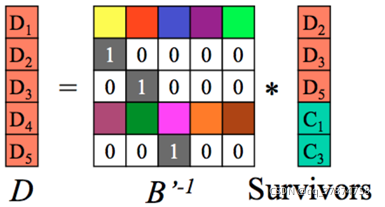
如果大家没太看懂，我贴上关于纠删码部分原作者的博客链接：

https://www.cnblogs.com/Robin5/p/11710005.html

随机交易块

为了降低各个节点之间提交交易的重复性，Honey Badger BFT算法使用随机选择交易块的方法来选择需要共识的交易集，具体选择条件如下：
假设网络中共有N个节点，每个节点进行共识的交易大小为B。每个节点收集交易数据，放到自身的交易缓冲池中，每一轮共识之前，节点从交易缓冲池的第一个B大小的交易池中随机选取 B/N 个交易进行共识。（提问：为什么节点只选择B/N个交易进行共识？答：因为不止一个节点提交共识交易集，是所有节点都会进行提交，当前节点 Pi 会从其他N-1个节点处收到他们提交的交易集，然而每个节点能够共识的交易大小为B，N * B/N = B，所以知道了么？）

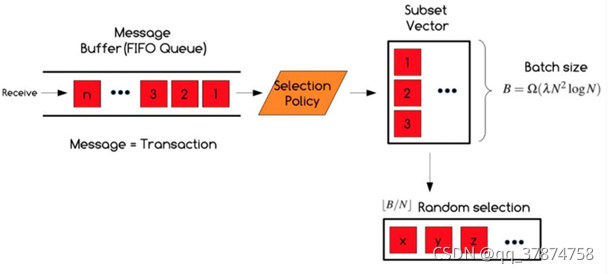
门限加密

第三方可信机构（2016年的论文提出：如果可信机构不可信了，可以使用分布式密钥生成协议替代）会将私钥分片放给所有参与共识的节点，在解密的时候，只要节点收集到一定门限数量的解密分片，则该节点可以恢复出密文。使用门限加密还可以实现审查弹性，避免了敌手知道哪个交易由哪个节点发起而阻挠共识的达成。

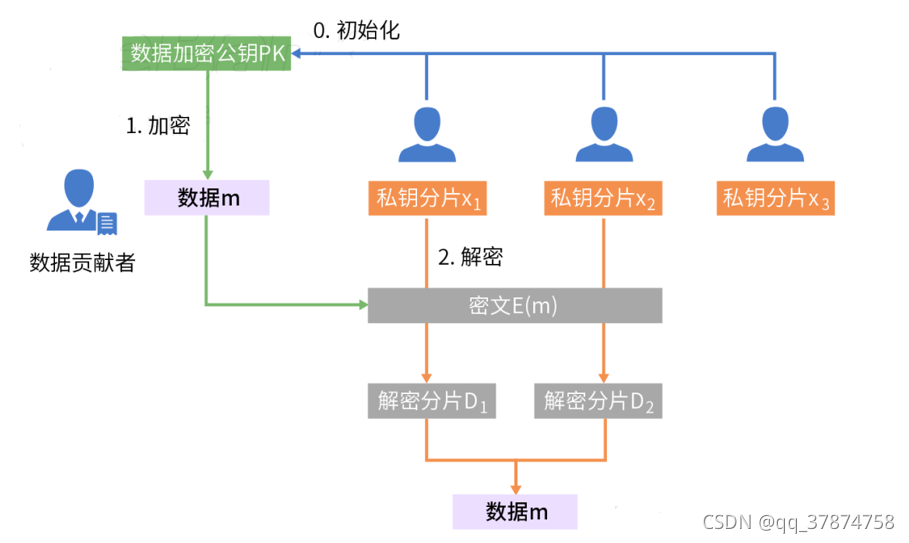
默克尔树

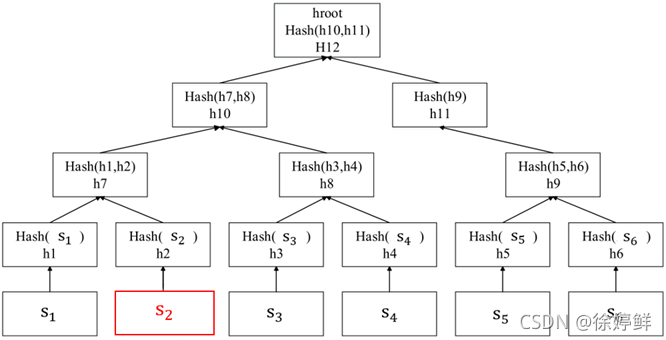
默克尔树会在后面的RBC协议阶段使用到。默克尔树（或者哈希树）是一棵能够存储哈希值的树，树的叶子节点是数据块（例如交易集、文件等）的哈希值，内部节点则是其对应子节点串联字符串的哈希值。这里以RBC中的交易块 sj 为例。
如何校验数据块的叶子节点 sj 和路径 bj 校验是否等于 h，假设 j = 2，交易分块 s2，b2 以及 h，b2 = {h1, h8, h11}

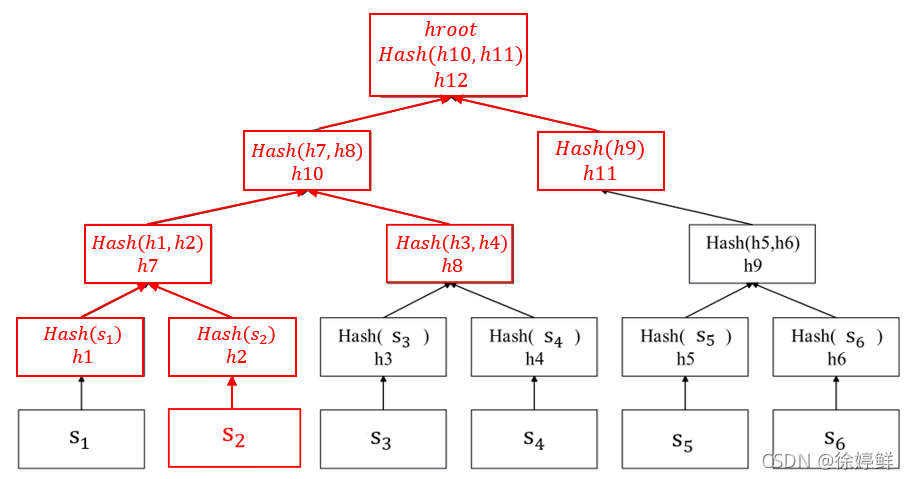
Honey Badger BFT算法总流程

总体的算法主要包括三个步骤：

• 随机选取交易集并对交易集加密
• 交易的可靠广播（采用RBC实现）。
• 共识（采用ABA实现）
  算法流程如下
• 节点 Pi 先根据随机选择交易块的选择规则选取要进行共识的交易集合（B/N个交易），第三方可信机构分发私钥分片给每个节点。
• 节点 Pi 使用公钥PK对交易集进行加密，加密的交易用 x 表示。
• 将 x 作为ACS（后面会详细讲解）的输入，ACS结束后，会收到N个（包括自己的那一个，其余为其他节点发起的交易共识）交易集 vj ，以及交易对应的01比特串，每个比特对应一个节点发起的共识交易集合（1表示该交易集最终会被提交，0表示该交易集不会被提交）。
• 将二进制共识结果为 1 的交易块收集起来，并对它进行解密，当 Pi 收到 f + 1个解密分片的时候 Pi 就可以解密得到 vj 的明文交易集合。交易被解密之后，会进行赛重、校验交易正确性、和排序等环节。交易被提交之后，就会从待提交的交易缓冲池中删除。

下图为Honey Badger BFT算法总流程图（运行于Pi）。

ACS（异步公共子集协议）

Hoeny Badger BFT是第一个实现最佳渐近效率的一步原子广播协议。
Honey Badger BFT算法采用ACS（Asynchronous Common Subset）协议实现了原子广播（Atomic Broadcast）。
ACS协议由两个协议组成：一个是可靠广播协议RBC（Reliable Broadcast），一个是异步二进制协议ABA（Asynchronous Binary Agreement）。

• RBC协议：广播交易。
• ABA协议：形成一致的二进制交易列表。

下图为RBC和ABA协议具体执行过程：这只是在 Pi 为发起共识交易者的角度进行解释，其实其他的节点也是相同的步骤，并且并发执行。

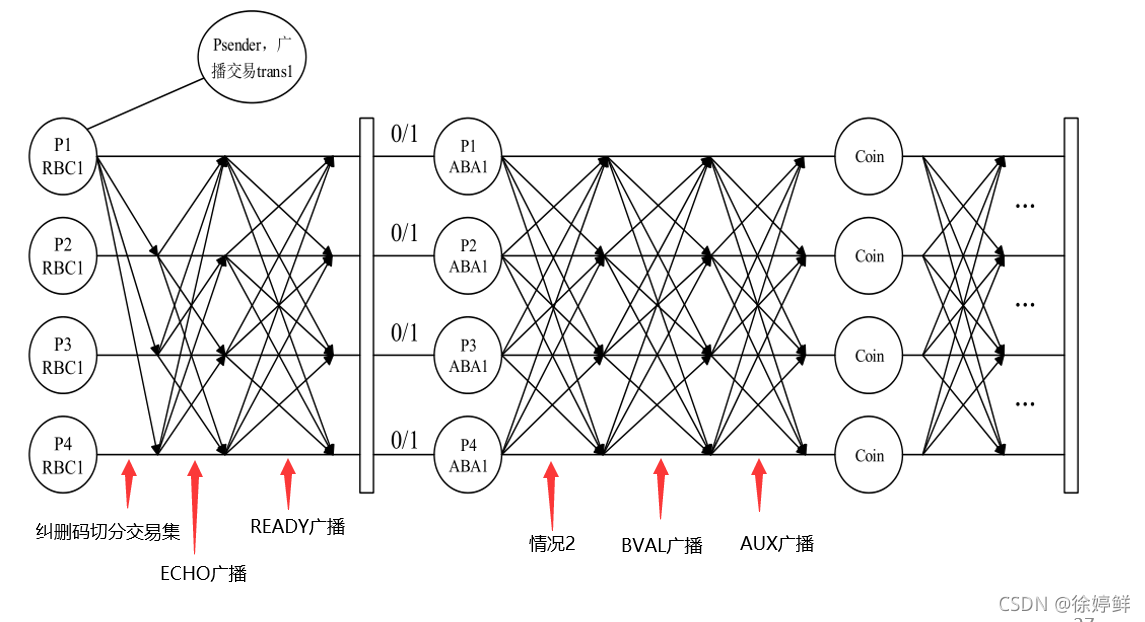
RBC协议

论文采用基于纠删码的RBC协议来广播每个节点提交的交易集。RBC的协议包括如下步骤（这里只是针对 Pi 为消息的发送者，其实其他的节点也在同时进行与 Pi 相同的步骤）：

• Pi 将加密后的交易块 v 作为RBC的输入，使用纠删码技术生成N个数据块 {sj}， j∈N。
• 将所有的 sj 计算出默克尔根 h， bj 是 sj 到 h 的路径，并将 VAL(h, bi, si) 消息广播给其他节点。（关于默克尔树部分的理解，可以参考前面基础知识关于其的介绍）
• 如果其他节点收到来自Pi的VAL信息，则广播 ECHO(h, bi, si) 消息。
• 当其他节点收到EHCO消息之后，他首先会校验根据 si 和 bi 是否能算出h（对 Pi 来说，就是校验 ECHO(h, bj, sj)），检查这个ECHO是否有效，如果能够正确推算，就表示此ECHO有效，如果无效则直接丢弃这个ECHO。
• 当节点收到 2f+1 个ECHO消息（h相同）之后，则选取其中 f+1 个ECHO，根据其sj 和 bj计算出 h’。然后对比 h’ 和 h 是否相等。如果相等则广播 REDAY(h) 消息。
• 当节点收到 2f+1 个 READY(h) 消息，则使用前面收到的 f+1 个ECHO消息恢复出原始的密文 v（纠删码技术）。
  （注释：下图中算法的倒数第二个小圆点的部分。我没有在流程中叙述出来，肯定有人会有疑惑，根据我自己的理解，我认为这一部分是为那些网络情况不好的正确节点准备的，或许他们在收到了 f+1 个别的节点发出的READY(h)消息的时候，还没有收到足够多的ECHO消息，所以他自己本身还不能触发发送READY的契机。但是收到了那么多人已经发了READY消息，那么他就知道这个答案是对的，那么他就抄作业。直接发送READY消息，这也就解释了最后一个点为什么有wait for N-2f ECHO messages）。

ABA协议

如果节点能够根据 f+1 个ECHO消息重构出交易密文 v，则对对应的实例ABA发送一个1，如果当前节点已经重构出了 2f+1 个节点提交的交易块（指已经输入了2f+1个1），那么就会对后面所有的ABA实例都输入0，表示在收到 2f+1个交易块之后，后面的我都不要了。
（为啥这么任性？因为这是在拜占庭共识中，会有 f 个是拜占庭节点，如果我要等到全部节点的交易块都收到再进行下一步，其实是不太可能的，万一有拜占庭节点故意不发，那样我们的等待很可能会阻塞共识的达成，所以我们就假设排除掉 f 个个节点的交易，只收到2f+1个就行啦）。
其实这里会有一个情况2（当然接下来只是我的理解，如ACS的第一个图中我标注的情况2这个阶段所示）。一个节点已经对2f+1个ABA实例输入1，对剩下的 ABA 实例都为0，但是这时候所有节点输入为 1 的ABA实例的集合其实并不相同，所以需要一次交互，当节点对某个 ABA 实例设置为0，但是他又收到了 f+1 个其他节点发来将该实例设置为1的消息，那么他就会把自己设置为0的ABA实例重新设置为1，并且他还需要等待该实例对应的交易集从RBC中重构出来。如果没有收到那么多1，那就不更新。

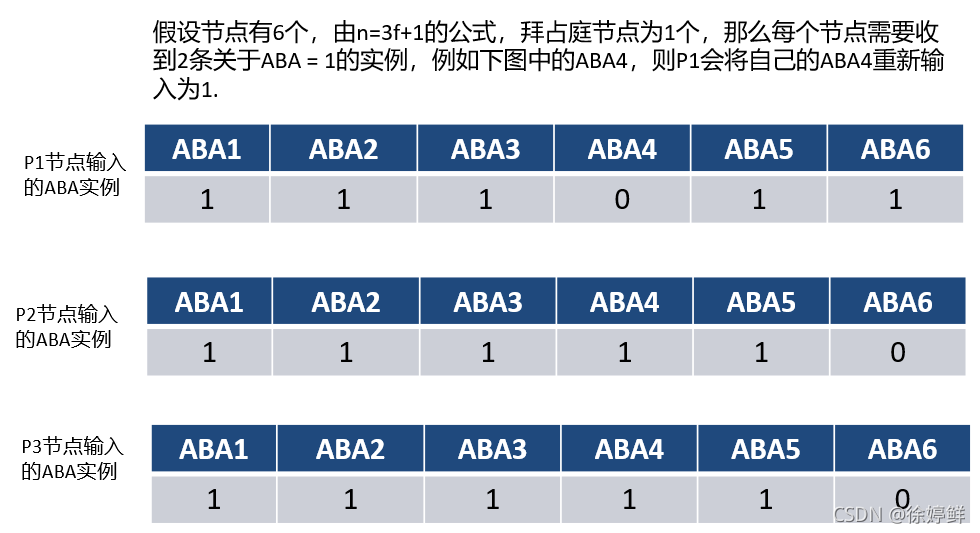
假设节点P1经过前一轮的交互，已经将自己拥有的ABA实例对应的二进制序列更新，此时我们以ABA2为例。节点对应的其他ABA实例也是相同的步骤，其他节点也与P1并行执行。r表示轮次，会根据循环的轮次而不断自增。

1. est1初始化为1
2. 广播BVAL1(1)
3. bin_values1 = ∅
4. 在节点P1接收 2f+1个到BVAL1(1)，则bin_values1= bin_values1∪{1} = {1}
5. 当bin_values1 不为空集的时候：

※ 广播AUX1(w)，w是属于集合bin_values1里面的元素，这时候bin_values1里面只有一个元素——1，所以所有节点在bin_values1里面选的的元素w必然相同。
※ vals表示所有节点选取的w的集合，当前为第一轮，vals集合里面也只会有元素1
※ s 可以看做是一个随机数，其实它就是所有节点将轮次 r 进行门限签名再聚合之后形成的聚合签名。
※ 这时vals集合是与{b} = {1}相等的，那么他会进入下面的那个if语句，est2 = 1，如何当前的1与随机抛硬币算法选取出的结果相等，那么表示已经对这个交易块的提交达成了共识，输入当前的共识结果1。（s%2 ∈{0,1}）
※ 如果不凑巧与抛硬币算法没有相等，那会在进入一次上面的循环。随着循环的次数越多，会更容易达成共识。

其实这一部分给我的感觉就是：节点之间选出一个结果，然后还需要老天爷（随机数）来决定你这个结果要不要被采纳。相同就采纳，不相同就不采纳。但是这个2016年那篇论文中提到了已经证明了在常数轮次可以达成最终的共识。

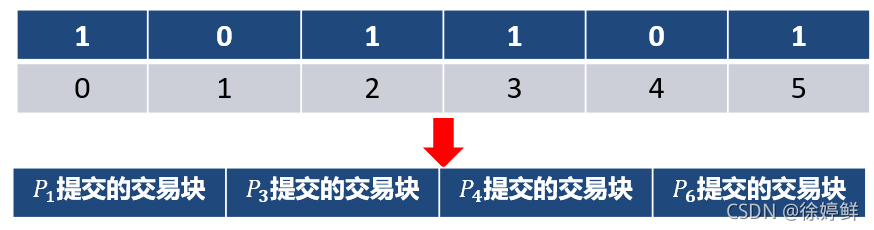
最后经过ABA协议之后，得到一串共识后的二进制列表（假设二进制列表是存储在数组中，文中没有提及，只是我的猜想）。再对收到的交易序列按照二进制列表的结果进行处理，下图中第一排为二进制列表，第二排位对应的节点下标。将为1的交易集提取出来，使用门限解密密钥进行解密，当收到 f+1个对应同一个交易集的解密分片的时候，就可以解密出当前的交易集。在进行一系列的交易去重、验证交易正确性的手段。然后将最终的交易集进行提交。并从每个节点的待提交交易缓存池中将提交成功的交易删除。

以上只是我这段时间自己学习和理解的Honey Badger BFT，如有不对之处，还望指出。
附上的2016年的Honey Badger BFT原文，以及门限加密原文，以及参考的ABA算法的原文可以在我的博客主页找到。