没有免费午餐定理No Free Lunch Theorem

不得不说，网上博客千千万，在技术方面，我承认这些博客的重要性。然而，只要和机器学习理论挂钩，似乎都讲得不清不楚，大家都是各自地抄，抄书籍，抄论文，抄别人的博客或者直接翻译，或者讲故事一样描述，几乎没什么太深入的理解，给人的感觉是“哎？似乎是这样，我好像有一点懂了”，然后就没了，其实看这样的博客简直就是在浪费时间，凡是不能一次性地搞懂一点内容，都是扯犊子。总之，看了网上的关于机器学习博客的文章，我感觉很不理解，很困惑，很迷茫。所以我就推导了一遍周志华书籍《机器学习》没有免费午餐定理(No Free Lunch Theorem)的一个简单证明过程。

一、讲故事一样的描述

讲故事虽然并不严格，然而它还是有必要用这样的思维去描述这个定理。其用途是给别人普及，同时也方便自己记忆。

那么，如何像讲故事一样地描述没有免费午餐定理呢？最直观的，我们吃午饭都是要付钱的，哪怕有人请客，那请你吃饭的人也帮你付了钱。但这个似乎跟机器学习并没有半吊子关系。

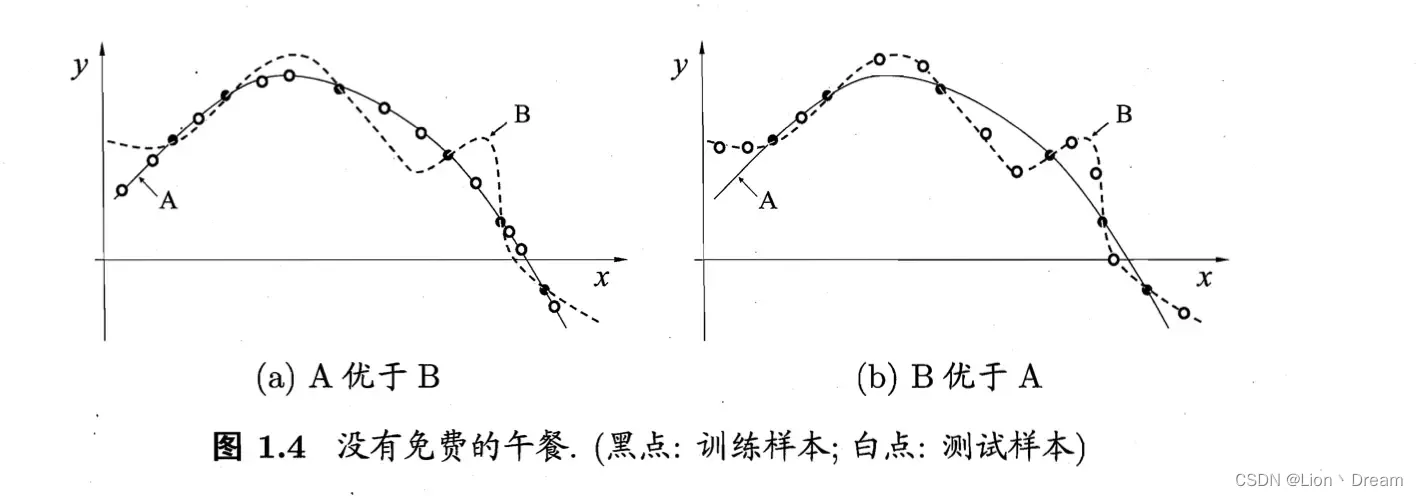
在机器学习领域里面，有一个雷打不动的定理，即没有免费午餐定理。它被描述为：没有一个学习算法可以在所有情况下总是产生最准确的模型。也就是说，不管采用何种学习算法，至少存在一个模型，比随机猜测算法得到的模型要差。这个定理的最重要意义是，在脱离实际意义情况下，空泛地谈论哪种算法好毫无意义，要谈论算法优劣必须针对具体学习问题。所以，我们在比较学习算法的时候，需要针对具体的学习问题。针对这个问题，学习算法a可能更好；而针对那个问题，学习算法b可能更好。

周志华在他的机器学习书籍里面说到，实际上在很多时候，我们只关注自己正在试图去解决的问题并它找到一个方案，而至于这个方案在其他问题上是否为好方案并不关心。例如，为了快速从A地到达B地，如果我们正考虑的A地是南京鼓楼，B地是南京新街口，那么骑自行车是一个很好的方案；如果A地是南京鼓楼，B地是北京故宫，那么骑自行车显然是一个极其糟糕的方案，但我们对此并不关心。

总之一句话，谈论算法的相对好坏，要针对具体的学习问题。而当你的算法在某个问题取得较好的性能时，那得注意了，请你说说你为这这么好的性能付出了什么代价？

二、相对严格的描述及其证明

这个定理之所以雷打不动，是因为它是经过严格的数学证明的。下面就顺着周志华机器学习书籍里面的内容，推导一遍其证明过程。

首先，我们来看看原文，如下。

看着这些公式，确实头都大了。不过不用怕，这充其量也就是高中数学的知识。求和公式、条件概率、均匀分布，这些不都很熟悉吗？我们高中就学过。只要我们把它展开，你就明白为什么会是这样的计算过程了。

先从公式（1.1）开始理解吧。

先看左边， $E_{ote}$ 表示机器学习算法 $\pounds _{a}$ 的训练集外误差，可以理解为测试集误差（因为测试集是拥有标记信息的，有标记信息才能计算误差，否则不能。由于训练集外读着很别扭，所以后文直接把训练集外的样本所构成的集合当作是测试集）；

机器学习算法 $\pounds _{a}$ 能够在训练集 $X$ 上学习得到多个机器学习模型，而一个模型就是一个假设 $h$ ，多个假设 $h$ 便构成机器学习算法 $\pounds _{a}$ 的假设空间；

$f$ 是希望学习得到的目标函数，输入一个样本，经过 $f$ ，那么就能够得到一个正确的标签。无论这个样本是在训练集上，还是在测试集上；

所以， $E_{ote}(\pounds_a|X,f)$ 是指给定训练集 $X$ 和目标函数 $f$ ，机器学习算法 $\pounds _{a}$ 的测试集误差。

再看右边。有两个求和符号，第一个求和符号是遍历机器学习算法 $\pounds _{a}$ 在训练集 $X$ 上所有可能的模型，第二个求和符号遍历所有测试集的样本。然后就和。把右边的两层求和公式展开，然后用另外一种方式化简，最终是可以把两个求和符号进行交换的。其中 $P(\mathbf{x})$ 是遍历到样本 $\mathbf{x}$ 的概率， $P(h|X,\pounds_a)$ 是机器学习算法 $\pounds _{a}$ 在训练集 $X$ 上产生假设 $h$ 的概率（记住，假设 $h$ 就是一个模型）。那个指示函数就不必说了，不等于就是假设 $h$ 预测错，等于就是假设 $h$ 预测正确。预测正确就不管，错了，就记录，然后加起来，最后构成测试集的误差。

现在再来看看公式（1.2）的计算过程。在开始之前，先说一下目标函数 $f$ ，这里的目标函数不再是固定的目标函数，而是要考虑所有可能的目标函数，这些目标函数也构成一个集合。好了，现在再来理一理思路，有一个训练集 $X$ ，有一个测试集 $T$ ，而 $X\cup T=\chi$ ，我们设计了一个机器学习算法 $\pounds _{a}$ ，任务是二分类任务。所以如果训练集+测试集有 $|\chi |$ 个样本，那么可能的目标函数 $f$ 就会有 $2^{|\chi |}$ 种个。

所以，要求得机器学习算法 $\pounds _{a}$ 的性能，还需要在公式（1.1）的基础上外加一层求和符号，以遍历所有有可能的目标函数 $f$ 。

那么，现在可以正式地推导这个过程了。具体如下

# 推导过程太长了，博客不是很方便看
# 详情见https://download.csdn.net/download/qq_36158230/20246322
# 主要思想：对求和公式展开，重组，利用概率论相关的知识化简

三、一个易于理解的例子

看了一长串的计算过程之后，来个直观的例子，那是最舒服的。具体如下：

给定 $\chi=\{\mathbf{x_1}, \mathbf{x_2}, \mathbf{x_3}\}$ ，训练集 $X=\{\mathbf{x_1}, \mathbf{x_2}\}$ ，测试集 $T=\{\mathbf{x_3}\}$ 。那么对于二分类问题： $\chi \rightarrow \{0,1\}$ ，目标函数 $f$ 有以下 $2^{|\chi |}=2^3=8$ 种。

给定训练集 $X=\{\mathbf{x_1}, \mathbf{x_2}\}$ ，根据机器学习算法 $\pounds _{a}$ ，得到的假设空间为 $\{h_1,h_2,h_3,h_4\}$ ；根据机器学习算法 $\pounds _{b}$ ，得到的假设空间为 $\{h_5,h_6,h_7,h_8\}$ 。方便起见，这里 $h_i$ 就等于 $f_i$ 。那么，现在我们利用公式（1.2）计算这两个算法的性能。由于测试集只有一个样例，即 $\mathbf{x}_3$ ，故 $P(\mathbf{x}_3)=1$ 。

对于机器学习算法 $\pounds _{a}$ ，假设每个模型被选中的概率相等，那么

$P(h_1|X,\pounds_a)=P(h_2|X,\pounds_a)=P(h_3|X,\pounds_a)=P(h_4|X,\pounds_a)=\frac{1}{4}$

而机器学习算法 $\pounds _{a}$ 对应的指示函数的值为

利用得出结论之前的公式（即公式（1.2）包含了三个求和符号的式子）计算，得到

$E_{ote}(\pounds_a|X,f)=1\times 1\times \frac{1}{4}+1\times 1\times \frac{1}{4}+...+1\times 1\times \frac{1}{4}=4=2^{|\chi|-1}=2^{3-1}=2^2$

同理，对于机器学习算法 $\pounds _{b}$ ，假设每个模型被选中的概率相等，那么

$P(h_5|X,\pounds_a)=P(h_6|X,\pounds_a)=P(h_7|X,\pounds_a)=P(h_8|X,\pounds_a)=\frac{1}{4}$

而机器学习算法 $\pounds _{b}$ 对应的指示函数的值为

利用得出结论之前的公式（即公式（1.2）包含了三个求和符号的式子）计算，得到

$E_{ote}(\pounds_b|X,f)=1\times 1\times \frac{1}{4}+1\times 1\times \frac{1}{4}+...+1\times 1\times \frac{1}{4}=4=2^{|\chi|-1}=2^{3-1}=2^2$

经过计算发现，两个学习算法的训练集外误差竟是一样的。

也许有人要站出来问了，你两个算法的假设空间太特殊了，万一这个例子是巧合呢？

那好，现在令 $\{h_1,h_2,h_3,h_4\}=\{f_2,f_4,f_6,f_8\}$ ， $\{h_5,h_6,h_7,h_8\}=\{f_1,f_3,f_5,f_7\}$ 。继续用上面的方法算一算，结果发现两个机器学习算法的训练集外误差计算结果还是一样的。但是又有人要说了，你的算法的假设还是太特殊了，万一还是巧合呢？

好，现在令机器学习算法 $\pounds _{a}$ 的假设空间为 $\{h_1,h_2,h_3\}=\{f_2,f_4,f_6\}$ ，机器学习算法 $\pounds _{b}$ 的假设空间为 $\{h_4,h_5,h_6,h_7,h_8\}=\{f_1,f_3,f_5,f_7,f_8\}$ 。现在再来用上面的方法算一算。这时 $P(\mathbf{x}_3)=1$ 不变，而

$P(h_1|X,\pounds_a)=P(h_2|X,\pounds_a)=P(h_3|X,\pounds_a)=\frac{1}{3}$

$\tiny P(h_4|X,\pounds_a)=P(h_5|X,\pounds_a)=P(h_6|X,\pounds_a)=P(h_7|X,\pounds_a)=P(h_8|X,\pounds_a)=\frac{1}{5}$

此时，这两个机器学习算法对应的指示函数表分别为

它们所对应的训练集外误差分别为

$E_{ote}(\pounds_a|X,f)=1\times 1\times \frac{1}{3}+1\times 1\times \frac{1}{3}+...+1\times 1\times \frac{1}{3}=4=2^{|\chi|-1}=2^{3-1}=2^2$

$E_{ote}(\pounds_b|X,f)=1\times 1\times \frac{1}{5}+1\times 1\times \frac{1}{5}+...+1\times 1\times \frac{1}{5}=4=2^{|\chi|-1}=2^{3-1}=2^2$

这时发现它们的计算结果依然是4(通过数指示函数表中“1”的个数，然后乘以 $P(h|X,\pounds)$ ，或者累加计算也行，结果是一样的)，真是神奇啊！当然了，你也可以举其他的例子计算一遍，质疑一下这个雷打不动的机器学习定理。不过我推导了一遍计算过程，也用例子算了好几回，反正我是信了。

四、推荐阅读+观看

1.(强推)浙大2021-机器学习_哔哩哔哩_bilibili

2.浙江大学-研究生机器学习课程-_哔哩哔哩_bilibili

3.参考资料第2条

五、结束语

码字之余，难免疏漏，欢迎点评指出改正。同时，码字不易，不喜勿喷，文明交流。毕竟是个人理解，所以写的东西很有可能有所疏漏，但是希望大家能够文明交流。爱与尊重。

花费两天找了一些资料理解这个没有免费午餐定理，再花费一天时间把我所理解的内容全部写在博客之上。确实，在理解和作笔记的过程，都是相当艰苦的。不过有了一定的理解之后，确实让人恍然大悟，感觉收获良多。一大堆写得很复杂的公式难以让人理解，实际上是由于它的跳跃性真的太大了。如果能够缩短这个跳跃间距，那么学习便不成问题了。可惜的是，论文没有那么多的篇幅给你一步一步地计算。

参考资料

1.周志华，机器学习

2.Ho, Yu-Chi, and David L. Pepyne. "Simple explanation of the no-free-lunch theorem and its implications." Journal of optimization theory and applications 115.3 (2002): 549-570.