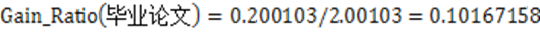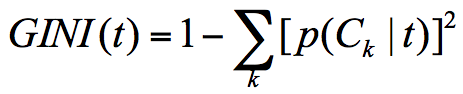决策树原理总结（ID3、C4.5、CART）+ 常见面试问题

系统梳理树类型算法原理加常见面试问题
类容按照决策树、Adaboost、GBDT、XGBoost、LightGBM 顺序进行梳理
本次的重点类容是决策树的CART树

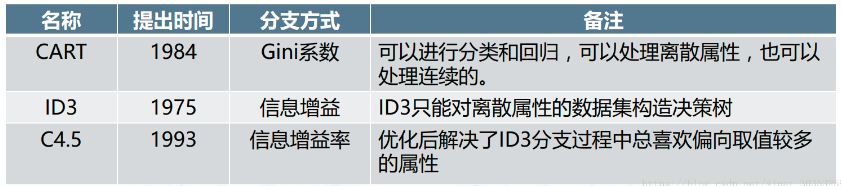
ID3、C4.5介绍请转移到：ID3、C4.5的原理与案例介绍

1. CART树

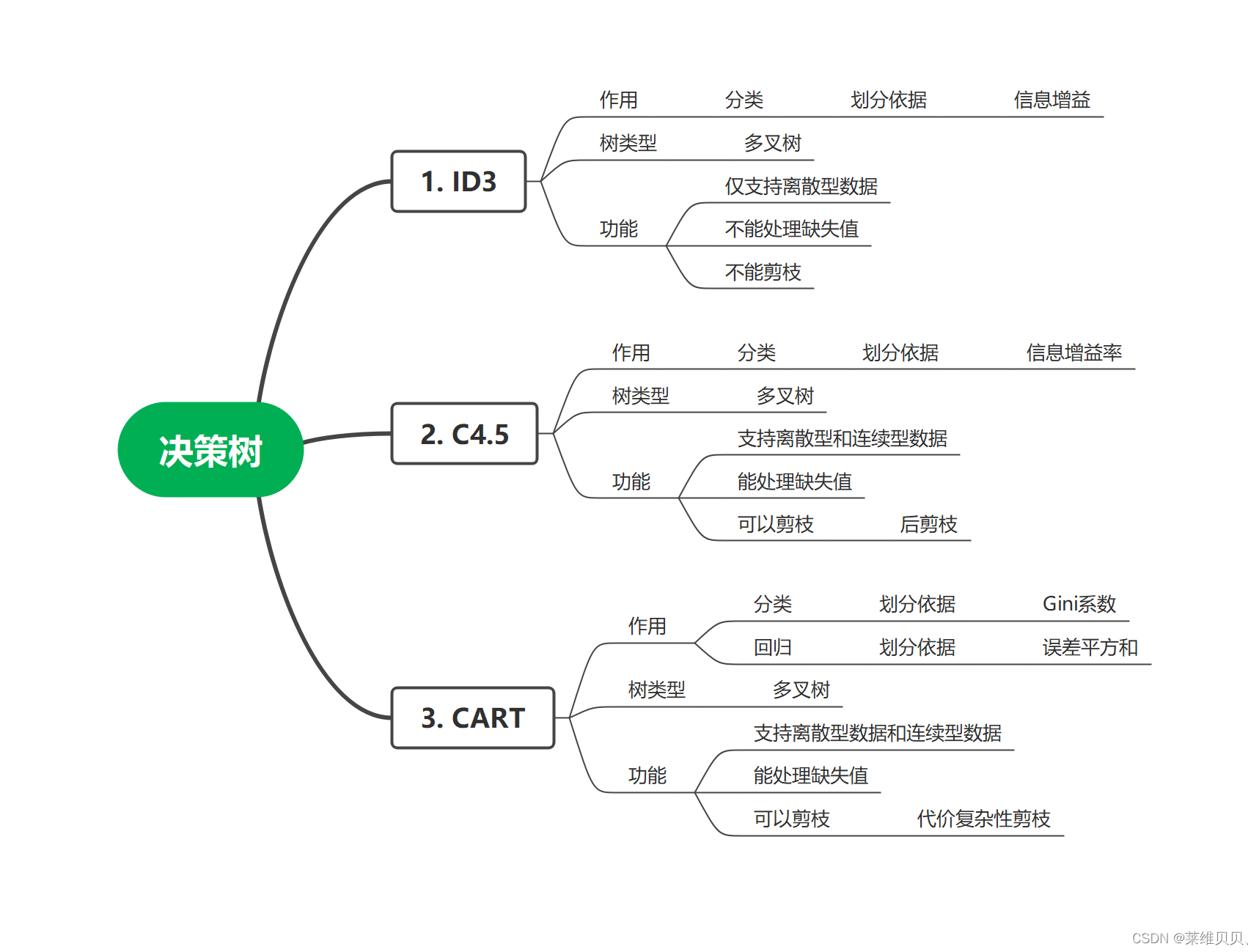
ID3与C4.5虽然可以通过多叉树尽可能的挖掘特征信息，但是随着数据量的增加，其决策树分支也会大量增多。CART算法的二分法简化了决策树的规模，提高了生成决策树的效率。

1.1 CART分类树实现过程

输入： 训练集D，基尼系数的阈值，切分的最少样本个数阈值
第一步： 决策树生成，基于训练数据集生成尽可能大的决策树；
1）假设此时节点的数据集为D，总共有 n 个特征；
2）对第 i （i <= n) 特征进行Gini系数的求解；首先，将 i 特征的数值进行排序(a1,a2,…am)，CART取相邻两样本值的平均数做划分点，一共有m-1个，其中第 i 个划分点Ti表示为：Ti = (ai + ai+1)/2，遍历所有的切分点，小于切分点的数值分到左子树，大于切分点的数值样本分到右子树，计算此时的Cini系数；
3）遍历完所有特征的全部切分点之后，选择Gini系数最小的特征，将数据集D按照此特征的最佳切分点分到左子树和右子树中；
4）对两个子结点递归地调用步骤l~3，直至满足停止条件。
5）算法停止计算的条件是结点中的样本个数小于预定阈值，或样本集的Gini系数小于预定阈值（样本基本属于同一类），或者没有更多特征。
第二步： 决策树剪枝，用验证集对已生成的树进行剪枝并选择最优子树，此时损失函数值最小。

输出： 分类树T

预测：对生成的CART分类树做预测时，假如测试集里的样本落到了某个叶子节点，而该节点里有多个训练样本。则该测试样本的类别为这个叶子节点里概率最大的类别。

1.2 CART分类树案例

假设有K个类，样本点属于第k类的概率为Ck/D(Ck为k类情况下的样本数，D为总样本数），则概率分布的gini指数的定义为：
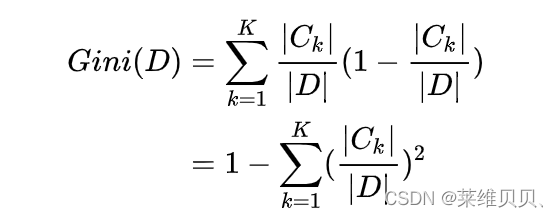
在这里插入图片描述
Gini(D)基尼指数反映了从数据集中随机抽取两个样本，其类别标记不一致的概率。因此基尼指数越小，则数据集纯度越高。

如果样本集合D根据某个特征A被切分点a分割为D1，D2两个部分，那么在特征A的条件下，集合D的gini指数的定义为：
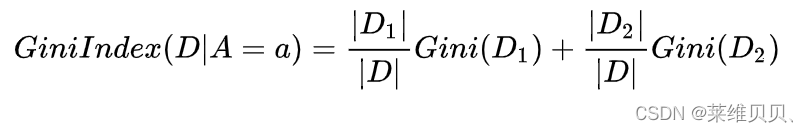
在这里插入图片描述
案列：
**加粗样式**
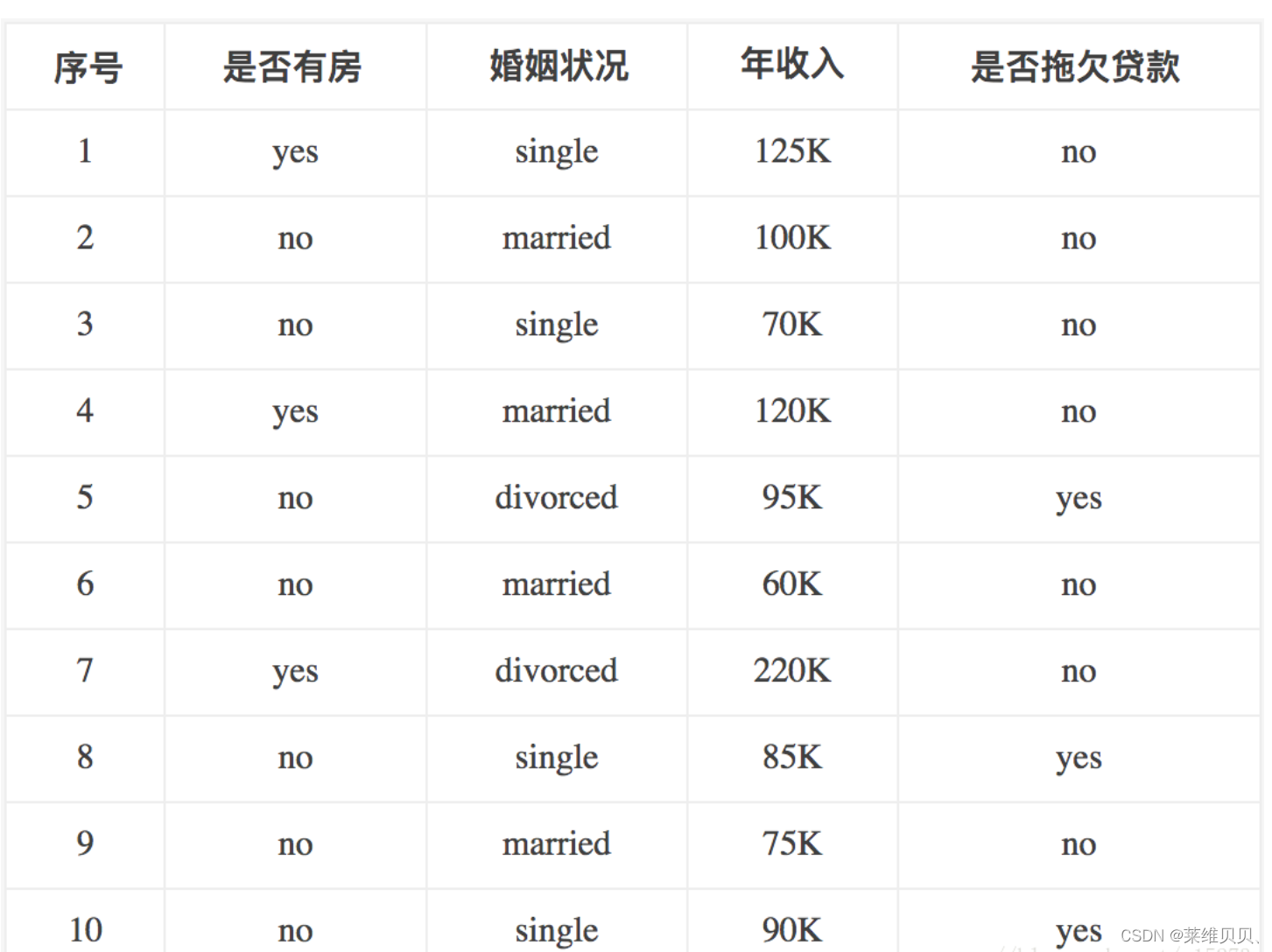
特征：有房情况，婚姻状况和年收入
目标值：是否拖欠贷款

原数据的Gini系数为：

Gini(是否拖欠贷款) = 1−(3/10) ^ 2−(7/10) ^ 2 = 0.42

遍历所有特征，进行Gini系数的计算：
有无房子取值有2种：
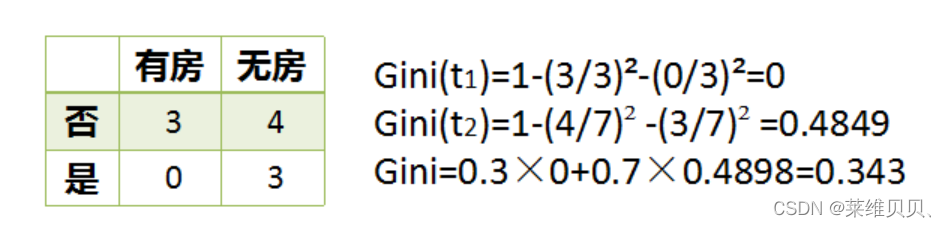
在这里插入图片描述
Ginie增益 = 0.42 - 0.343 = 0.077

婚姻状况取值有3种：
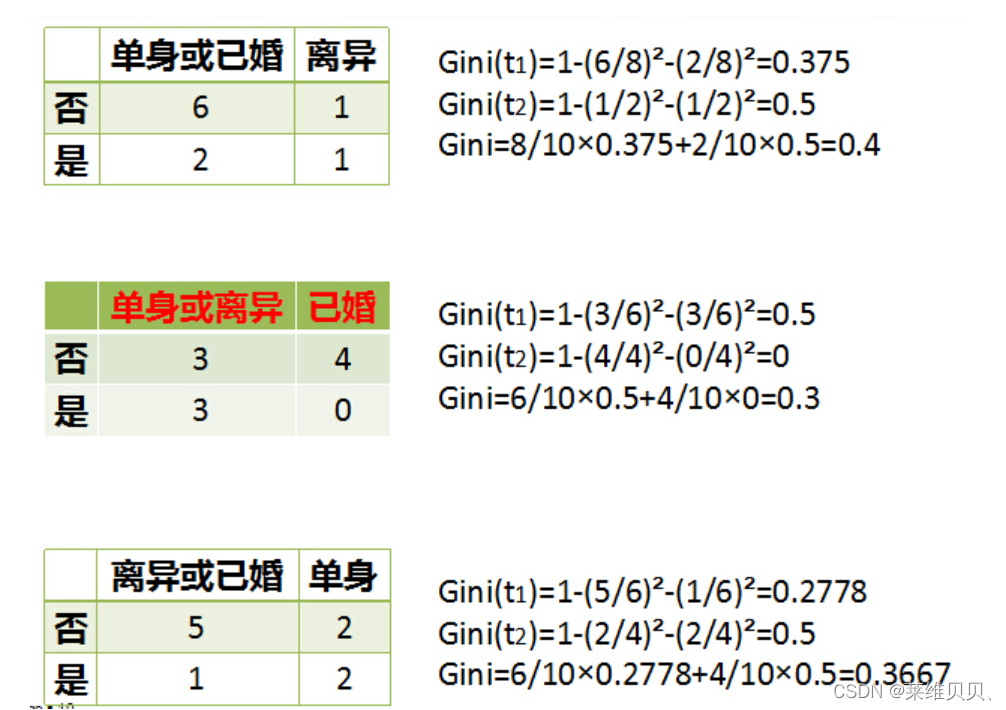
在这里插入图片描述
最佳Gini增益 = 0.42 - 0.3 = 0.12

收入情况是连续值：

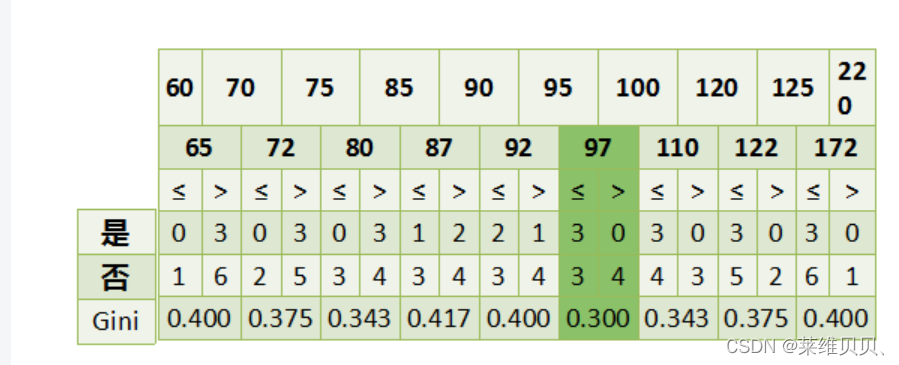
在这里插入图片描述
最佳Gini增益 = 0.42 - 0.3 = 0.12

从上可知，婚姻状况与收入情况的最佳增益都为 0.12，此时取最先进行计算的特征（即婚姻状况）作为数据的划分点。

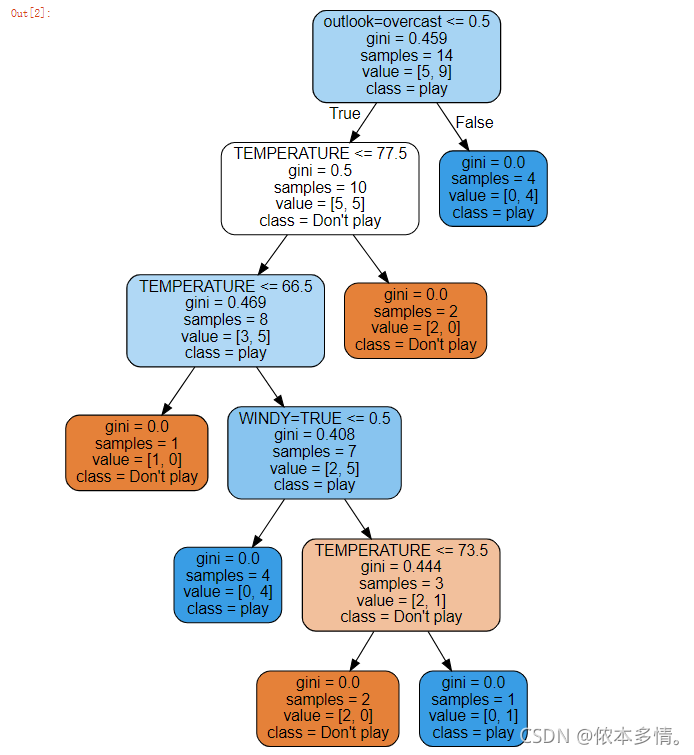
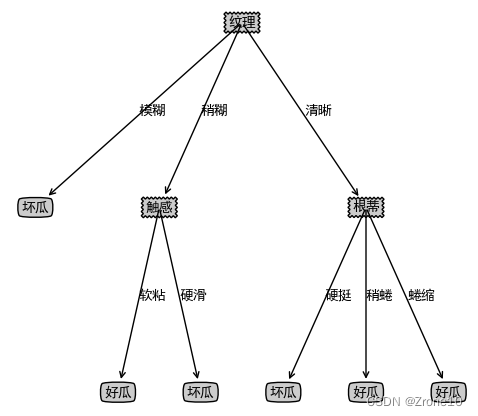
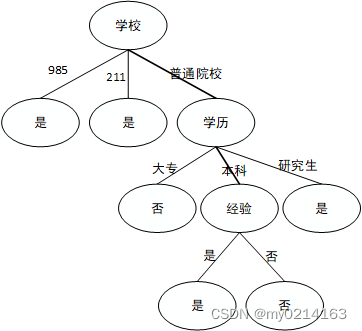
分裂后的数据同上原理进行分裂，最终可以得到以下决策树：
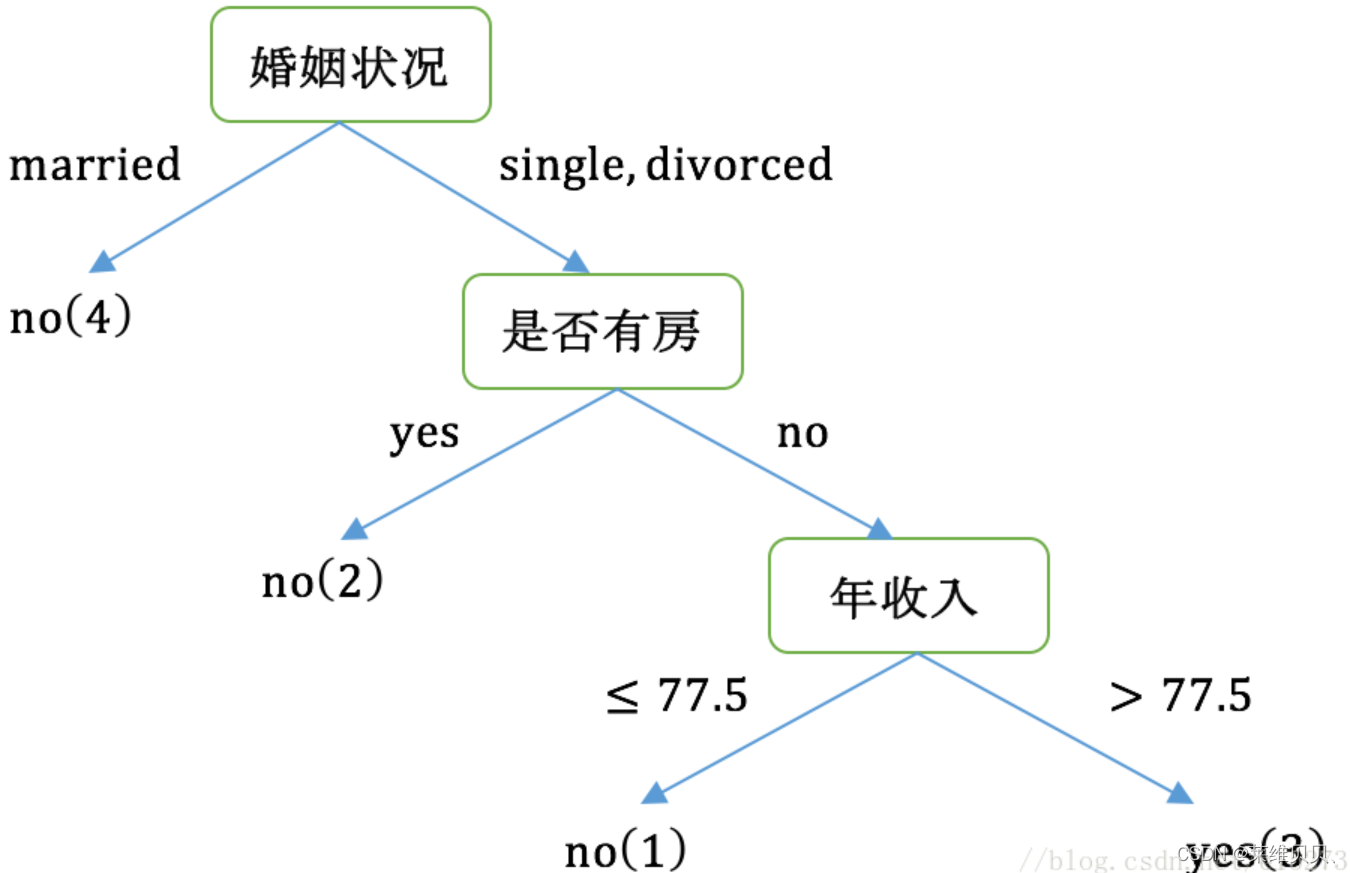
在这里插入图片描述

1.3 剪枝

当分类回归树划分的太细时，噪声数据产生过拟合情况，因此可以通过剪枝来解决。剪枝方法有很多，比如：代价复杂性剪枝、最下误差剪枝、悲观误差剪枝等等。但常用的是代价复杂性剪枝法。
在这里插入图片描述
每个alpha对应一棵树T，alpha是一个动态值；

2. 面试题

1.讲解完成决策树建树过程
答：自上而下，将样本数据依照树的生成分配到对应子树中；每个内部节点表示一个特征，叶子节点表示一个类别。一开始，所有样本积聚在根节点，选择当前最佳的特征，将样本分到不同的子节点，再根据子节点的特征进一步划分，直至所有样本被归到某一个类别中。
2.既然信息增益可以作为划分依据，为什么C4.5还使用信息增益比？
答：当以信息增益作为划分标准时，如果某个特征的取值很多，且根据其对特征进行划分，将会产生很多分支，数据被划分的很细，甚至可以细到一个节点只有一个，这样会导致过拟合。信息增益比，通过对信息增益除以每个特征的固有属性，该属性包括了特征的取值数量，取值越多，固有属性值越大，对其惩罚越大，这样改善了ID3所存在的问题。
3. CART为什么使用基尼系数？
答：基尼系数的意义是：从数据集中随机抽取两个样本，其类别不同的概率，其值越小，则数据集纯度越高。相对于信息增益和信息增益率作为决策指标，基尼指数的运算量比较小，也易于理解，这是cart算法使用基尼指数的主要目的。

4.ID3、ID4.5、CART的异同
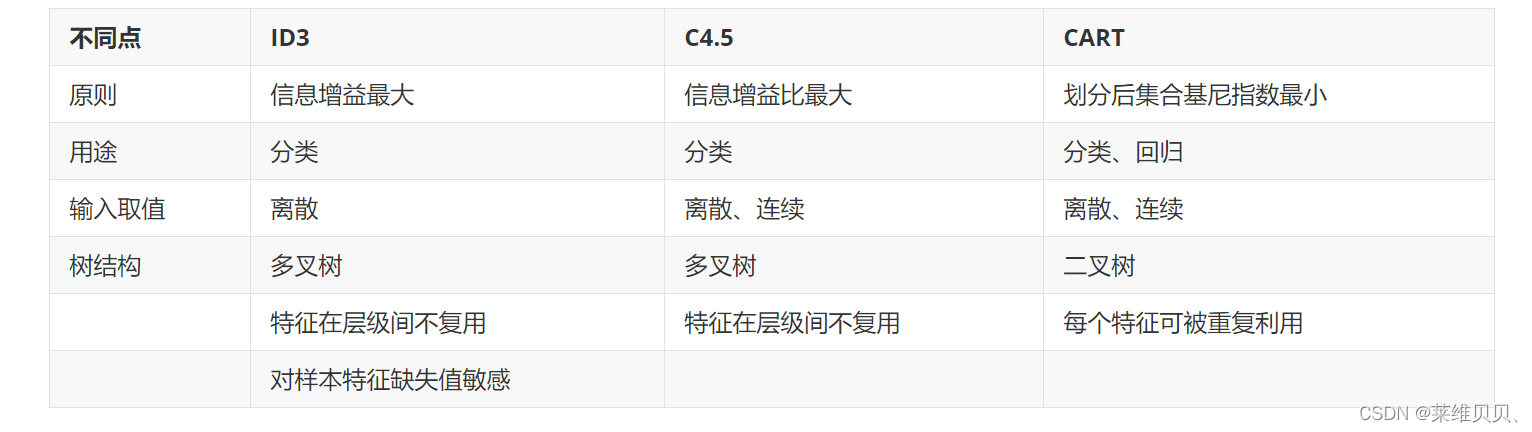
在这里插入图片描述
5.CART做分类和回归的区别是什么？
答：主要两点不同：划分依据不同：分类以基尼系数的大小来度量划分点的优劣情况；回归以方差的大小来度量划分点的优劣情况。预测方式不同：分类取叶子节点概率最大的类别作为预测类别；回归取最终叶子节点的均值或者中位数作为输出值。
6.在分类情况下，CART如何处理离散型和连续性特征？
答：在处理离散型数据和连续性特征的时候，都是首先将按照特征的取值进行排序，再依据相连两个值的平均值将样本分到左子树和右子树中，遍历所有可能，寻找到特征的最佳划分点。
7. 在分类情况下，CART如何处理缺失值？
答：cart使用的是“代理分裂”的方式来对缺失值问题；首先，缺失特征的gini需要乘以非缺失值的比例，如果该缺失值恰好gini增益最大，那么再去遍历剩余的特征，寻找gini增益相近的特征作为代理特征，根据代理特征对样本进行划分。
8. 为什么信息增益偏向取值较多的特征？
答：主要通过公式计算，随着特征取值的增多，样本将会被分的很细，此时的信息熵增益也会随之增加，当样本取值与样本数量相等时，每个样本都被单独分到一个叶子节点中，此时的信息增益最大，但是也造成了过拟合；
9.决策树出现过拟合的原因及解决方法？
答：训练集少，特征多，构造出的决策时比较完美的分类成功，但是这样会把训练集中一些数据的特征当作成整体数据的特点，就是过分的拟合了这些特征，而这些特征并不能代表全部数据，即过拟合了。剪枝防止过拟合，使模型在测试数据上变现良好，更加鲁棒。
10.简单解释一下预剪枝和后剪枝？
答：预剪枝： 控制深度、当前节点数、分裂值对测试集的准确度提升大小来限制树是否继续生长下去；
后剪枝： 生成决策树、自下而上利用交叉验证是否进行剪枝。
11.剪枝过程可以参考哪些参数？
答：可以参考划分之后，c4.5看信息增益率有没有增加，cart看gini增益有没有增加，主要看剪枝前后，模型在验证集上的表现是否得到改善。
12.决策树在做分类的过程中，会对特征进行重复选取吗？
答：cart决策树中特征可以复用，由于cart树在生成树的时候，通过二叉法搜索特征分裂最佳的阈值，在不同的子树下，阈值可能不同，且带来的效益也不同，所以可以通过复用提高模型的预测能力。

参考

https://www.cnblogs.com/wqbin/p/11689709.html
https://blog.csdn.net/e15273/article/details/79648502
https://zhuanlan.zhihu.com/p/139523931
https://zhuanlan.zhihu.com/p/85731206
https://zhuanlan.zhihu.com/p/461032990
https://cloud.tencent.com/developer/article/1486711
https://blog.csdn.net/qq_42722197/article/details/122780760
https://zhuanlan.zhihu.com/p/90825660
https://www.xiaohongshu.com/discovery/item/62778690000000000102d883
http://www.360doc.com/content/22/0415/08/99071_1026582336.shtml