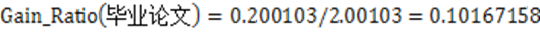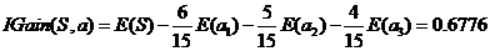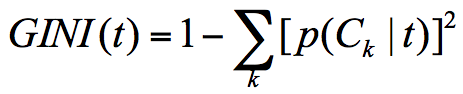决策树实现ID3、C4.5、CART算法
- Author: 浅若清风cyf
- Date: 2020/12/15
一、创建数据集
- 手动
def createDataSet():"""创建测试的数据集:return:"""dataSet = [# 1['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'],# 2['乌黑', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', '好瓜'],# 3['乌黑', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'],# 4['青绿', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', '好瓜'],# 5['浅白', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'],# 6['青绿', '稍蜷', '浊响', '清晰', '稍凹', '软粘', '好瓜'],# 7['乌黑', '稍蜷', '浊响', '稍糊', '稍凹', '软粘', '好瓜'],# 8['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '硬滑', '好瓜'],# ----------------------------------------------------# 9['乌黑', '稍蜷', '沉闷', '稍糊', '稍凹', '硬滑', '坏瓜'],# 10['青绿', '硬挺', '清脆', '清晰', '平坦', '软粘', '坏瓜'],# 11['浅白', '硬挺', '清脆', '模糊', '平坦', '硬滑', '坏瓜'],# 12['浅白', '蜷缩', '浊响', '模糊', '平坦', '软粘', '坏瓜'],# 13['青绿', '稍蜷', '浊响', '稍糊', '凹陷', '硬滑', '坏瓜'],# 14['浅白', '稍蜷', '沉闷', '稍糊', '凹陷', '硬滑', '坏瓜'],# 15['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '软粘', '坏瓜'],# 16['浅白', '蜷缩', '浊响', '模糊', '平坦', '硬滑', '坏瓜'],# 17['青绿', '蜷缩', '沉闷', '稍糊', '稍凹', '硬滑', '坏瓜']]# 特征值列表labels = ['色泽', '根蒂', '敲击', '纹理', '脐部', '触感']# 特征对应的所有可能的情况labels_full = {}for i in range(len(labels)):labelList = [example[i] for example in dataSet]uniqueLabel = set(labelList)labels_full[labels[i]] = uniqueLabelreturn dataSet, labels, labels_full
dataSet, labels, labels_full=createDataSet()
print(dataSet)
print(labels)
print(labels_full)
[['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'], ['乌黑', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', '好瓜'], ['乌黑', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'], ['青绿', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', '好瓜'], ['浅白', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'], ['青绿', '稍蜷', '浊响', '清晰', '稍凹', '软粘', '好瓜'], ['乌黑', '稍蜷', '浊响', '稍糊', '稍凹', '软粘', '好瓜'], ['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '硬滑', '好瓜'], ['乌黑', '稍蜷', '沉闷', '稍糊', '稍凹', '硬滑', '坏瓜'], ['青绿', '硬挺', '清脆', '清晰', '平坦', '软粘', '坏瓜'], ['浅白', '硬挺', '清脆', '模糊', '平坦', '硬滑', '坏瓜'], ['浅白', '蜷缩', '浊响', '模糊', '平坦', '软粘', '坏瓜'], ['青绿', '稍蜷', '浊响', '稍糊', '凹陷', '硬滑', '坏瓜'], ['浅白', '稍蜷', '沉闷', '稍糊', '凹陷', '硬滑', '坏瓜'], ['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '软粘', '坏瓜'], ['浅白', '蜷缩', '浊响', '模糊', '平坦', '硬滑', '坏瓜'], ['青绿', '蜷缩', '沉闷', '稍糊', '稍凹', '硬滑', '坏瓜']]
['色泽', '根蒂', '敲击', '纹理', '脐部', '触感']
{'色泽': {'青绿', '乌黑', '浅白'}, '根蒂': {'硬挺', '蜷缩', '稍蜷'}, '敲击': {'浊响', '清脆', '沉闷'}, '纹理': {'稍糊', '清晰', '模糊'}, '脐部': {'凹陷', '稍凹', '平坦'}, '触感': {'软粘', '硬滑'}}
- 从文件读取
import numpy as np
import pandas as pd
# df=pd.read_excel("./watermelon20.xlsx")
# df.to_csv('./watermelon20.csv',index=False)
df=pd.read_csv('./watermelon20.csv')
print(df)
# 属性集合
attr=df.columns.values.tolist()[1:]
data_org=np.array(df[attr])
# static_attr=df.columns.values.tolist()[1:]#这里的属性 不改变,仅仅作为索引
print(attr)
print(len(attr))
print(data_org.shape)
print(data_org)# print(static_attr) 编号 色泽 根蒂 敲声 纹理 脐部 触感 好瓜
0 1 青绿 蜷缩 浊响 清晰 凹陷 硬滑 是
1 2 乌黑 蜷缩 沉闷 清晰 凹陷 硬滑 是
2 3 乌黑 蜷缩 浊响 清晰 凹陷 硬滑 是
3 4 青绿 蜷缩 沉闷 清晰 凹陷 硬滑 是
4 5 浅白 蜷缩 浊响 清晰 凹陷 硬滑 是
5 6 青绿 稍蜷 浊响 清晰 稍凹 软粘 是
6 7 乌黑 稍蜷 浊响 稍糊 稍凹 软粘 是
7 8 乌黑 稍蜷 浊响 清晰 稍凹 硬滑 是
8 9 乌黑 稍蜷 沉闷 稍糊 稍凹 硬滑 否
9 10 青绿 硬挺 清脆 清晰 平坦 软粘 否
10 11 浅白 硬挺 清脆 模糊 平坦 硬滑 否
11 12 浅白 蜷缩 浊响 模糊 平坦 软粘 否
12 13 青绿 稍蜷 浊响 稍糊 凹陷 硬滑 否
13 14 浅白 稍蜷 沉闷 稍糊 凹陷 硬滑 否
14 15 乌黑 稍蜷 浊响 清晰 稍凹 软粘 否
15 16 浅白 蜷缩 浊响 模糊 平坦 硬滑 否
16 17 青绿 蜷缩 沉闷 稍糊 稍凹 硬滑 否
['色泽', '根蒂', '敲声', '纹理', '脐部', '触感', '好瓜']
7
(17, 7)
[['青绿' '蜷缩' '浊响' '清晰' '凹陷' '硬滑' '是']['乌黑' '蜷缩' '沉闷' '清晰' '凹陷' '硬滑' '是']['乌黑' '蜷缩' '浊响' '清晰' '凹陷' '硬滑' '是']['青绿' '蜷缩' '沉闷' '清晰' '凹陷' '硬滑' '是']['浅白' '蜷缩' '浊响' '清晰' '凹陷' '硬滑' '是']['青绿' '稍蜷' '浊响' '清晰' '稍凹' '软粘' '是']['乌黑' '稍蜷' '浊响' '稍糊' '稍凹' '软粘' '是']['乌黑' '稍蜷' '浊响' '清晰' '稍凹' '硬滑' '是']['乌黑' '稍蜷' '沉闷' '稍糊' '稍凹' '硬滑' '否']['青绿' '硬挺' '清脆' '清晰' '平坦' '软粘' '否']['浅白' '硬挺' '清脆' '模糊' '平坦' '硬滑' '否']['浅白' '蜷缩' '浊响' '模糊' '平坦' '软粘' '否']['青绿' '稍蜷' '浊响' '稍糊' '凹陷' '硬滑' '否']['浅白' '稍蜷' '沉闷' '稍糊' '凹陷' '硬滑' '否']['乌黑' '稍蜷' '浊响' '清晰' '稍凹' '软粘' '否']['浅白' '蜷缩' '浊响' '模糊' '平坦' '硬滑' '否']['青绿' '蜷缩' '沉闷' '稍糊' '稍凹' '硬滑' '否']]
- 决策树结构【ID3】
# 决策树结构:【字典的多重嵌套】
{"纹理": {"稍糊": {"触感": {"硬滑": "否","软粘": "是"}},"清晰": {"根蒂": {"蜷缩": "是","硬挺": "否","稍蜷": {"色泽": {"青绿": "是","浅白": "是","乌黑": {"触感": {"硬滑": "是","软粘": "否"}}}}}},"模糊": "否"}
}
- 决策树结构【C4.5】
{"纹理": {"模糊": "否","稍糊": {"触感": {"软粘": "是","硬滑": "否"}},"清晰": {"触感": {"软粘": {"色泽": {"乌黑": "否","青绿": {"根蒂": {"硬挺": "否","蜷缩": "是","稍蜷": "是"}},"浅白": "否"}},"硬滑": "是"}}}
}
- 决策树结构【CART】
{"清晰": {"yes": {"硬滑": {"yes": "是","no": {"青绿": {"yes": {"稍蜷": {"yes": "是","no": "否"}},"no": "否"}}}},"no": {"乌黑": {"yes": {"浊响": {"yes": "是","no": "否"}},"no": "否"}}}
}
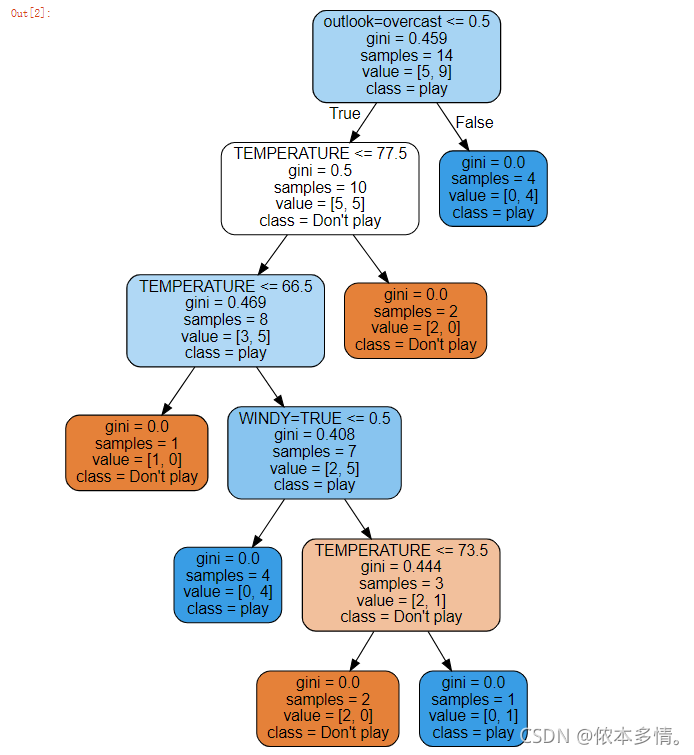
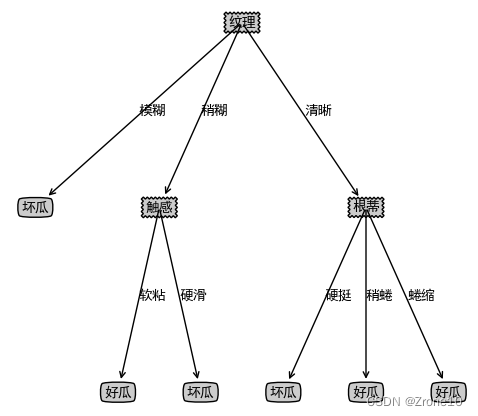
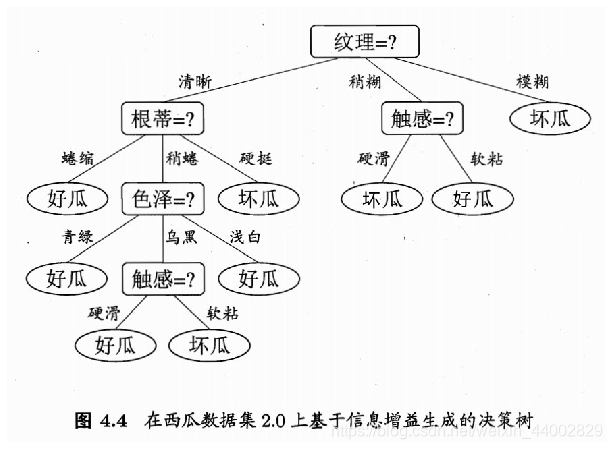
- 可视化结果【ID3】
import matplotlib.pyplot as plt
import numpy as np
fig=plt.figure(figsize=(12,8))
img=plt.imread('./决策树正确结果.jpg')
plt.imshow(img)
plt.axis('off')
plt.show()
- 算法伪代码
fig=plt.figure(figsize=(16,10))
img=plt.imread('./决策树算法流程.jpg')
plt.imshow(np.uint8(img))
plt.axis('off')
plt.show()

- ID3:信息增益
fig=plt.figure(figsize=(16,12))
img=plt.imread('./决策树ID3-信息增益.jpg')
plt.imshow(img)
plt.axis('off')
plt.show()

- C4.5:增益率
fig=plt.figure(figsize=(16,14))
img=plt.imread('./决策树C4.5-增益率.jpg')
plt.imshow(img)
plt.axis('off')
plt.show()

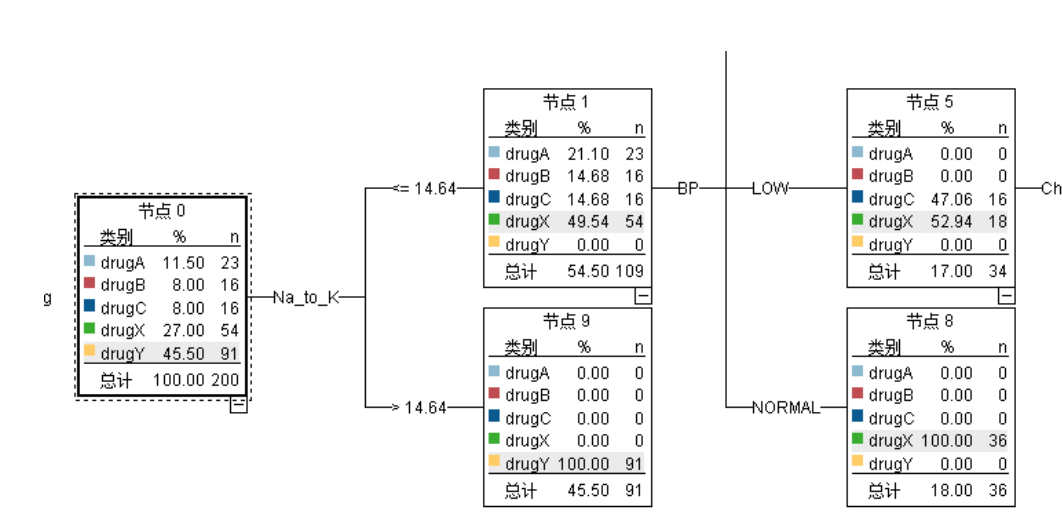
- CART:基尼指数
fig=plt.figure(figsize=(16,12))
img=plt.imread('./决策树CART-基尼指数.jpg')
plt.imshow(img)
plt.axis('off')
plt.show()

- 完整代码
import numpy as np
import pandas as pd
from collections import Counter
import pprint
import jsonclass DecisionTree():D = None # 数据集attribute_list = None # 属性集attribute_value_list = dict() # 属性集对应取值集合tree = None # 决策树【Notice: 字典类型是引用传值,因此需要在init中再初始化它,否则对这个类创建多个对象是该成员变量会指向同一个地址,导致数据会叠加在一起】def __init__(self): # 构造函数:自动加载数据集self.tree=dict()df = pd.read_csv('./watermelon20.csv')# 属性集合self.attribute_list = df.columns.values.tolist()[1:]# 数据集(过滤掉编号)self.D = np.array(df[self.attribute_list])# 获取每个属性的每个属性值for i in range(len(self.attribute_list)):self.attribute_value_list[self.attribute_list[i]] = set(df[self.attribute_list[i]])# 去除类别self.attribute_list = self.attribute_list[:-1]# 判断集合是否属于同一个类别C【是则设为叶结点,标记为类别C】def isSameLabel(self, D):labels = [D[i][-1] for i in range(len(D))] # 取出每个样本的标签return len(set(labels)) == 1 # 属于同一个类别则labels集合元素数量为1,返回True# 判断数据集中的所有属性上的取值是否相同【相同的话设为叶结点,并标记为类别多的类别】def isEmptyOrSameAttribute(self, D, attribute_list):if len(attribute_list) == 0:print("所有属性划分完,无法继续划分,设为叶结点")# print("len(attribute_list) == 0")return Trueelse:attribute_index_list = []for i in attribute_list:attribute_index_list.append(self.attribute_list.index(i))subset_D = D[:, np.array(attribute_index_list)]for i in range(1, subset_D.shape[0]):if (subset_D[0] == subset_D[i]).all():passelse:return Falseprint("所有样本的所有属性相同,无法划分")return True# 计算信息熵def Ent(self, D):labels = D[:, -1]count_result = Counter(labels)# 统计每个标签的频数labels_count = np.array(list(count_result.values()))p = labels_count / D.shape[0]# 计算信息熵ent = -1 * np.sum(p * np.log2(p))return ent# 计算信息增益def Gain(self, D, attribute):# 统计属性attribute的每个取值的样本数attribute_values = np.squeeze(D[:, self.attribute_list.index(attribute)]) # 获取每个样本在属性attribute上的取值attribute_keys = np.array(list(set(list(attribute_values)))) # 获取所有属性值D_split = []for i in range(attribute_keys.shape[0]):mask = (attribute_values == attribute_keys[i])D_split.append(D[mask]) # 按照属性 attribute每个取值划分数据集D_split = np.array(D_split)# 计算每个属性值的信息熵ent_list = []attribute_i_count_list = []for i in range(D_split.shape[0]):ent_list.append(self.Ent(D_split[i]))attribute_i_count_list.append(D_split[i].shape[0])ent_list = np.array(ent_list)attribute_i_count_list = np.array(attribute_i_count_list)# 计算信息增益gain = self.Ent(D) - np.sum(attribute_i_count_list / D.shape[0] * ent_list)return gain# 计算增益率def Gain_ratio(self, D, attribute):D_attribute_values = np.squeeze(D[:, self.attribute_list.index(attribute)]) # 获取每个样本在属性attribute上的取值count_result=Counter(D_attribute_values)attribute_i_count_list=np.array(list(count_result.values()))IV=-1*np.sum(attribute_i_count_list/D.shape[0]*np.log2(attribute_i_count_list/D.shape[0]))gain_ratio=self.Gain(D,attribute)/IVreturn gain_ratio# 计算基尼值【数据集D的不纯度】def Gini(self,D):# 获取集合D的标签D_labels=D[:, -1]count_result = Counter(D_labels)# 统计每个标签的频数labels_count = np.array(list(count_result.values()))p = labels_count / D.shape[0]return 1-np.sum(p*p)# 计算基尼指数【计算属性attribute中按照某个属性划分得到的两个集合(二叉树)的基尼系数最小的作为划分属性】def Gini_index(self,D,attribute):# 获取样本集D在属性attribute上的取值D_attribute_values = np.squeeze(D[:, self.attribute_list.index(attribute)]) # 获取每个样本在属性attribute上的取值# 统计每个属性值的样本数【字典】count_result=Counter(D_attribute_values)# 统计属性的所有取值【转换成数组】attribute_keys=np.array(list(count_result.keys()))
# attribute_values_count_list=np.array(list(count_result.values()))# 按照不同属性值划分数据集【是/否】【CART算法是划分为二叉树,而不是多叉树】gini_index_list=[]for i in range(attribute_keys.shape[0]):D_split=[]D_split_count=[]mask = (D_attribute_values == attribute_keys[i])D_split.append(D[mask]) # 取值与属性值相同:是D_split.append(D[(1-mask).astype('bool')]) D_split = np.array(D_split)D_split_count.append(D_split[0].shape[0])D_split_count.append(D_split[1].shape[0])D_split_count=np.array(D_split_count)# 计算按照该属性值划分后的Gini值gini_list=[]for i in range(D_split.shape[0]):gini_list.append(self.Gini(D_split[i]))gini_list = np.array(gini_list)# 计算基尼指数gini_index = np.sum(D_split_count / D.shape[0] * gini_list) # D.shape[0]==2gini_index_list.append(gini_index)# 选择最小的基尼指数作为属性attribute的基尼指数gini_index_list=np.array(gini_index_list)gini_index_min=np.min(gini_index_list)gini_index_min_attribute_value=attribute_keys[np.argmin(gini_index_list)]return gini_index_min,gini_index_min_attribute_value# 计算最优划分属性def get_bestAttribute(self, D, attribute_list, alg='ID3'):'''Notice: ID3和C4.5算法执行次函数有一个返回值,而CART算法有两个返回值'''if alg == 'ID3':best = attribute_list[0]max_gain = 0for i in attribute_list:gain_i = self.Gain(D, i)if gain_i > max_gain:best = imax_gain = gain_i# print('best=', best, 'max_gain=', max_gain)return bestelif alg == 'C4.5':# 增益率准则对可取值数目较少的属性有所偏好,C4.5算法并不是直接选择增益率最大的候选划分属性,# 而是使用一个启发式:先从候选划分属性中找出信息增益高于平均水平的属性,再从中选择增益率最高的gain_list=[]for i in attribute_list:gain_list.append(self.Gain(D,i))gain_list=np.array(gain_list)gain_mean=np.mean(gain_list)attribute_chosen=np.array(attribute_list)[gain_list>=gain_mean] # 注意要加=,当只有一个属性值或者所有属性增益率相同时,没有属性的增益率大于平均值gain_rate_list=[]for i in attribute_chosen:gain_rate_list.append(self.Gain_ratio(D,i))gain_rate_list=np.array(gain_rate_list)best = attribute_chosen[np.argmax(gain_rate_list)]return bestelif alg=='CART':# 基尼值Gini(D)反映了从数据集D中随机抽取两个样本,其类别标记不一致的概率,因此,Gini(D)值越小,数据集D的纯度越高# 在属性集中选择划分后基尼指数最小的属性作为最优属性gini_index_list=[]gini_index_attribute_value_list=[]for i in attribute_list:gini_index_min,gini_index_min_attribute_value=self.Gini_index(D,i)gini_index_list.append(gini_index_min)gini_index_attribute_value_list.append(gini_index_min_attribute_value)gini_index_list=np.array(gini_index_list)gini_index_attribute_value_list=np.array(gini_index_attribute_value_list)best_attribute_idx=np.argmin(gini_index_list)return attribute_list[best_attribute_idx],gini_index_attribute_value_list[best_attribute_idx]else:raise Exception("请选择合法的划分属性选优算法!")# 构建决策树tree【这里树结构采用嵌套的字典类型】def createTree(self, tree, D, attributes,alg='ID3'):attribute_list = attributes.copy()# 判断数据集是否属于同一个类别【不用再划分】if self.isSameLabel(D):return D[0][-1]if self.isEmptyOrSameAttribute(D, attribute_list):# 获取样本数多的类labels = D[:, -1] # 获取所有样本的标签labels_set = set(list(np.squeeze(labels))) # 获取标签集合labels_dict = dict() # 获取每个标签对应的样本for i in labels_set: # 初始化labels_dict[i] = 0for i in range(D.shape[0]): # 统计每个标签的样本数labels_dict[D[i][-1]] += 1keys = list(labels_dict.keys())values = list(labels_dict.values())return keys[np.argmax(values)]if alg=='ID3' or alg=='C4.5':# 选择最优划分属性【选择后需要在属性集中取出该属性再进行递归】best_attribute = self.get_bestAttribute(D, attribute_list, alg=alg)# 属性集取出最优属性,进行下一轮递归attribute_list.remove(best_attribute)# 获取数据集在最优属性上的所有取值attribute_values = self.attribute_value_list[best_attribute] # 按照最优属性的每个值划分数据集D_attribute_values = np.squeeze(D[:, self.attribute_list.index(best_attribute)]) # 获取每个样本在属性attribute上的取值D_split = dict()# 按每个取值划分数据集for i in attribute_values:mask = (D_attribute_values == i)D_split[i] = D[mask] # 按照属性 attribute每个取值划分数据集# 对最优属性的每个取值进行遍历subTree = dict()tree[best_attribute] = dict()for i in attribute_values:if D_split[i].shape[0] == 0: # 该属性上没有样本,根据父结点的样本分布作为当前结点的样本分布labels=D[:,-1]result=Counter(labels)result_keys=list(result.keys())result_values=list(result.values())label=result_keys[np.argmax(result_values)]subTree[i]=labelcontinuesubTree[i] = self.createTree(tree[best_attribute], D_split[i], attribute_list,alg=alg)tree[best_attribute] = subTreenode=dict() # 需要单独创建一个结点,而不能直接返回subTree或tree,会导致子节点为Nonenode[best_attribute]=subTreereturn node # 当某个属性值还需划分时,返回子树,否则该属性值的value为Noneelif alg=='CART':# 选择最优划分属性和最优属性值【CART算法与ID3和C4.5不同,CART算法使用属性值按是否相等划分成二叉树】best_attribute,best_attribute_value = self.get_bestAttribute(D, attribute_list, alg=alg)# CART算法的属性可以重复使用
# attribute_list.remove(best_attribute)# 获取数据集在最优属性上的所有取值
# attribute_values = self.attribute_value_list[best_attribute] # 按照最优属性值划分成两个子数据集D_attribute_values = np.squeeze(D[:, self.attribute_list.index(best_attribute)]) # 获取每个样本在属性attribute上的取值D_split = dict()# 按照最优属性值划分数据集mask = (D_attribute_values == best_attribute_value)D_split['yes'] = D[mask] D_split['no'] = D[(1-mask).astype('bool')]# 对最优属性的每个取值进行遍历subTree = dict()tree[best_attribute_value] = dict()attribute_values=['yes','no']for i in attribute_values: subTree[i] = self.createTree(tree[best_attribute_value], D_split[i], attribute_list,alg=alg)tree[best_attribute_value] = subTreenode=dict() # 需要单独创建一个结点,而不能直接返回subTree或tree,会导致子节点为Nonenode[best_attribute_value]=subTreereturn node # 当某个属性值还需划分时,返回子树,否则该属性值的value为None# 构建决策树def build(self,alg='ID3'):self.createTree(self.tree, self.D, self.attribute_list,alg=alg)# 可视化决策树【递归输出】def show(self,tree,blank):if type(tree)!=type(self.tree):returnkeys=list(tree.keys())for i in keys:for t in range(blank):print('\t', end='')print('{',i,':')self.show(tree[i],blank+1)if type(tree[i])!=type(self.tree): # 是否为叶结点for t in range(blank + 1):print('\t', end='')print(tree[i])for t in range(blank):print('\t', end='')print('}')# 可视化决策树【调包pprint】def showTreeDict(self):pprint.pprint(self.tree)# 可视化决策树【调包json】 def showTreeDictJson(self):js=json.dumps(self.tree,indent=8,ensure_ascii=False)print(js)# 使用ID3/C4.5生成的决策树进行判断def decision(self,sample):print("输入样本:",sample)attribute=list(self.tree.keys())[0] # '纹理'tree=self.treewhile True:if type(tree)==type(self.tree):tree = tree[attribute]tree=tree[sample[self.attribute_list.index(attribute)]]if type(tree)==type(self.tree):attribute=list(tree.keys())[0]else:print("识别结果:",end='')print('好瓜') if tree=='是' else print("坏瓜")break# 使用CART生成的决策树进行判断def decision_CART(self,sample):print("输入样本:",sample)attribute=list(self.tree.keys())[0] # '纹理'tree=self.treewhile True:if type(tree)==type(self.tree):# 获取树的keyattribute_value=list(tree.keys())[0]# 检索对应的属性attribute_idx=-1attribute_value_set=set()attribute_value_set.add(attribute_value)for i in self.attribute_list:if attribute_value_set.issubset(self.attribute_value_list[i]):attribute_idx=self.attribute_list.index(i)print(i)breakif attribute_idx==-1:raise Exception("Can't find the attribute of {}".format(attribute_value))# 判断样本该属性值是否与决策树的属性值相等attribute_value_equal=(attribute_value==sample[attribute_idx])tree=tree[attribute_value]if attribute_value_equal:tree=tree['yes']else:tree=tree['no']else:print("识别结果:",end='')print('好瓜') if tree=='是' else print("坏瓜")breakdt=DecisionTree()
dt.build(alg='ID3')
dt.showTreeDictJson()
dt.decision(dt.D[0][:-1])
{"纹理": {"模糊": "否","稍糊": {"触感": {"软粘": "是","硬滑": "否"}},"清晰": {"根蒂": {"硬挺": "否","蜷缩": "是","稍蜷": {"色泽": {"乌黑": {"触感": {"软粘": "否","硬滑": "是"}},"青绿": "是","浅白": "是"}}}}}
}
输入样本: ['青绿' '蜷缩' '浊响' '清晰' '凹陷' '硬滑']
识别结果:好瓜
dt=DecisionTree()
dt.build(alg='C4.5')
dt.showTreeDictJson()
dt.decision(dt.D[0][:-1])
{"纹理": {"模糊": "否","稍糊": {"触感": {"软粘": "是","硬滑": "否"}},"清晰": {"触感": {"软粘": {"色泽": {"乌黑": "否","青绿": {"根蒂": {"硬挺": "否","蜷缩": "是","稍蜷": "是"}},"浅白": "否"}},"硬滑": "是"}}}
}
输入样本: ['青绿' '蜷缩' '浊响' '清晰' '凹陷' '硬滑']
识别结果:好瓜
dt=DecisionTree()
dt.build(alg='CART')
# pprint.pprint(dt.tree)
# dt.show(dt.tree,0)
dt.showTreeDictJson()
dt.decision_CART(dt.D[0][:-1])
{"清晰": {"yes": {"硬滑": {"yes": "是","no": {"青绿": {"yes": {"稍蜷": {"yes": "是","no": "否"}},"no": "否"}}}},"no": {"乌黑": {"yes": {"浊响": {"yes": "是","no": "否"}},"no": "否"}}}
}
输入样本: ['青绿' '蜷缩' '浊响' '清晰' '凹陷' '硬滑']
纹理
触感
识别结果:好瓜
谨以此纪念《数据挖掘与机器学习》课程期末考试手算ID3决策树!o(╥﹏╥)o ——2021.1.21