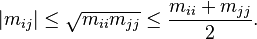正定矩阵、负定矩阵、半正定矩阵、半负定矩阵
载▼
1.正定矩阵
一个 n×n 的实 对称矩阵 M 是 正定 的, 当且仅当 对于所有的非零实系数 向量 z ,都有 zTMz > 0 。其中 z T 表示 z 的 转置 。 2.负定矩阵
与正定矩阵相对应的,一个n×n的埃尔米特矩阵 是负定矩阵当且仅当对所有不为零的
是负定矩阵当且仅当对所有不为零的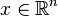 (或
(或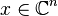 ),都有:
),都有:

3.半正定矩阵
 是半正定矩阵当且仅当对所有不为零的
是半正定矩阵当且仅当对所有不为零的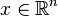 (或
(或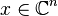 ),都有:
),都有:
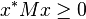
4.半负定矩阵
 是半负定矩阵当且仅当对所有不为零的
是半负定矩阵当且仅当对所有不为零的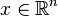 (或
(或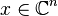 ),都有:
),都有:
正定阵的判别[编辑]
对n×n的埃尔米特矩阵M,下列性质与“M为正定矩阵”等价:
| 1. | 矩阵 的所有的特征值 的所有的特征值 都是正的。根据谱定理,M必然与一个实对角矩阵D相似(也就是说 都是正的。根据谱定理,M必然与一个实对角矩阵D相似(也就是说 ,其中P是幺正矩阵,或者说M在某 ,其中P是幺正矩阵,或者说M在某个正交基可以表示为一个实对角矩阵)。因此,M是正定阵当且仅当相应的D的对角线上元素都是正的。 |
| 2. | 半双线性形式 定义了一个Cn上的内积。实际上,所有Cn上的内积都可看做由某个正定阵通过此种方式得到。 |
| 3. | M是n个线性无关的k维向量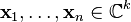 的Gram矩阵,其中的k为某个正整数。更精确地说,M定义为: 的Gram矩阵,其中的k为某个正整数。更精确地说,M定义为: 换句话说,M具有 |
| 4. | M的所有顺序主子式,也就是顺序主子阵的行列式都是正的(西尔维斯特准则)。明确来说,就是考察下列矩阵的行列式:
对于半正定矩阵来说,相应的条件应改为所有的主子式非负。顺序主子式非负并不能推出矩阵是半正定的。比如以下例子: |
| 5. | 存在唯一的下三角矩阵 ,其主对角线上的元素全是正的,使得: ,其主对角线上的元素全是正的,使得:
其中 |
对于实对称矩阵,只需将上述性质中的 改为
改为 ,将“共轭转置”改为“转置”就可以了。
,将“共轭转置”改为“转置”就可以了。
相关性质[编辑]
若 为半正定阵,可以写作
为半正定阵,可以写作 。如果
。如果 是正定阵,可以写作
是正定阵,可以写作 。这个记法来自泛函分析,其中的正定阵定义了正算子。
。这个记法来自泛函分析,其中的正定阵定义了正算子。
对于一般的埃尔米特矩阵, 、
、 ,
,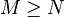 当且仅当
当且仅当 。这样可以定义一个在埃尔米特矩阵集合上的偏序关系。类似地,可以定义
。这样可以定义一个在埃尔米特矩阵集合上的偏序关系。类似地,可以定义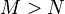 。
。
| 1. | 每个正定阵都是可逆的,它的逆也是正定阵。如果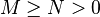 那么 那么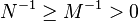 。 。 |
| 2. | 如果 是正定阵, 是正定阵,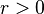 为正实数,那么 为正实数,那么 也是正定阵。 也是正定阵。如果 |
| 3. | 如果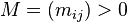 那么主对角线上的系数 那么主对角线上的系数 为正实数。于是有 为正实数。于是有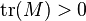 。此外还有 。此外还有 |
| 4. | 矩阵 是正定阵当且仅当存在唯一的正定阵 是正定阵当且仅当存在唯一的正定阵 使得 使得 。根据其唯一性可以记作 。根据其唯一性可以记作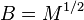 ,称 ,称 为 为 的平方根。对半正定阵也有类似结论。同时,如果 的平方根。对半正定阵也有类似结论。同时,如果 那么 那么 . . |
| 5. | 如果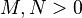 那么 那么 ,其中 ,其中 表示克罗内克乘积。 表示克罗内克乘积。 |
| 6. | 对矩阵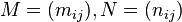 ,将两者同一位置上的系数相乘所得的矩阵记为 ,将两者同一位置上的系数相乘所得的矩阵记为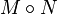 ,即 ,即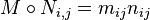 ,称为 ,称为 与 与 的阿达马乘积。如果 的阿达马乘积。如果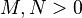 ,那么 ,那么 。如果 。如果 为实系数矩阵,则有如下不等式成立: 为实系数矩阵,则有如下不等式成立:
|
| 7. | 设 , , 为埃尔米特矩阵。如果 为埃尔米特矩阵。如果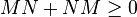 ( ( ),那么 ),那么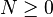 ( (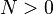 )。 )。 |
| 8. | 如果 为实系数矩阵,则 为实系数矩阵,则 。 。 |
| 9. | 如果 为实系数矩阵,那么存在 为实系数矩阵,那么存在 使得 使得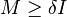 ,其中 ,其中 为单位矩阵。 为单位矩阵。 |
from:
http://zh.wikipedia.org/wiki/正定矩阵
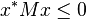

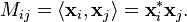
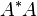 的形式,其中A不一定是方阵,但需要是单射的。
的形式,其中A不一定是方阵,但需要是单射的。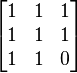
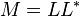 .
. 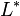 是
是 、乘积
、乘积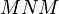 与
与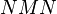 都是正定的。如果
都是正定的。如果 ,那么
,那么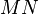 仍是正定阵。
仍是正定阵。