如何定义一个微服务架构？通常情况下，定义应用程序架构分三步。但是，世界上并没有一个机械化的流程可以遵守，然后指望这个流程输出一个合理的架构。这里只能介绍一个笼统的方法，现实世界中，这是一个不断迭代和持续创新的过程。跟所有的软件开发一样，定义架构是一项艺术而非技术。
一开始我们需要拿到领域专家或现有应用的需求文档，定义应用架构的第一步则是将应用的需求提炼为各种关键请求。可以使用系统操作(System Operation)来描述这些请求。系统操作是应用必须处理的请求的一种抽象描述。它既可以是更新数据的命令，也可以是检索数据的查询。第二步是确定如何分解服务。有几种策略可供选择。一种源于业务架构学派的策略是定义与业务能力相对应的服务。另一种策略是围绕软件驱动设计的子域来分解和设计服务。但这些策略的最终结果都是围绕业务概念而非技术概念分解和设计服务。第三步是确定每个服务的API。为此，架构师需将第一步标识的每个系统操作分配给服务。服务可以完全独立地实现操作。或者，它可能需要多个服务协作。在这种情况下，可以确定服务的协作方式，这通常需要服务来支持其他操作。
由于需求通常由领域专家或现有需求给出，所以微服务架构架构师的主要职责是第二步(确定如何分解服务)和第三步(确定每个服务的API)。由于第三步依赖第二步，所以对架构师来说，服务拆分是微服务架构落地的关键。然后如何将系统操作划分到各个服务中，并定义服务API。

服务拆分标准

服务拆分有几个障碍需要克服。首先是网络延迟。由于服务之间的网络往返可能太多，特定的分解是不切实际的。分解的另一个障碍是服务之间的同步通信降低了整个应用的可用性。第三个障碍是需要维护跨服务的数据一致性。第四个障碍就是上帝类(God Class)问题。它广泛存在整个应用中。
软件开发领域追求松耦合和高内聚，微服务开发也不例外，在进行服务拆分时，尽量保证服务自身高度内聚，服务间松散耦合。松耦合和高内聚这两个概念在不同的上下文中使用，如面向对象编程中，这里先讨论着两个概念在微服务中的含义。

松耦合

如果做了服务之间的松耦合，那么修改一个服务就不需要修改另一个服务。使用微服务最重要的一点是，能够独立修改及部署单个服务而不需修改系统的其他部分。
对于紧耦合方式做服务之间的集成，会导致一个服务的修改使其消费者同步修改，这与微服务概念不符。一个松耦合的服务，应该尽可能少地知道与之协作的那些服务的信息。这也意味着，应该限制两个服务之间不同调用形式的数量，因为除了潜在的性能问题之外，过度的通信可能会导致紧耦合。
服务之间的交互采用API完成，这样做就封装了服务的实现细节。这允许服务在不影响客户端的情况下，对实现方式作出修改。松耦合服务是改善开发效率、提升可维护性和可测试性的关键。小的、松耦合的服务更容易被理解、修改和测试。
服务通过API来实现服务间调用，这样就避免了外界对服务的数据库的直接访问和调用。服务自身持久化数据就如同类的私有属性一样，是不对外的。保证数据的私有属性是实现松耦合的前提之一。这样做，就允许开发者修改服务的数据结构，而不同提前与其他服务的开发者相互协商。这样做在运行时也实现了更好的隔离。例如，一个服务的数据库加锁不会影响另外的服务。

高内聚

高内聚就是将相关的行为聚集在一起，把不相关的行为放到别处。这样做的话，如果改变某个行为的话，可以只在一个地方修改，然后尽快的发布。如果需要在多个不同的地方做修改，那么可能就需要同时发布多个微服务才能交付这个功能。在多个不同的地方进行修改会很慢，同时部署多个服务风险也很高，这两者都是要极力避免的。所以，找到问题的边界就可以确保相关的行为能放在同一个地方，并且它们会和其他边界以尽量松耦合的形式进行通信。

服务拆分实现

微服务架构的关键是如何进行功能分解，也就是说如何将一个大型的应用构建为一组服务。在进行拆分前，再次声明下微服务理解上的误区。微服务这个术语的一个问题是让开发者将关注点错误的聚焦在微上。它暗示服务应该非常小。其他基于大小的术语也是如此。实际上，大小不是一个重要的考虑因素。更好的目标是将精心设计的服务定义为能力由小团队开发的服务，并且交付时间最短，与其他团队协作最少。理论上，团队可能值负责单一服务，因此服务绝不是微小的。相反，如果服务需要大型团队或需要很长时间进行测试，那么拆分团队或服务可能是有意义的。另外，如果因为其他服务的变更而不断需要同步更新自己团队负责的服务，或者所需负责服务正在触发其他服务的同步更新，那么这表明服务没有实现松耦合。这表明构建的可能是一个分布式的单体应用。
和定义微服务架构一样，服务拆分也不是一个机械化的流程。相反，有多种拆分策略可供选择。每一种都是从一个侧面来解决问题，并且使用它们独有的一些术语。这里重点介绍两种服务拆分策略，一种是根据业务能力进行服务拆分，另一种是根据领域驱动设计进行服务拆分。

业务拆分

创建微服务架构的策略之一就是根据业务能力进行服务拆分。业务能力是一个来自于业务架构建模的术语。业务能力是指一些能够为公司(或组织)产生价值的商业活动。如在线商店的业务能力包括：商品管理、购物车管理、订单管理、库存管理、发货、退货等。
组织的业务能力通常是指这个组织的业务是做什么，它们通常是稳定的。与之相反，组织采用何种方式来实现它的业务能力，是随着时间不断变化的。如数字化推动了商业流程的线上化、自动化。如之前购物，需要到线下实体店购买，而随着互联网的兴起，在线购物已经成为主流。虽然，购物的形式发生了很大的变化，但是购物这项业务并没有变化。
一个组织拥有哪些业务能力，是通过对组织的目标、结构和商业流程的分析得来的。每一个业务能力都可被认为是一个服务，除非它是面向技术的而非面向业务的。这里以餐馆系统为例，介绍下如何基于业务拆分服务。常见的餐馆系统有如下能力：
(1) 餐馆菜单和其他信息管理，如营业地址和时间。
(2) 消费者管理，消费者相关信息管理。
(3) 订单获取和履行。(a) 消费者创建和管理订单。(b) 餐馆管理订单的生产过程。© 送餐。
(4) 会计记账。(a）管理跟消费者相关的记账。(b) 管理跟餐馆相关的记账。
(5) 其他能力。
确定了业务能力后，接下来就可以为每个能力或相关能力组定义服务，也即将业务能力映射到服务。决定将哪个级别的能力层次结构映射到服务是一个非常主观的判断。这里进行如下划分：
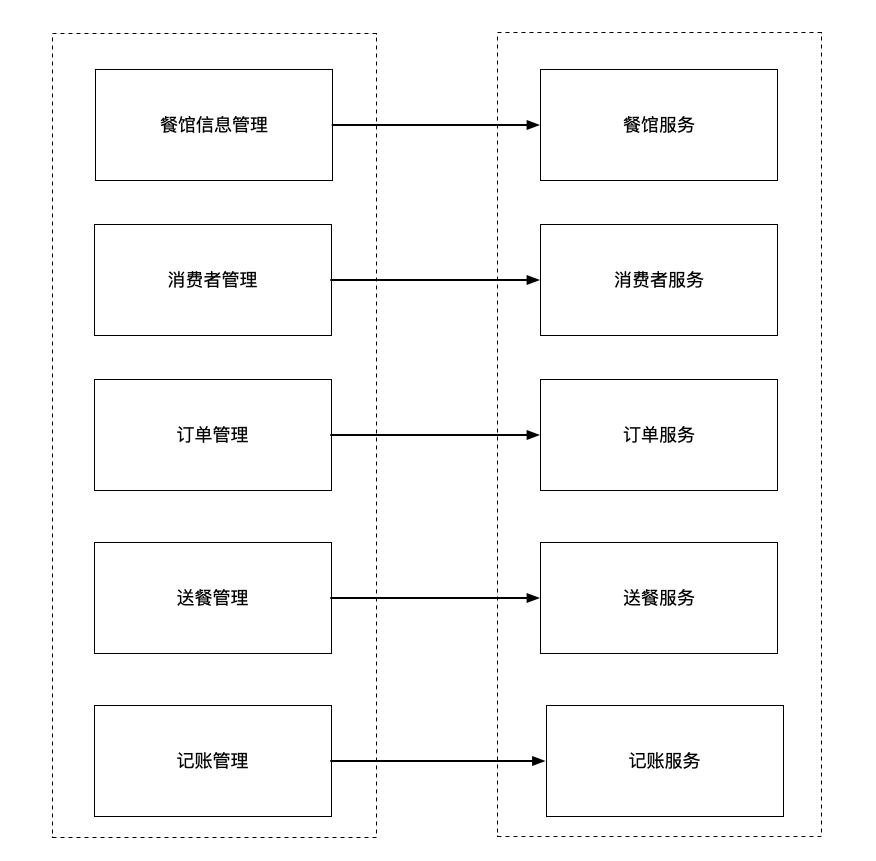
请添加图片描述
在上面的服务，将一个业务能力映射为一个服务，在实际的划分中，也存在将多个业务能力划分到一个服务的场景。
围绕能力组织服务的一个关键好处是，因为业务能力是稳定的，所以最终的架构也相对稳定。架构的各个组件可能会随着业务的具体实现方式的变化而发展，但架构仍保持不变。但是，随着时间的推移，可能部分功能因为过多的进程间通信而导致特定的分解效率低下，导致需要将这些服务合并在一起。相反，服务可能会在复杂性方面增长到值的将其拆分为多个服务的程度。所以，服务拆分不是一次性工作，应随着领域认知的加深，按需进行服务合并或服务拆分。

DDD拆分

Eric Evans 提出的领域驱动设计是构建复杂软件的方法论，这些软件通常都以面向对象和领域模型为核心。领域模型以解决具体问题的方式包含了一个领域内的知识。领域模型会被紧密地映射到应用的设计和实现环节。在微服务架构的设计层面，DDD有两个特别重要的概念，子域和限界上下文。
传统的企业架构建模会为整个企业建立一个单独的模型，在这样的模型中，会有适用于整个应用全局的业务实体定义，这类传统建模方式的挑战在于，让组织内的所有团队都对全局单一的建模和术语定义达成一致是困难的。另外，对于组织中的特定团队而言，这个单一的业务实体定义可能过于复杂，超出了他们的需求。DDD则定义多个领域模型，且每个模型都有明确的范围。
领域驱动为每一个子域定义单独的领域模型，子域是领域的一部分，领域是DDD中用来描述应用问题域的一个术语。识别子域的方式跟识别业务能力一样：分析业务并识别业务的不同专业领域，分析产出的子域定义结果也会跟业务能力非常接近。
DDD把领域模型的边界称为限界上下文(Bounded Context)。限界上下文包括实现这个模型的代码集合。当使用微服务架构时，每一个限界上下文对应一个或一组服务。换言之，通过DDD的方式定义子域，并把子域对应为一个服务，这样就完成了服务拆分的工作。基于业务拆分的实例餐馆系统的领域划分如下：
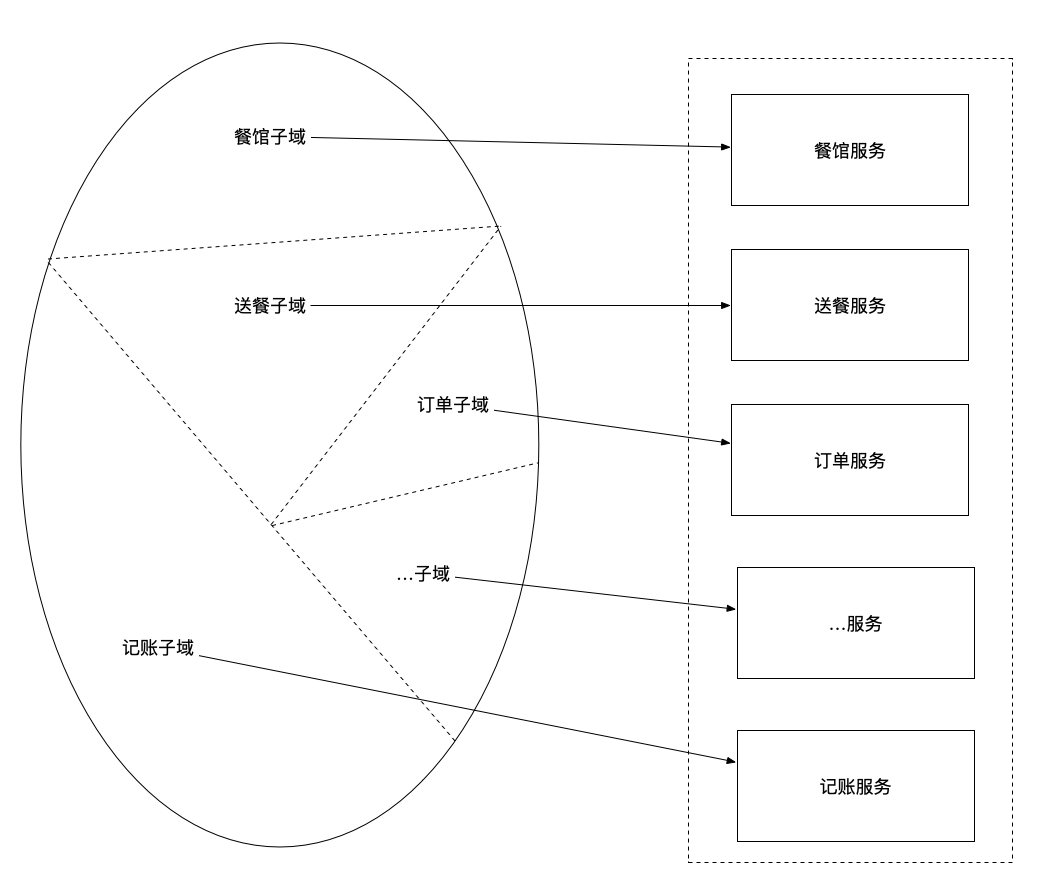
请添加图片描述
DDD和微服务架构十分契合。DDD的子域和限界上下文的概念，可以很好地跟微服务架构中的服务进行匹配。而且，微服务架构中的自治团队负责服务开发的理念，也跟DDD中每个领域模型由一个独立团队负责开发的理念吻合。另外，子域用于它自己的领域模型这个概念，为消除上帝类和优化服务拆分提供了方法。