目录

1 高斯核

1.1 一维定义

1.2 二维定义

1.2.1 应用高斯核的过程

1.2.2 不同σ值的高斯核情况

1.2.3 不同核宽度情况

1.2.4 高斯核（滤波）特性

1.2.5 使用高斯核做平滑滤波相对箱式滤波的优点

2 噪声 和 滤波

2.1 椒盐噪声、脉冲噪声

2.1.1 形成原因

2.1.2 滤波方法

2.1.3 效果

2.2 高斯噪声

2.2.1 形成原因

2.2.2 滤波方法

2.2.3 效果

---

1 高斯核

高斯核在图像处理中有广泛应用（后续很多其他大章节的算子中会用到高斯核），高斯核就是用一个正态分布去给核中元素赋值。

1.1 一维定义

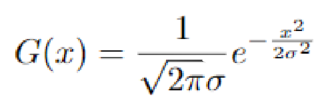
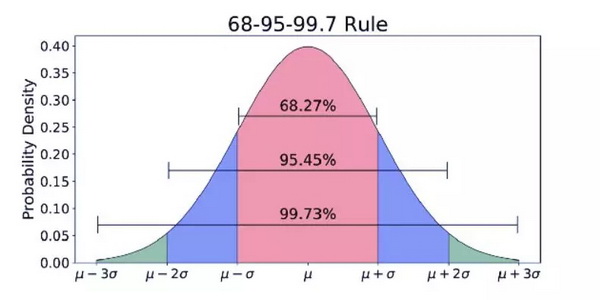
68% 的数据在±1 个标准差(σ)内;

95% 的数据在±2 个标准差(σ)内;

99.7% 的数据在±3 个标准差(σ)内。

1.2 二维定义

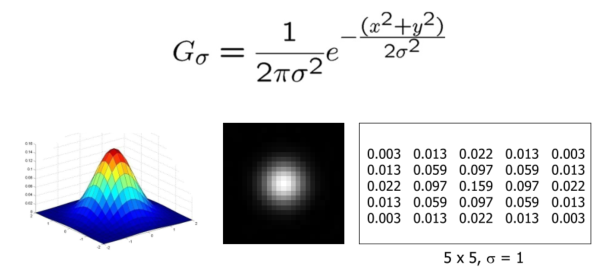
1.2.1 应用高斯核的过程

1. 指定σ值
2. 在指定σ值后，还要对整个核进行归一化（核内所有元素值和为1，这是为了确保高斯核作用于图像上后，新图的能量（也就是亮度）大小不变）

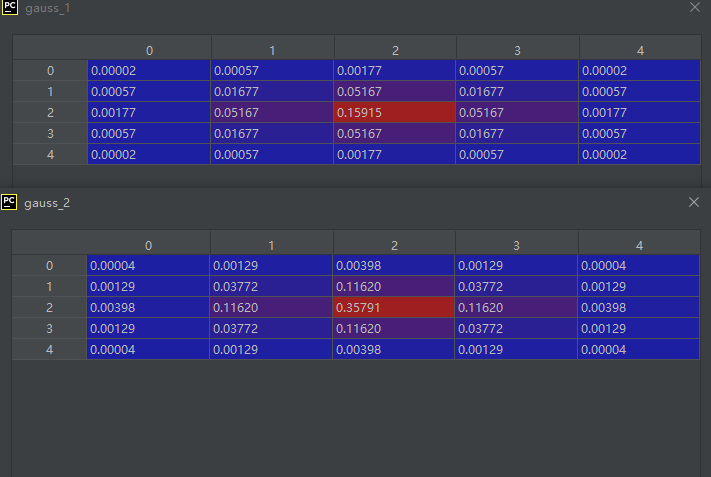
1.2.2 不同σ值的高斯核情况

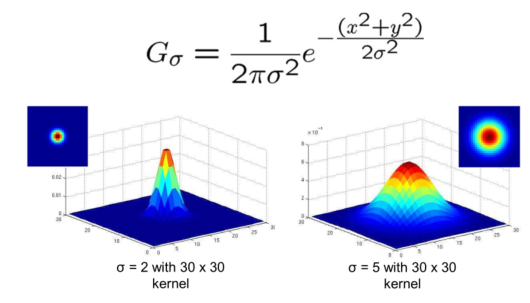
1.2.3 不同核宽度情况

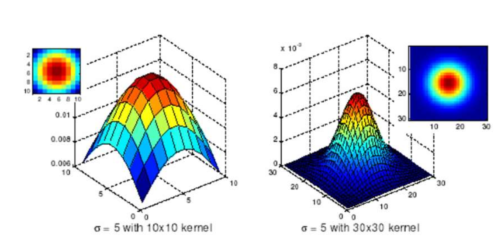
指定σ，高斯核宽度基本也可以算出来：按照3σ原则（该区域内元素值累加超达到全体元素值累计的99.7%），当σ=1时，产生作用的核宽度基本是1+2*(3*1)=7像素；当σ=3时，产生作用的核宽度是1+2*(3*3)=19像素。

为什么？因为超过一定宽度后的元素值基本都接近0了，当你用高斯核对图像进行处理时，高斯核中心区之外的这些位置几乎就不产生什么作用了。下图是不同σ下，元素值和距中心点距离之间的关系。

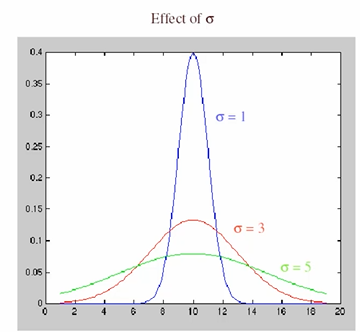
1.2.4 高斯核（滤波）特性

1. 去噪时，能把高频信号去掉（低通滤波器）（相当于图像平滑）。
2. 确定了σ，高斯核宽度也就确定。
3. 一个大高斯核，能够用两个小高斯核连续操作实现，从而减少计算量（证明见专题1）。（因为卷积有这种性质）
4. 高斯核能分解

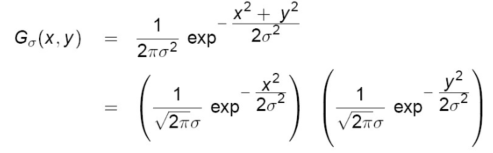
1.2.5 使用高斯核做平滑滤波相对箱式滤波的优点

在《专题1——卷积和互相关》中，提到普通的箱式平滑滤波如下：

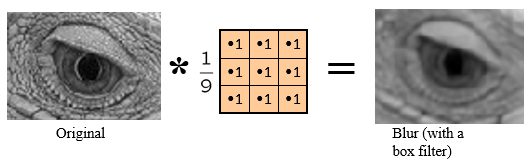
滤波核是一个正方形，新图中每个像素点值用原图中一块矩形区域相似累加平均得到，这么做会引发一点点问题，导致新图上产生横竖一样的痕迹纹路。如果把滤波核换成各方向中心对称的高斯核，则没有这个问题。两者效果对比如下（右下角图采用的高斯核进行平滑滤波）：

2 噪声 和 滤波

2.1 椒盐噪声、脉冲噪声

有孤立的纯黑、 纯白的像素点

2.1.1 形成原因

像素感应器失效、通讯受干扰等。

2.1.2 滤波方法

中值滤波——取临近像素的中值作为替换。

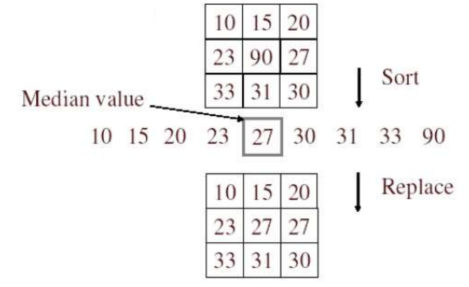
2.1.3 效果

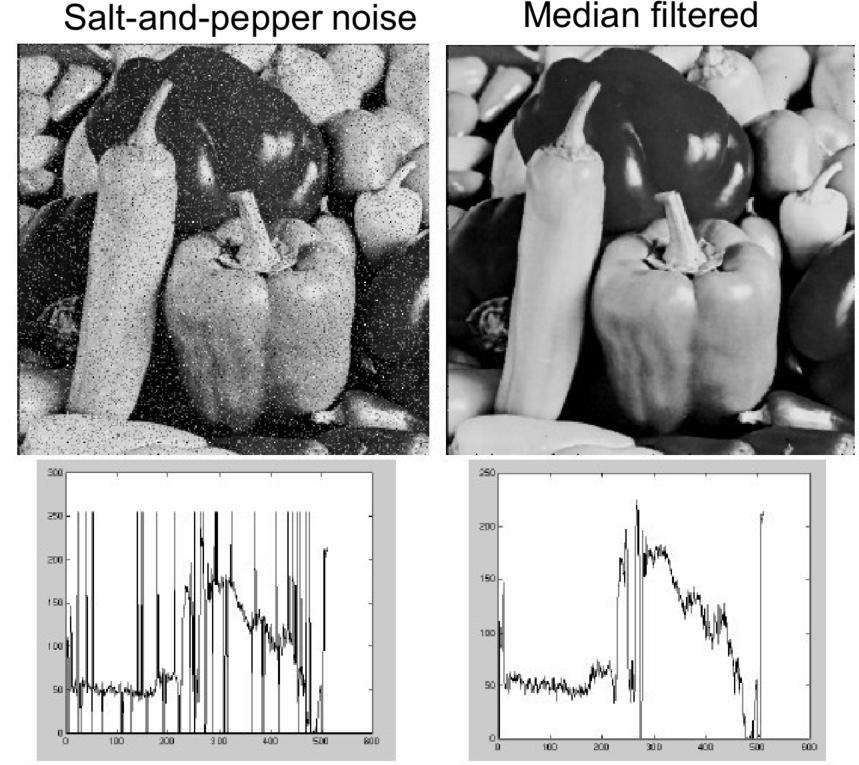
2.2 高斯噪声

各种灰度值噪声都有，成正态分布。

2.2.1 形成原因

传感器亮度不均匀、各种其他噪声叠加等。

2.2.2 滤波方法

因为高斯噪声的范围遍布所有灰度级，所以，任何一种低通、高通、带通滤波器都无法完全将其滤除，我们只能尽可能的获得较好效果。滤除高斯噪声的主要方法有：平滑线性滤波、高斯滤波、维纳滤波还有小波去噪

2.2.3 效果