支持向量机
- 支持向量:支持平面把两类类别划分开的超平面的向量点
- 机:一种算法
- SVM 是一种二分类模型
- 线性可分支持向量机:通过硬间隔最大化,学习一个线性分类器
- 线性支持向量机:通过软间隔最大化,学习一个线性分类器
- 非线性支持向量机:通过核技巧,学习一个非线性分类器
线性可分支持向量机
几何间隔
函数间隔
见 :Python机器学习笔记:SVM(2)——SVM核函数 - 知乎 (zhihu.com)
拉格朗日乘子法
第一种情况:最小值在可行区域内
g ( x ∗ ) < 0 ∇ x f ( x ∗ ) = 0 g(x^*)<0 \\ \nabla _x f(x^*) =0 g(x∗)<0∇xf(x∗)=0
第二种情况:最小值在可行区域外
g ( x ∗ ) = 0 − ∇ x f ( x ∗ ) = α ∇ x g ( x ∗ ) α > 0 g(x^*)=0 \\ -\nabla _x f(x^*) = \alpha \nabla_x g(x^*) \\ \alpha>0 g(x∗)=0−∇xf(x∗)=α∇xg(x∗)α>0
著名的KKT条件,整合了上面两种情况的条件
∇ x L ( x ∗ , α ∗ ) = 0 α ∗ > 0 α ∗ g ( x ∗ ) = 0 g ( x ∗ ) ≤ 0 \nabla_xL(x^*, \alpha ^*)=0 \\ \alpha ^*>0\\ \alpha^*g(x^*)=0 \\g(x^*) \le 0 ∇xL(x∗,α∗)=0α∗>0α∗g(x∗)=0g(x∗)≤0
SVM目标函数求解
- 目标函数:
min w , b 1 2 ∣ ∣ w ∣ ∣ 2 s.t. 1 − y ( i ) ( w ⋅ x ( i ) + b ) ≤ 0 , i = 1 , 2 , … , m \min _{w, b} \frac 1 2||w||^2 \\ \text { s.t. }\quad 1-y^{(i)}\left(w \cdot x^{(i)}+b\right) \leq 0, \quad \mathrm{i}=1,2, \ldots, \mathrm{m} w,bmin21∣∣w∣∣2 s.t. 1−y(i)(w⋅x(i)+b)≤0,i=1,2,…,m
- 构造拉格朗日函数:
L ( w , b , α ) = 1 2 ∥ w ∥ 2 − ∑ i = 1 m α ( i ) y ( i ) ( w ⋅ x ( i ) + b ) + ∑ i = 1 m α ( i ) L(w, b, \alpha)=\frac{1}{2}\|w\|^{2}-\sum_{i=1}^{m} \alpha^{(i)} y^{(i)}\left(w \cdot x^{(i)}+b\right)+\sum_{i=1}^{m} \alpha^{(i)} L(w,b,α)=21∥w∥2−i=1∑mα(i)y(i)(w⋅x(i)+b)+i=1∑mα(i)
- 根据拉格朗日对偶性,原始问题的对偶问题是极大极小问题:
原 始 问 题 : min w , b max α L ( w , b , α ) 对 偶 问 题 : max α min w , b L ( w , b , α ) 原始问题:\qquad \qquad \min _{w, b} \max _{\alpha} L(w, b, \alpha) \\ 对偶问题:\qquad \qquad \max _ \alpha \min _{w,b} L(w, b, \alpha) 原始问题:w,bminαmaxL(w,b,α)对偶问题:αmaxw,bminL(w,b,α)
线性支持向量机
非线性支持向量机
核技巧
原空间: x = ( x 1 , x 2 ) T x=(x_1,x_2)^T x=(x1,x2)T
新空间: z = ( z 1 , z 2 ) T z=(z_1,z_2)^T z=(z1,z2)T
设原空间到新空间的变换 z = ϕ ( x ) = ( x 1 2 + x 2 2 ) T z=\phi (x) =(x_1^2+x_2^2)^T z=ϕ(x)=(x12+x22)T
则把原空间中的椭圆 w 1 x 1 2 + w 2 x 2 2 + b = 0 w_1x_1^2+w_2 x_2^2+b=0 w1x12+w2x22+b=0 变换为新空间中的直线 w 1 z 1 + w 2 z 2 + b = 0 w_1z_1+w_2 z_2+b=0 w1z1+w2z2+b=0
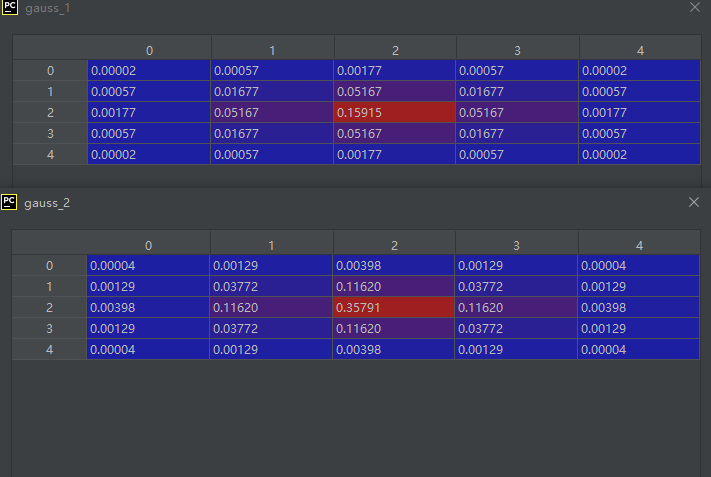
高斯核公式:
k ( x , z ) = exp ( − ∥ x − z ∥ 2 2 σ 2 ) k(x, z)=\exp \left(-\frac{\|x-z\|^{2}}{2 \sigma^{2}}\right) k(x,z)=exp(−2σ2∥x−z∥2)
def gauss_kernel(x,z,delta):m,n = np.shape(x)k = np.mat(np.zeros((m,1)))for i in range(m):delta_row=x[i,:] - zk[i] = delta_row * delta_row.Tk = np.exp(k/(-2*delta)**2)return k
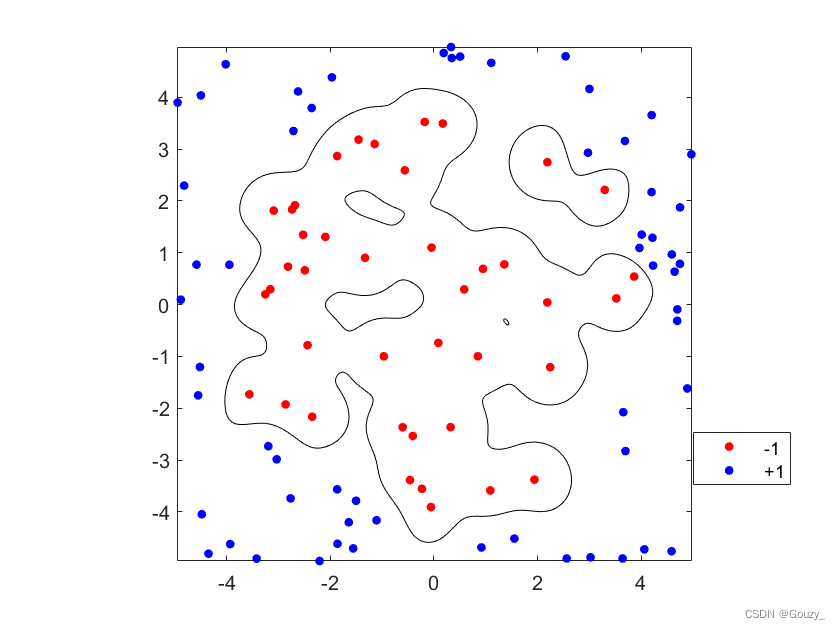
数值实验
在平面 R 2 R^2 R2 上取矩形 I = [ − 5 , 5 ] × [ − 5 , 5 ] I=[-5,5] \times [-5,5] I=[−5,5]×[−5,5] ,并在 I I I 中随机产生100个样本点,作为训练样本点,得到训练样本集 Ω = { ( x i , y i ) ∣ i = 1 , 2 , . . . , 100 } ⊂ I × { − 1 , + 1 } \Omega =\{(x_i,y_i)|i=1,2,...,100 \} \subset I \times \{-1,+1 \} Ω={(xi,yi)∣i=1,2,...,100}⊂I×{−1,+1} ,其中,如果 x i x_i xi 落在圆 t 1 2 + t 2 2 = 16 ( ( t 1 , t 2 ) ) ∈ R 2 t^2_1+t^2_2=16 ((t_1,t_2)) \in \bf R^2 t12+t22=16((t1,t2))∈R2内,则取 y i = − 1 y_i=-1 yi=−1 , 否则取 y i = + 1 y_i=+1 yi=+1
采用Gauss支撑向量机进行学习。Gauss核函数的参数选取及其分类效果,见表4.4.1.学习后的得到的分类曲线见图4.4.1
| 高斯核中的 σ 的值 | 100个训练样本中SV的个数 | 300个实验样本被误分的个数 |
|---|---|---|
| 0.1 | 99 | 205 |
| 0.5 | 64 | 103 |
| 20.0 | 37 | 48 |
| 26.0 | 52 | 24 |
| 28.0 | 56 | 14 |
| 29.0 | 55 | 9 |
| 30.0 | 60 | 8 |
| 50.0 | 62 | 52 |
| 200.0 | 63 | 53 |