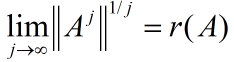一、范数、条件数与谱半径

1. 范数

1.1 向量范数

向量范数的具体形式可以有很多种(满足上述三个条件的)，但常用的有以下三种

$设向量x={\left({\xi }_1,{\xi }_2,\dots ,{\xi }_n\right)}^T\in C^n,$
$(1)\Vert x{\Vert }_1={\sum }_{i=1}^n|{\xi }_i|$ 1范数
$(2)\Vert x{\Vert }_2={\left({{\sum }_{i=1}^n|{\xi }_i|}^2\right)}^{\frac{1}{2}}$ 2范数
$(3)\Vert \mathbf{x}{\Vert }_{\infty }={\max }_{1\le i\le n}\left|{\mathbf{\xi }}_i\right|$ $\infty$范数
上述三种范数可统一地表示为 p 范数, 即 $\Vert x{\Vert }_p={\left({\sum }_{i=1}^n{\left|{\mathbf{x}}_i\right|}^p\right)}^{\frac{1}{p}}$
$其中p=1,2时很清楚,而\Vert {x|}_{\infty }={\lim }_{p\to +\infty }\Vert x{\Vert }_p$

1.2 矩阵范数

算子范数

–由向量范数诱导的矩阵范数

设$\Vert \cdot \Vert$ 是Cⁿ上的向量范数, 定义 C^nxn 上的函数为矩阵A的m范数

$\Vert A{\Vert }_m$=${\max }_{|x|=1}\Vert Ax\Vert ,A\in C^{n\times n}$

其中由向量1,2，$\infty$范数诱导的矩阵范数$\Vert A{\Vert }_1，\Vert A{\Vert }_2，\Vert A{\Vert }_{\infty }$

$(1)\Vert A{\Vert }_1={\max }_{\mid \Vert x{\Vert }_1=1}\Vert Ax{\Vert }_1={\max }_{1\le j\le n}{\sum }_{i=1}^n\left|a_{ij}\right|,$ L1诱导范数，极大列和
$(2)\Vert A{\Vert }_{\infty }={\max }_{|x{|}_{\infty }=1}\Vert Ax{\Vert }_{\infty }={\max }_{1\le i\le n}{\sum }_{j=1}^n\left|a_{ij}\right|,$L无穷诱导范数，极大行和
$(3)\Vert A{\Vert }_2={\max }_{|x{|}_2=1}\Vert Ax{\Vert }_2=\sqrt{{\lambda }_{\max }}，{\lambda }_{\max }是A^{H}A$ 的最大特征值 L2诱导范数，谱半径

矩阵范数

$(1)\Vert A{\Vert }_{m_1}={\sum }_{i=1}^n{\sum }_{j=1}^n|a_{ij}|$ ， m1 范数
$(2)\Vert \mathbf{A}{\Vert }_{m_{\infty }}=n{\max }_{1\le i,j\le n}{a}_{ij}\mid$， m无穷范数
$(3)\Vert A{\Vert }_F=\sqrt{{\sum }_{i=1}^n{\sum }_{j=1}^n{\left|a_{ij}\right|}^2}=\sqrt{\mathrm{tr}\left(A^{H}A\right)}=\sqrt{\mathrm{tr}\left(A{A}^H\right)}$， F范数

例题

2. 谱半径ρ(A) 是矩阵A特征值模的最大值

• 谱半径小于1，矩阵序列{Ak}收敛；
• 谱半径是矩阵范数的下界 ，即 ||A||>= max(λi) = ρ(A)

3. 矩阵条件数

• 判断矩阵病态与否的一种度量，条件数越大矩阵越病态。对应矩阵的3种范数，相应地可以定义3种条件数： 函数 $con{d}_1(A)、cond{(}_2(A)以及con{d}_{\infty }(A)$
• 病态：对于线性方程组Ax=b，如果A的条件数大，b的微小改变就能引起解x较大的改变，数值稳定性差。如果A的条件数小，b有微小的改变，x的改变也很微小，数值稳定性好
• cond(A) = ||A|| * ||A^-1||

定理：扰动误差，给矩阵A以扰动δA；其中x是Ax= b的唯一解，x̅是（A+δA)x = b的唯一解，有如下不等式`

例题