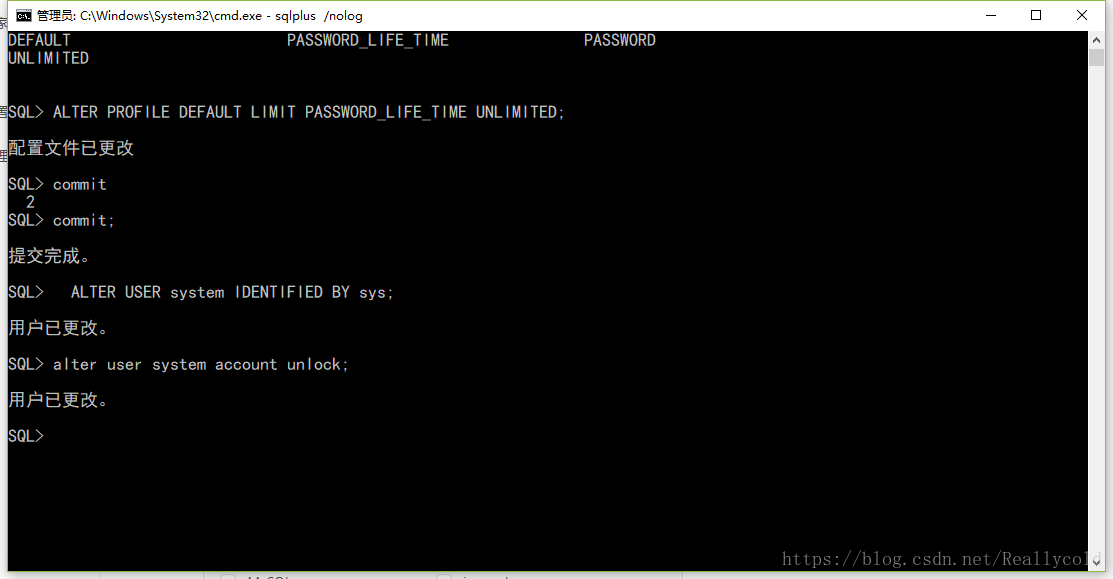
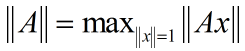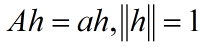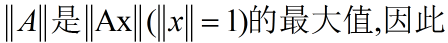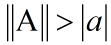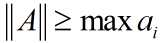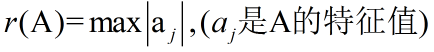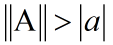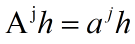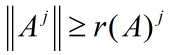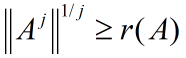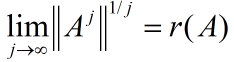本节介绍复欧几里得空间映射到其自身的矩阵.给出其范数的一个简单而有用的下界.

该矩阵范数的定义同实欧几里得空间.

0 说明：

本节以下的研究都是针对复欧几里得空间到自身的映射

1 范数

2 特征值

设A为任意的复方阵.h为A的一个长度为1的特征向量.a为对应的特征值.

则：

由于：

该式对任意特征值成立,于是有：

其中ai取遍A的全体特征值.

3 谱半径

设A为某线性空间到其自身的线性映射,A的谱半径(Spectral radius)

r(A)定义为：

4 范数与谱半径

(i)上式中ai取遍A的全体特征值.因此:

(ii)A的幂的特征值就是A的特征值的幂：

(iii)对应的：

(iv)两边各开j次方：

(v)当j趋于无穷时,上式近似于等式：