信号与系统实验四：信号与系统复频域分析（2 学时）

注明：这是学校专业课实验，利用网站做一个学习和记录。有错的地方希望好心人指点一下。

一、实验目的

1.学会用 MATLAB 进行部分分式展开；

2.学会用 MATLAB 分析 LTI 系统的特性；

3.学会用 MATLAB 进行 Laplace 正、反变换。

4.学会用 MATLAB 画离散系统零极点图；

5.学会用 MATLAB 分析离散系统的频率特性；

二、实验原理

1．用 MATLAB 进行部分分式展开

用 MATLAB 函数 residue 可以得到复杂有理分式 F(s)的部分分式展开式，其调用格式为

$\left [ r,p,k \right ]= residue(num,den)$

其中，num,den 分别为 F(s)的分子和分母多项式的系数向量，r 为部分分式的系数，p 为极点，k 为 F(s)中整式部分的系数，若 F(s)为有理真分式，则 k 为零。

例 6-1 用部分分式展开法求 F(s)的反变换 $F(s)=\frac{s+2}{s^{3}+4s^{2}+3s}$

解:其 MATLAB 程序为

format rat;num=[1,2];den=[1,4,3,0];[r,p]=residue(num,den)

程序中 format rat 是将结果数据以分数形式显示

F(s)可展开为 $F(s)=\frac{2/3}{s}+\frac{-0.5}{s+1}+\frac{-1/6}{s+3}$

所以，F(s)的反变换 $f(t)=\left [ \frac{2}{3} -\frac{1}{2}e^{-t}-\frac{1}{6}e^{-3t}\right ]u(t)$

2．用 MATLAB 分析 LTI 系统的特性

系统函数 H（s）通常是一个有理分式，其分子和分母均为多项式。计算 H（s）的零极点可以应用 MATLAB 中的 roots 函数，求出分子和分母多项式的根，然后用 plot 命令画图。

在 MATLAB 中还有一种更简便的方法画系统函数 H（s）的零极点分布图，即用 pzmap

函数画图。其调用格式为

pzmap(sys)

sys 表示 LTI 系统的模型，要借助 tf 函数获得，其调用格式为

sys=tf(b,a)

式中，b 和 a 分别为系统函数 H（s）的分子和分母多项式的系数向量。

如果已知系统函数H(s)，求系统的单位冲激响应 $H(t)$ 和频率响应 $H(j\omega )$ 可以用以前介绍过的 impulse 和 freqs 函数。

例 6-2 已知系统函数为 $H(s)=\frac{1}{s^{3}+2s^{2}+2s+1}$

试画出其零极点分布图，求系统的单位冲激响应 h(t)和频率响应 $H(j\omega )$ ，并判断系统

是否稳定。

解：其 MATLAB 程序如下：

num=[1];den=[1,2,2,1];sys=tf(num,den);figure(1);pzmap(sys);t=0:0.02:10;h=impulse(num,den,t);figure(2);plot(t,h)title('Impulse Response')[H,w]=freqs(num,den);figure(3);plot(w,abs(H))xlabel('\omega')title('Magnitude Response')

3．用 MATLAB 进行 Laplace 正、反变换

MATLAB 的符号数学工具箱提供了计算 Laplace 正、反变换的函数 Laplace 和 ilaplace, 其调用格式为上述两式右端的 f 和 F 分别为时域表示式和 s 域表示式的符号表示，可以应用函数 sym 实现，其调用格式为

S=sym(A)

式中，A 为待分析表示式的字符串，S 为符号数字或变量。

$F=laplace(f)$

$f=ilaplace(f))$

例 6-3 试分别用 Laplace 和 ilaplace 函数求

（1） $f(t)=e^{-t}sin(at)u(t)$ 的 Laplace 变换；

（2） $F(s)=\frac{s^{2}}{s^{2}+1}$ 的 Laplace 反变换。

解：

（1）其程序为

%（1）其程序为 
f=sym('exp(-t)*sin(a*t)'); 
F=laplace(f) 
%或者
syms a t 
F=laplace(exp(-t)*sin(a*t)) 
%（2）其程序为
F=sym('s^2/(s^2+1)'); 
ft=ilaplace(F) 
%或 
syms s 
ft= ilaplace(s^2/(s^2+1))

4．离散系统零极点图

离散系统可以用下述差分方程描述： $\sum_{i=0}^{N}a_{i}y(k-i)=\sum_{m=0}^{M}b_{m}f(k-m)$

Z变换后可得系统函数： $H(z)=\frac{Y(z)}{F(z)}=\frac{b_{0}+b_{1}z^{-1}+...+b_{M}z^{-M}}{a_{0}+a_{1}z^{-1}+...+a_{N}z^{-N}}$

用 MATLAB 提供的 root 函数可分别求零点和极点，调用格式是

p=[a0,a1…an],q=[b0,b1…bm,0,0…0], 补 0 使二者维数一样。画零极点图的方法有多种，可以用 MATLAB 函数[z,p,k]=tf2zp(b,a)和 zplane(q,p)，也可用 plot 命令自编一函数 ljdt.m,话图时调用。

%注意：建立函数时以lidt.m为文件名，切函数有参数不足报错不用细究
function ljdt(A,B)% The function to draw the pole-zero diagram for discrete systemp=roots(A)； %求系统极点q=roots(B)； %求系统零点p=p'； %将极点列向量转置为行向量q=q'；%将零点列向量转置为行向量x=max(abs([p q 1]))； %确定纵坐标范围x=x+0.1；y=x； %确定横坐标范围clfhold onaxis([-x x -y y]) %确定坐标轴显示范围w=0:pi/300:2*pi；t=exp(i*w)；plot(t) %画单位园axis('square')plot([-x x],[0 0])  %画横坐标轴plot([0 0],[-y y]) %画纵坐标轴text(0.1,x,'jIm[z]')text(y,1/10,'Re[z]')plot(real(p),imag(p),'x') %画极点plot(real(q),imag(q),'o') %画零点title('pole-zero diagram for discrete system') %标注标题hold offend

例 6-4 求系统函数零极点图 $H(z)=\frac{z+1}{3z^{5}-z^{4}+1}$

%在建立好上述函数的情况下，另起脚本，运行代码
a=[3 -1 0 0 0 1];b=[1 1];ljdt(a,b)p=roots(a)q=roots(b)pa=abs(p)

5．离散系统的频率特性

离散系统的频率特性可由系统函数求出，既令 $z=e^{j\omega }$ ,MATLAB 函数 freqz 可计算频率特性，调用格式是：

[H，W]=freqz(b,a,n)，

b 和 a 是系统函数分子分母系数，n是 $0-\pi$ 范围 n 个等份点，默认值 512，H 是频率响应函数值，W 是相应频率点； [H，W]=freqz(b,a,n,’whole’), n 是 $0-2\pi$ 范围 n 个等份点freqz(b,a,n)，直接画频率响应幅频和相频曲线；

例 6-5 系统函数 $H(z)\frac{z-0.5}{z}$

运行如下语句，可得 10 个频率点的计算结果

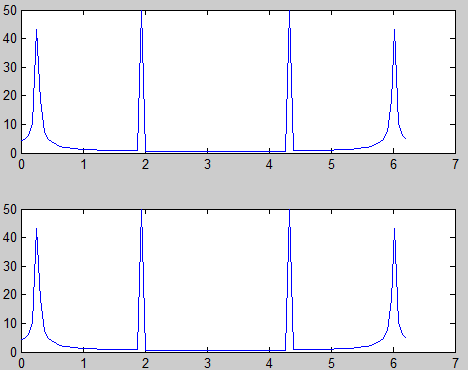
A=[1 0];B=[1 -0.5];[H,W]=freqz(B,A,10)继续运行如下语句，可将 400 个频率点的计算结果用 plot 语句画幅频和相频曲线B=[1 -0.5];A =[1 0];[H,w]=freqz(B,A,400,'whole');Hf=abs(H);Hx=angle(H);clffigure(1)plot(w,Hf)title('离散系统幅频特性曲线')figure(2)plot(w,Hx)title('离散系统相频特性曲线')%还可用 freqz 语句直接画图，注意区别A=[1 0];B=[1 -0.5];[H,W]=freqz(B,A,10)继续运行如下语句，可将 400 个频率点的计算结果用 plot 语句画幅频和相频曲线B=[1 -0.5];A =[1 0];[H,w]=freqz(B,A,400,'whole');Hf=abs(H);Hx=angle(H);clffigure(1)plot(w,Hf)title('离散系统幅频特性曲线')figure(2)plot(w,Hx)title('离散系统相频特性曲线')%还可用 freqz 语句直接画图，注意区别%A=[1 0];%B=[1 -0.5];%freqz(B,A,400)

例 6-6 用几何矢量法，自编程序画频率响应

原理：频率响应 $H(e^{j\omega })=\frac{\prod_{j-1}^{M}e^{j\omega }-q^{j}}{\prod_{i=1}^{N}e^{j\omega }-p^{i}}$

编程流程：定义 Z 平面单位圆上 k 个频率等分点；求出系统函数所有零点和极点到

这些等分点的距离；求出系统函数所有零点和极点到这些等分点的矢量的相角；求出单位圆上各频率等分点的

$\left | H(e^{j\omega}) \right |$ 和 $\varphi (\omega )$

画指定范围内的幅频与相频。若要画零极点图，可调用 ljdt.m 函数。

%与例4相同，建立一个函数以dplxy.m 命名，
function dplxy(k,r,A,B)%The function to draw the frequency response of discrete systemp=roots(A); %求极点q=roots(B); %求零点figure(1)ljdt(A,B) %画零极点图w=0:l*pi/k:r*pi;y=exp(i*w);%定义单位圆上的 k 个频率等分点N=length(p);%求极点个数M=length(q);%求零点个数yp=ones(N,1)*y;%定义行数为极点个数的单位圆向量yq=ones(M,1)*y;%定义行数为零点个数的单位圆向量vp=yp-p*ones(1,r*k+1);%定义极点到单位圆上各点的向量vq=yq-q*ones(1,r*k+1);%定义零点到单位圆上各点的向量Ai=abs(vp);%求出极点到单位圆上各点的向量的模Bj=abs(vq);%求出零点到单位圆上各点的向量的模Ci=angle(vp);%求出极点到单位圆上各点的向量的相角Dj=angle(vq);%求出零点到单位圆上各点的向量的相角fai=sum(Dj,1)-sum(Ci,1); %求系统相频响应H=prod(Bj,1)./prod(Ai,1); %求系统幅频响应figure(2)plot(w,H); %绘制幅频特性曲线title('离散系统幅频特性曲线')xlabel('角频率')ylabel('幅度')figure(3)plot(w,fai)title('离散系统的相频特性曲线')xlabel('角频率')ylabel('相位')end

已知系统函数 $H(z)=\frac{5/4(1-z^{-1})}{1-1/4z^{-1}}$ ，画频率响应和零极点图。

%同例4，在上述dplxy.m函数建好情况下，另建脚本运行
A=[1 -1/4];B=[5/4 -5/4];dplxy(500,2,A,B) %绘制系统 2π 频率范围内 500 个频率点的幅频和相频特性曲线

三。上机实验

1.验证实验原理中的相关程序。

2 ．求信号 $f(t)=te^{-3t}u(t)$ 的拉普拉斯变换

%上机实验 f=t*exp(-3*t)u(t)的拉普拉斯变化
f=str2sym('t*exp(-3*t)'); 
F=laplace(f) 
%或
syms  t 
F=laplace(t*exp(-3*t))

3 ．求函数 $F(s)=\frac{s^{3}+5s^{2}+9s+7}{s^{2}+3s+2}$ 的反变换

%求F（s）=s^3+s^2+9*s+7/(s^2+3*s+2)的反变化
%反变换:
F=str2sym('(s^3+5*s^2+9*s+7)/(s^2+3*s+2)'); 
ft=ilaplace(F)

4 ．已知连续系统的系统函数如下，试用 MATLAB 绘制系统的零极点图，并根据零极点图

判断系统的稳定性

$H(s)=\frac{s^{2}+s+2}{3s^{3}+5s^{2}+4s-6}$

% 已知连续系统的系统函数如下，试用 MATLAB 绘制系统的零极点图，并根据零极点图，判断系统的稳定性
%H(s)=s^2+s+2/(3*s^3+5*s^2+4*s-6)num=[1,1,2];%用向 量表示 分子系数
den=[3,5,4,-6];%用向量表示分母系数
sys=tf(num,den);%系统传递函数
set(gcf,'color','w');
pzmap(sys);%绘制其零极点图
p=pole(sys);
z=zero(sys);%零极点图： X为极点， O为零点
%由零极点图看出：系统不稳定，因为有极点在右半平面

5 ．系统函数是 $1+5z^{-1}+5z^{-2}+z^{-3}$ 求频率响应

第一种方法：

（总的求他的频率响应图，有问题请指正）

num=[1,5,5,1]; 
den=[1];
sys=tf(num,den); 
figure(1);pzmap(sys); 
[H,w]=freqs(num,den); 
figure(2);plot(w,abs(H)) 
xlabel('\omega') 
title('频率响应')

第二种方法：

（分别求频率响应的幅频和相频）

num=[1,5,5,1]; 
den=[1,0,0,0];
[H,w]=freqz(num,den,400,'whole'); 
Hf=abs(H);
Hx=angle(H);
clf
figure(1) 
plot(w,Hf)
title('幅频特性') 
figure(2)
plot(w,Hx)
title('相频特性')