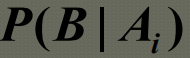概率的定义，性质

定义 设 $E$ 是随机试验，$S$ 是它的样本空间。
   对于 $E$ 的每一个事件 $A$ 赋予一个实数，记为 $P(A)$，称为事件 $A$ 的概率。
   如果集合函数 $P(\cdot )$ 满足下列条件：

   $1^{\circ }$ 非负性： 对于每一事件 $A$，有 $P(A)⩾0$；
   $2^{\circ }$ 规范性： 对于必然事件 $S$，有 $P(S)=1$；
   $3^{\circ }$ 可列可加性： 设 $A_1,A_2,\cdots$ 是两两互不相容的事件，
            即对于 $A_i{A}_j=\varnothing$，$i\ne j$，$i,j=1,2,\cdots$，有$$P(A_1\cup A_2\cup \cdots )=P(A_1)+P(A_2)+\cdots$$

由大数定理，当 $n\to \infty$ 时频率 $f_n(A)$ 在一定意义下接近于概率 $P(A)$。
基于这一事实，我们就有理由将概率 $P(A)$ 用来表征事件 $A$ 在一次试验中发生的可能性的大小。

下面是关于概率的一些重要性质：

---

性质 1  $P(\varnothing )=0$

---

性质 2 (有限可加性) 若 $A_1,A_2,\cdots ,A_n$ 是两两互不相容的事件，则有$$P(A_1\cup A_2\cup \cdots \cup A_n)=P(A_1)+P(A_2)+\cdots +P(A_n)\text{\hspace{1em}(3.2)}$$

式 (3.2) 称为概率的有限可加性。

---

性质 3 设 $A,B$ 是两个事件，若 $A\subset B$，则有$$\begin{gathered} P(B-A)=P(B)-P(A) \\ P(B)⩾P(A) \end{gathered}$$

---

性质 4 对于任一事件 $A$，$P(A)⩽1$

---

性质 5 (逆事件的概率) 对于任一事件 $A$，有$$P(\overline{A})=1-P(A)$$

---

性质 6 (加法公式) 对于任意两事件 $A,B$ 有$$P(A\cup B)=P(A)+P(B)-P(AB)$$

推广到多个事件的情况，设 $A_1,A_2,A_3$ 为三个任意事件，则有$$\begin{array}{rl}P(A_1\cup A_2\cup A_3)& =P(A_1)+P(A_2)+P(A_3)\\ & -P(A_1{A}_2)-P(A_1{A}_3)-P(A_2{A}_3)\\ & +P(A_1{A}_2{A}_3)\end{array}$$

一般，对于任意 $n$ 个事件 $A_1,A_2,\cdots ,A_n$，可以用归纳法证得$$\begin{array}{rl}P(A_1\cup A_2\cup \cdots \cup A_n)& =\sum _{i=1}^{n}P(A_i)-\sum _{1⩽i<j⩽n}P(A_i{A}_j)\\ & +\sum _{1⩽i<j<k⩽n}P(A_i{A}_j{A}_k)+\cdots +(-1{)}^{n-1}P(A_1{A}_2\cdots A_n)\end{array}$$

---

1. 等可能概型（古典概型）

对于以下试验：
$E_1$：抛一枚硬币，观察正面 $H$ 、反面 $T$ 出现的情况。
$E_2$：抛一颗骰子，观察出现的点数。

它们具有两个共同的特点：
$1^{\circ }$ 试验的样本空间只包含有限个元素；
$2^{\circ }$ 试验中每个基本事件发生的可能性相同。

具有以上 2 个特点试验是大量存在的。

对于试验 $E_1$ ，样本空间为 { H , T } \{ H,T \} {H,T}，每个基本事件发生的概率为 $1/2$
对于试验 $E_2$ ，样本空间为 { 1 , 2 , 3 , 4 , 5 , 6 } \{ 1,2,3,4,5,6 \} {1,2,3,4,5,6}，每个基本事件发生的概率为 $1/6$

这种试验称为等可能概型。
在概率论发展初期，这种试验曾是主要的研究对象，所以也叫古典概型。

---

设试验的样本空间为 S = { e 1 , e 2 , … , e n } S=\{e_1,e_2,\dots,e_n\} S={e1​,e2​,…,en​}。
由于在试验中每个基本事件发生的可能性相同，即有
P ( { e 1 } ) = P ( { e 2 } ) = ⋯ = P ( { e n } ) P(\{e_1\}) = P(\{e_2\}) = \cdots = P(\{e_n\}) P({e1​})=P({e2​})=⋯=P({en​})又由于基本事件时两两不相容的，于是 1 = P ( S ) = P ( { e 1 } ∪ { e 2 } ∪ ⋯ ∪ { e n } ) = P ( { e 1 } ) + P ( { e 2 } ) + ⋯ + P ( { e n } ) = n P ( { e i } ) , P ( { e i } ) = 1 n , i = 1 , 2 , ⋯ , n \begin{aligned} 1 &= P(S) \\ &= P( \; \{e_1\} \; \cup \; \{e_2\} \; \cup \; \cdots \; \cup \; \{e_n\}) \\ &= P(\{e_1\}) + P(\{e_2\}) + \cdots + P(\{e_n\}) \\ &= nP(\{e_i\}) , \end{aligned} \\[1em] P(\{e_i\}) = \frac{1}{n}, \quad i=1,2,\cdots,n 1​=P(S)=P({e1​}∪{e2​}∪⋯∪{en​})=P({e1​})+P({e2​})+⋯+P({en​})=nP({ei​}),​P({ei​})=n1​,i=1,2,⋯,n

若事件 $A$ 包含 $k$ 个基本事件，即 A = { e i 1 ∪ e i 2 ∪ ⋯ ∪ e i k } A=\{ e_{i_1} \; \cup \; e_{i_2} \; \cup \; \cdots \; \cup \; e_{i_k} \} A={ei1​​∪ei2​​∪⋯∪eik​​}，
这里 $i_1,i_2,\cdots ,i_k$ 是 $1,2,\cdots ,n$ 中某 $k$ 个不同的数，则有 P ( A ) = ∑ j = 1 k P ( { e i j } ) = k n = A 包 含 的 基 本 事 件 数 S 中 基 本 事 件 的 总 数 (4.1) P(A) = \sum^k_{j=1}P(\{e_{i_j}\} ) = \frac{k}{n} = \frac{A包含的基本事件数}{S中基本事件的总数}\tag{4.1} P(A)=j=1∑k​P({eij​​})=nk​=S中基本事件的总数A包含的基本事件数​(4.1)
（4.1）式就是等可能概型中，事件 $A$ 的概率的计算公式。

---

举个栗子：

问  试验 $E_2$：将一枚硬币抛 $3$ 次，观察正面 $H$、反面 $T$ 出现的情况。
   设事件 $A_1$ 为“恰有一次出现正面”，求 $P(A_1)$。

解  $E_2$ 的样本空间： S 2 = { H H H , H H T , H T H , T H H , H T T , T H T , T T H , T T T } S_2 = \{ HHH,HHT,HTH,THH,HTT,THT,TTH,TTT\} S2​={HHH,HHT,HTH,THH,HTT,THT,TTH,TTT}   $A_1$： A 1 = { H T T , T H T , T T H } A_1 = \{ HTT,THT,TTH\} A1​={HTT,THT,TTH}   $S_2$ 中包含有限个元素，且由对称性知每个基本事件发生的可能性相同，由式 (4.1) 得：$$P(A_1)=\frac{3}{8}$$
当样本空间的元素较多时，我们一般不再将 $S$ 中的元素一一列出，而只需分别求出 $S$ 中包含的元素的个数，$A$ 中包含的元素的个数（即基本事件的个数），再由（4.1）式即可求出 $A$ 的概率。

2. 条件概率

2.1 条件概率

条件概率所考虑的是事件 $A$ 已发生的条件下，事件 $B$ 发生的概率。

设 $A,B$ 是两个事件，且 $P(A)>0$，称$$P(B|A)=\frac{P(AB)}{P(A)}\text{\hspace{1em}(5.2)}$$为事件 $A$ 发生的条件下，事件 $B$ 发生的条件概率。

---

条件概率 $P(\cdot |A)$ 符合概率定义中的三个条件：

$1^{\circ }$ 非负性： 对于每一事件 $B$，有 $P(B|A)⩾0$；
$2^{\circ }$ 规范性： 对于必然事件 $S$，有 $P(S|A)=1$；
$3^{\circ }$ 可列可加性： 设 $B_1,B_2,\cdots$ 是两两互不相容的事件，则有$$P\left(\bigcup _{i=1}^{\infty }{B}_i|A\right)=\sum _{i=1}^{\infty }P\left(B_i|A\right)$$

既然条件概率符合上述 3 个条件，那它也符合前面讲的关于概率的一些性质。
例如，对于任意事件 $B_1,B_2$，有 $P(B_1\cup B_2|A)=P(B_1|A)+P(B_2|A)-P(B_1{B}_2|A)$

2.2 乘法定理

由条件概率的定义(5.2)，立即可得下述定理：

设 $P(A)>0$ ，则有 $$P(AB)=P(B|A)P(A)\text{\hspace{1em}(5.3)}$$
式 (5.3) 称为乘法公式。

---

推广到多个事件的积事件的情况，例如 $A,B,C$ 为事件，且$P(AB)>0$，则有$$P(ABC)=P(C|AB)P(B|A)P(A)$$这里注意到由假设 $P(AB)>0$ 可推得 $P(A)⩾P(AB)>0$

---

一般地，设 $A_1,A_2,\cdots ,A_n$ 为 $n$ 个事件，$n⩾2$，且 $P(A_1{A}_2\cdots A_{n-1})>0$，则有$$P(A_1{A}_2\dots A_n)=P(A_n|A_1{A}_2\cdots A_{n-1})P(A_{n-1}|A_1{A}_2\cdots A_{n-2})\cdots P(A_2|A_1)P(A_1)$$

2.3 全概率公式

设试验 $E$ 的样本空间为 $S$，$A$ 为 $E$ 的事件，$B_1,B_2,\cdots ,B_n$ 为 $S$ 的一个划分，且 $P(B_i)>0(i=1,2,\cdots ,n)$，则$$P(A)=P(A|B_1)P(B_1)+P(A|B_2)P(B_2)+\cdots +P(A|B_n)P(B_n)\text{\hspace{1em}(5.6)}$$

式 (5.6) 称为全概率公式。

---

“划分” 的定义是这样的：

 设 $S$ 为试验 $E$ 的样本空间，$B_1,B_2,\cdots ,B_n$ 为 $E$ 的一组事件，若
 $(\text{i})$ $B_i{B}_j=\varnothing$，$i\ne j$，$i,j=1,2,\cdots ,n$;
 $(\text{ii})$ $B_1\cup B_2\cup \cdots \cup B_n=S$

则称 $B_1,B_2,\cdots ,B_n$ 为样本空间 $S$ 的一个划分。

对于每次试验，$B_1,B_2,\cdots ,B_n$ 中必有且仅有一个发生。

---

在很多实际问题中，$P(A)$ 不容易直接求得，但是却容易找到 $S$ 的一个划分 $B_1,B_2,\cdots ,B_n$，且 $P(B_i)$ 和 $P(A|B_i)$ 是已知或者很容易求的，就可以用全概率公式来求 $P(A)$。要学会灵活转化问题。

2.4 贝叶斯公式

设试验 $E$ 的样本空间为 $S$，$A$ 为 $E$ 的事件，$B_1,B_2,\cdots ,B_n$ 为 $S$ 的一个划分，
且 $P(A)>0，P(B_i)>0(i=1,2,\cdots ,n)$，则$$P(B_i|A)=\frac{P(A|B_i)P(B_i)}{\sum _{j=1}^{n}P(A|B_j)P(B_j)}，i=1,2,\cdots ,n\text{\hspace{1em}(5.7)}$$式 (5.7) 称为贝叶斯(Bayes)公式。

证  由条件概率的定义及全概率公式即得： $$P(B_i|A)=\frac{P(B_{i}A)}{P(A)}=\frac{P(A|B_i)P(B_i)}{\sum _{j=1}^{n}P(A|B_j)P(B_j)}，i=1,2,\cdots ,n$$

---

对于公式 (5.6) 和 (5.7)，取 $n=2$，将 $B_1$ 记为 $B$，此时 $B_2$ 就是 $\overline{B}$，
那么全概率公式和贝叶斯公式就分别成为：$$P(A)=P(A|B)P(B)+P(A|\overline{B})P(\overline{B})\text{\hspace{1em}(5.8)}$$$$P(B|A)=\frac{P(AB)}{P(A)}=\frac{P(A|B)P(B)}{P(A|B)P(B)+P(A|\overline{B})P(\overline{B})}\text{\hspace{1em}(5.9)}$$
(5.8) 和 (5.9) 这两个公式是常用的。

2.5 先验概率 后验概率

用一道习题来说

例  对以往数据分析结果表明，当机器正常时，产品的合格率为 $98\%$。
   当机器发生故障时，产品合格率为 $55\%$。
   每台早上机器启动时，机器正常的概率为 $95\%$。

   问：已知某天早上第一件产品是合格品时，机器正常的概率？

解  设事件 $A$ 为产品合格，事件 $B$ 为机器正常。
   依题意有 $P(A|B)=0.98，P(A|\overline{B})=0.55，P(B)=0.95$。
   要求解的问题是 $P(B|A)$，按照贝叶斯公式：$$\begin{array}{rl}P(B|A)=\frac{P(AB)}{P(A)}& =\frac{P(A|B)P(B)}{P(A|B)P(B)+P(A|\overline{B})P(\overline{B})}\\ & =\frac{0.98\times 0.95}{0.98\times 0.95+0.55\times 0.05}\\ & =0.97\end{array}$$

这里概率 $0.95$ （机器正常的概率$P(B)$）是由以往的数据分析得到的，叫做先验概率。
而在得到信息（生产出的第一件产品是合格品）之后，再加以修正的概率（已知产品合格，再来求此时机器正常的概率$P(B|A)$）叫做后验概率。

---

这样写也是一样，只是把 $P(AB)$ 用乘法公式展开了：$$P(B|A)=\frac{P(A|B)P(B)}{P(A)}$$

然后可以这样理解贝叶斯公式：

根据以往的经验，得知机器正常的概率 $P(B)=95\%$，这被称为先验概率。

现在再告诉你一条 “情报”：“产品合格” 与 “机器正常” 存在联系，而且现在产品都是合格的。

得到情报后你可能会想：
$\bullet$ 既然生产的产品都是合格的，那机器大概率是正常的。
$\bullet$ 这种情况下，机器正常的概率可能比先前知道的 $95\%$ 还要大 。

显然这条情报会影响我们对 “机器正常” 这个概率的判断。具体会产生什么影响，还要看他们之间关系的程度。

所以获得 “情报” 后，结合情报再对 “机器正常” 的概率进行估计，得到就是后验概率。