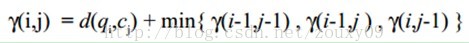算法笔记-DTW动态时间规整

动态时间规整/规划(Dynamic Time Warping, DTW)是一个比较老的算法，大概在1970年左右被提出来，最早用于处理语音方面识别分类的问题。

1.简介

简单来说，给定两个离散的序列(实际上不一定要与时间有关)，DTW能够衡量这两个序列的相似程度，或者说两个序列的距离。同时DTW能够对两个序列的延展或者压缩能够有一定的适应性，举个例子，不同人对同一个词语的发音会有细微的差别，特别在时长上，有些人的发音会比标准的发音或长或短，DTW对这种序列的延展和压缩不敏感，所以给定标准语音库，DTW能够很好得识别单个字词，这也是为什么DTW一直被认为是语音处理方面的专门算法。实际上，DTW虽然老，但简单且灵活地实现模板匹配，能解决很多离散时间序列匹配的问题，视频动作识别，生物信息比对等等诸多领域都有应用。

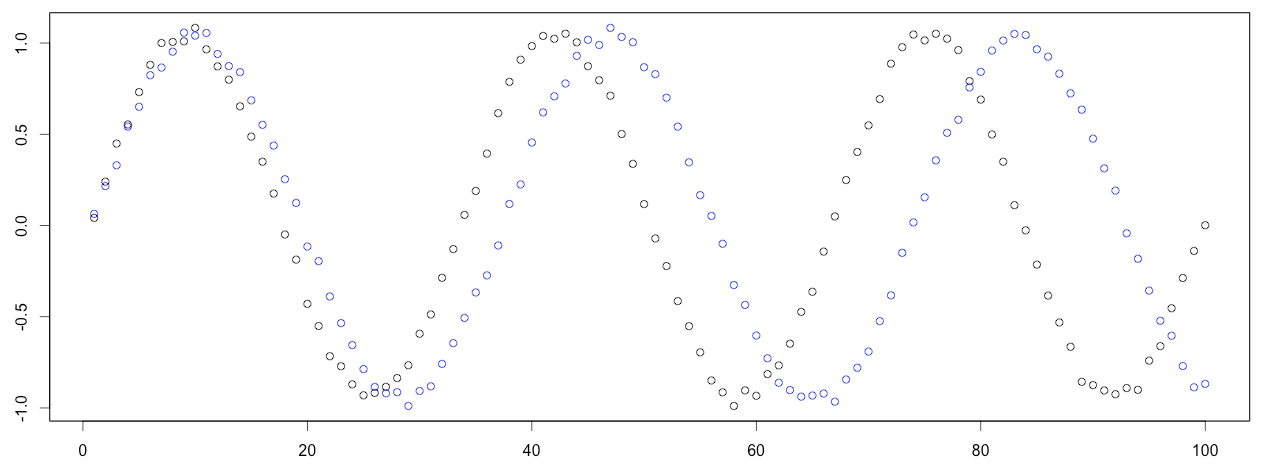
例如下图，有两个呈现正弦规律序列，其中蓝色序列是稍微被拉长了。即使这两个序列，不重合，但是我们也可以有把握说这两个序列的相似程度很高(或者说这两个序列的距离很小）。

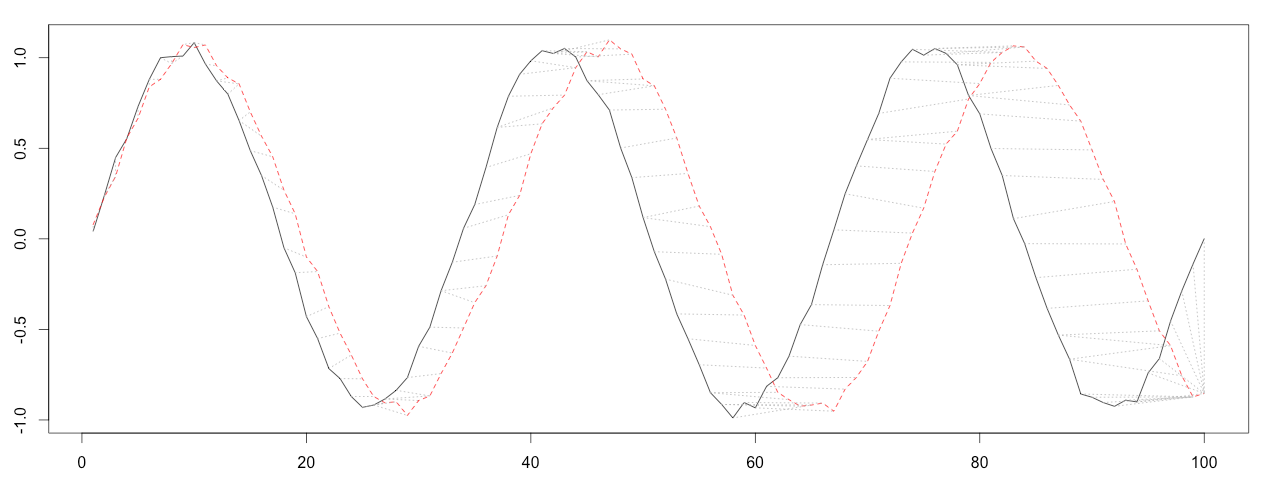
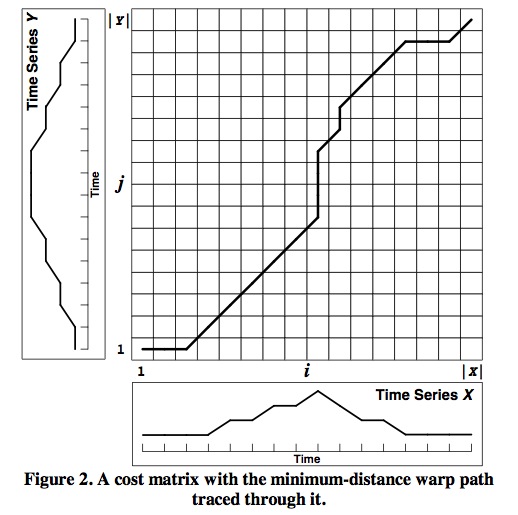
DTW能够计算这两个序列的相似程度，并且给出一个能最大程度降低两个序列距离的点到点的匹配。见下图，其中黑色与红色曲线中的虚线就是表示点点之间的一个对应关系。

也就是说，两个比对序列之间的特征是相似的，只是在时间上有不对齐的可能，这个算法名中的Time Warping，指的就是对时间序列进行的压缩或者延展以达到一个更好的匹对。

2.简单的例子

比如说，给定一个样本序列X和比对序列Y,Z：

X：3，5，6，7，7，1

Y：3，6，6，7，8，1，1
Z：2，5，7，7，7，7，2

请问是X和Y更相似还是X和Z更相似？

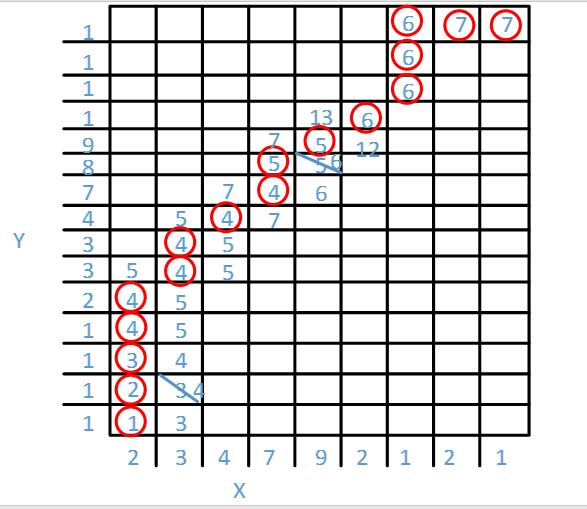
DTW首先会根据序列点之间的距离(欧氏距离)，获得一个序列距离矩阵 $M$，其中行对应X序列，列对应Y序列，矩阵元素为对应行列中X序列和Y序列点到点的欧氏距离：

X和Y的距离矩阵：

X/Y	3	6	6	7	8	1	1
3	0	3	3	4	5	2	2
5	2	1	1	2	3	4	4
6	3	0	0	1	2	5	5
7	4	1	1	0	1	6	6
7	4	1	1	0	1	6	6
1	2	5	5	6	7	0	0

然后根据距离矩阵生成1损失矩阵(Cost Matrix)或者叫累积距离矩阵 $M_c$，其计算方法如下：
1. 第一行第一列元素为 $M$ 的第一行第一列元素，在这里就是0；
2. 其他位置的元素 ($M_c(i,j)$)的值则需要逐步计算，具体值的计算方法为 $M_c(i,j)=Min(M_c(i-1,j-1),M_c(i-1,j),M_c(i,j-1))+M(i,j)$，得到的$M_c$如下：

X/Y	3	6	6	7	8	1	1
3	0	3	6	10	15	17	19
5	2	1	2	4	7	11	15
6	5	1	1	2	4	9	14
7	9	2	2	1	2	8	14
7	13	3	3	1	2	8	14
1	15	8	8	7	8	2	2

最后，两个序列的距离，由损失矩阵最后一行最后一列给出，在这里也就是2。

同样的，计算X和Z的距离矩阵：

X/Z	2	5	7	7	7	7	2
3	1	2	4	4	4	4	1
5	3	0	2	2	2	2	3
6	4	1	1	1	1	1	4
7	5	2	0	0	0	0	5
7	5	2	0	0	0	0	5
1	1	4	6	6	6	6	1

和损失矩阵：

X/Z	2	5	7	7	7	7	2
3	1	3	7	11	15	19	20
5	4	1	3	5	7	9	12
6	8	2	2	3	4	5	9
7	13	4	2	2	2	2	7
7	18	6	2	2	2	2	7
1	19	10	8	8	8	8	3

所以，X和Y的距离为2，X和Z的距离为3，X和Y更相似。

3.定义

有一个具体例子作为帮助，我们再来定义DTW算法。

假设给定两个序列，样本序列$X=(x_1,...,x_N)$和测试序列$Y=(y_1,...,y_N)$，同时给定一个序列中点到点的距离函数$d(i,j)=f(x_i,y_j)\geq 0$(一般为欧氏距离，实际上也可以是别的函数)。

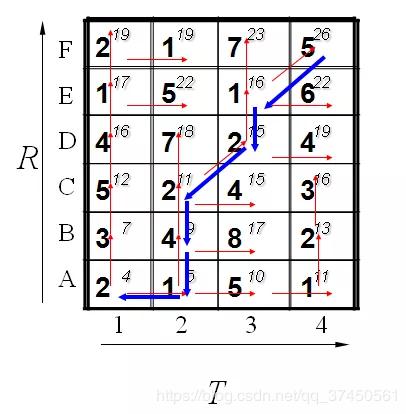
那么DTW的核心在于求解扭曲曲线(Warping Curve)或者说扭曲路径，也就是点点之间的对应关系。我们表示为$\phi(k)=(\phi_x(k),\phi_y(k))$，其中$\phi_x(k)$的可能值为1,2…N，$\phi_y(k)$的可能值为1,2…M，k=1…T。也就是说，求出T个从X序列中点到Y序列中点的对应关系，例如若$\phi(k)=(1,1)$, 那么就是说X曲线的第一个点与Y曲线的第一个点是一个对应。

给定了$\phi(k)$，我们可以求解两个序列的累积距离(Accumulated Distortion)：

$$d_\phi(X,Y) = \sum\limits_{k=1}^T d((\phi_x(k),\phi_y(k))$$

DTW的最后输出，就是要找到一个最合适的$\phi(k)$扭曲曲线，使得累积距离最小，也就是损失矩阵的最后一行最后一列的值：

$$DTW(X,Y) = \min_{\phi}d_\phi(X,Y)$$

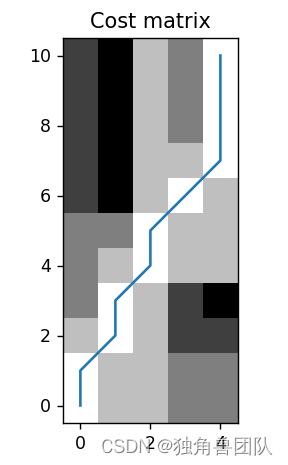
换句话说，就是给定了距离矩阵，如何找到一条从左上角到右下角的路径，使得路径经过的元素值之和最小。这个问题可以由动态规划（Dynamic Programming）解决（时间复杂度O(N+M)），也就是上面例子中，计算损失矩阵的过程，实际上不需要把整个矩阵都求解出来，大致将对角线上的元素求解出来即可。

4.讨论

实际上，虽然这个算法简单，但是有很多值得讨论的细节。

约束条件

首先，路径的寻找不是任意的，一般来说有三个约束条件：

1. 单调性：$\phi_x(k+1)\geq\phi_x(k)$且$\phi_y(k+1)\geq\phi_y(k)$，也就是说扭曲曲线不能往左或者往上后退，否则会出现无意义的循环；
2. 连续性：$\phi_x(k+1)-\phi_x(k)\leq1$, 即扭曲曲线不能跳跃，必须是连续的，保证两个序列里的所有点都被匹配到，但这个条件可以一定程度上被放松；
3. 边界条件确定性：$\phi_x(1)=\phi_y(1)=1$，$\phi_x(T)=N$，$\phi_y(T)=M$，即路径一定从左上开始，结束于右下，这个条件也可以被放松，以实现局部匹配。

除此之外，我们还可以增加别的约束：

1. 全局路径窗口(Warping Window): $|\phi_x(s)-\phi_y(s)|\leq r$ ，比较好的匹配路径往往在对角线附近，所以我们可以只考虑在对角线附近的一个区域寻找合适路径(r就是这个区域的宽度);
2. 斜率约束(Slope Constrain)： $\dfrac{\phi_x(m)-\phi_x(n)}{\phi_y(m)-\phi_y(n)}\leq p$ 和 $\dfrac{\phi_y(m)-\phi_y(n)}{\phi_x(m)-\phi_x(n)}\leq q$， 这个可以看做是局部的Warping Window，用于避免路径太过平缓或陡峭，导致短的序列匹配到太长的序列或者太长的序列匹配到太短的序列。

步模式

实际上，这些步模式(Step Pattern)一定程度上涵盖了不同的约束，步模式指的是生成损失矩阵时的具体算法，例如在例子中使用的是$M_c(i,j)=Min(M_c(i-1,j-1),M_c(i-1,j),M_c(i,j-1))+M(i,j)$准对称步模式。实际上还有很多其他步模式，不同的步模式会影响最终匹配的结果。关于不同的步模式，可以参见[2]第四章。常用的有对称，准对称和非对称三种。

标准化

序列的累积距离，可以被标准化，因为长的测试序列累积距离很容易比短的测试序列累积距离更大，但这不一定说明后者比前者与样本序列更相似，可以通过标准化累积距离再进行比较。不同的步模式会需要的不同的标准化参数。

点与点的距离函数

除了测试序列以外，DTW唯一需要的输入，就是距离函数$d$（除了欧氏距离，也可以选择Mahalanobis距离等），所以不需要考虑输入的具体形式（一维或多维，离散或连续），只要能够给定合适的距离函数，就可以DTW比对。前面说到，DTW是对时间上的压缩和延展不敏感，但是对值的大小是敏感的，可以通过合理选取距离函数来让DTW适应值大小的差异。

5.具体应用场景

这里讨论两个具体应用DTW的可能场景：

分类

气象指数在旱季和雨季的样本序列分别为$X_1$和$X_2$，现有一段新的气象指数$Y$,要判断该气象指数测得时，是雨季还旱季？

算出DTW($X_1$,$Y$)和DTW($X_2$,$Y$)，小者即为与新测得气象指数更贴近，根据此作判断。

DTW就是一个很好的差异比较的工具，给出的距离(或标准化距离)能够进一步输入到KNN等分类器里（KNN就是要找最近的邻居，DTW能够用于衡量“近”与否），进行进一步分类，比对。

点到点匹配

给定标准语句的录音$X$，现有一段新的不标准的语句录音 Y <script type="math/tex" id="MathJax-Element-37">Y</script>，其中可能缺少或者掺入了别的字词。如何确定哪些是缺少的或者哪些是掺入别的?

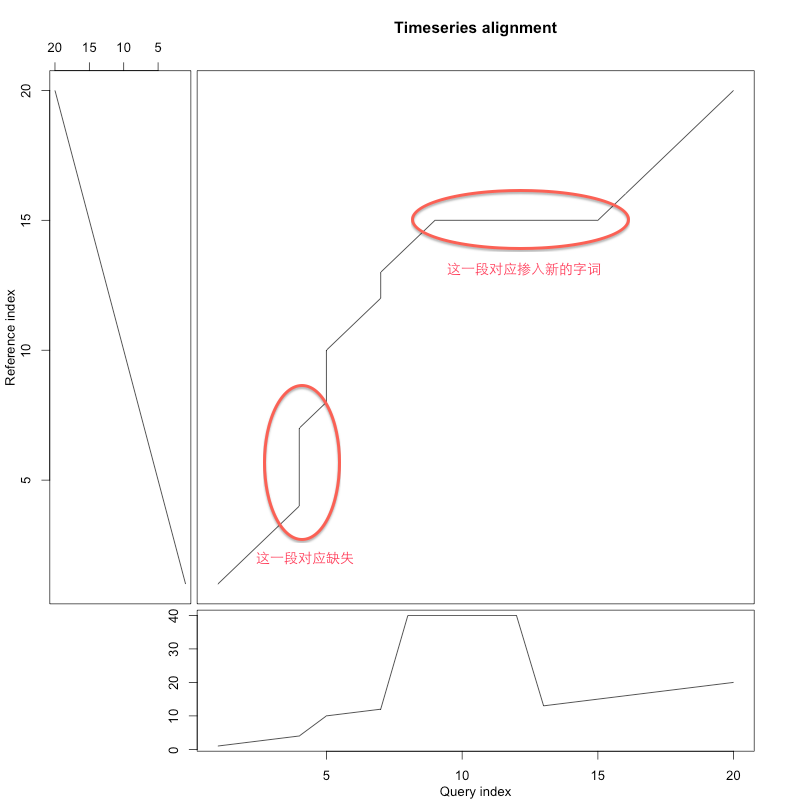
通过DTW的扭曲路径，我们可以大致得到结论：

DTW的输出是很丰富的，除了距离外，还提供了扭曲路径，可用于点到点的匹配，这个信息是非常丰富的，能够看到序列的比对，发现异常的序列。

---

References
1.Giorgino, Toni. “Computing and visualizing dynamic time warping alignments in R: the dtw package.” Journal of statistical Software 31.7 (2009): 1-24.
2.Rabiner, Lawrence R., and Biing-Hwang Juang. Fundamentals of speech recognition. Vol. 14. Englewood Cliffs: PTR Prentice Hall, 1993.