今天和大家分享一下我刚刚学习到的DTW算法。
主要从以下几个方面进行介绍:
1. DTW算法的提出和应用场景。
2. DTW算法的基本原理和计算过程。
3. DTW算法的具体代码实现。
一、DTW算法的提出和应用场景
Dynamic Time Warping(简称:DTW)算法诞生有一定的历史了(日本学者Itakura提出),它出现的目的也比较单纯,是一种衡量两个长度不同的时间序列的相似度的方法。应用也比较广,主要是在模板匹配中,比如说用在孤立词语音识别(识别两段语音是否表示同一个单词),手势识别,视频动作识别,数据挖掘和信息检索等中,曾经是语音识别的一种主流方法。
二、DTW算法的基本原理和计算过程
前言:
在时间序列中,需要比较相似性的两段时间序列的长度可能并不相等。其中,在语音识别领域表现为不同人的语速不同。因为语音信号具有相当大的随机性,即使同一个人 在不同时刻发同一个音,也不可能具有完全的时间长度。而且同一个单词内的不同音素的发音速度也不同,比如有的人会把“A”这个音拖得很长,或者把“i”发的很短。在这些复杂情况下,使用传统的欧几里得距离无法直接有效地求出两个时间序列之间的距离(或者相似性)。
反映在视频动作识别上,我们就可以将许多时间长短不一的动作视频片段和现有已知某个动作的视频片段(即模板)进行相似度的计算,以此来判断未知的动作视频片段属于哪个动作的可能性更大一些,并且在这个过程中我们还消除了两个视频片段之间的时间长短不一的问题。
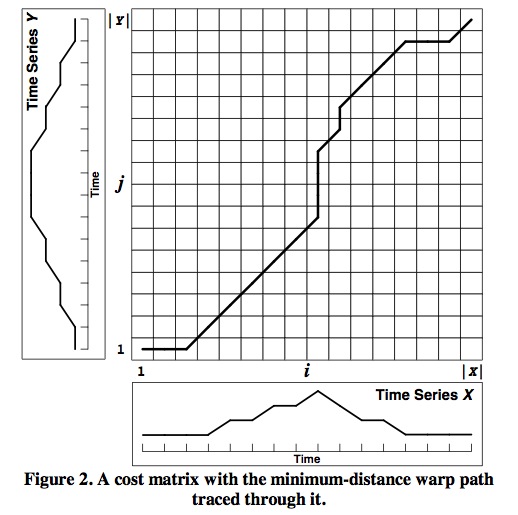
如下图表述不同序列之间的匹配:
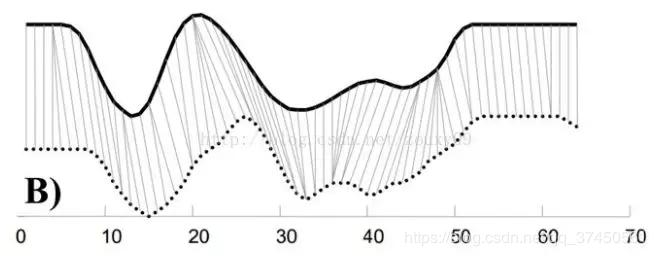
【注:实线为模板序列,虚线为测试序列。】
下面陈述一下基本的原理问题:
无论在训练和建立模型阶段还是在识别阶段,都先采用端点算法确定时间序列的起点和终点。以存入模板库(训练数据集)的各个时间序列称为参考模板(训练数据),一个参考模板可表示为R={R(1),R(2),……,R(m),……,R(M)},m为模板时间序列中的时序标号,m=1为起点序列,m=M为终点序列,因此M为该模板所包含的时间序列中序列总数,R(m)为模板时间序列中第m个序列的特征向量。所要识别的某个时间序列称为测试模板(测试数据),可表示为T={T(1),T(2),……,T(n),……,T(N)},n为测试时间序列中的时序标号,n=1为起点序列,n=N为终点序列,因此N为该测试时间序列所包含的时间序列中序列总数,T(n)为测试时间序列中第m个序列的特征向量。
假设测试模板和参考模板分别用T和R表示,为了比较它们之间的相似度,可以计算它们之间的距离 D[T,R],距离越小则相似度越高。为了计算这一失真距离,应从T和R中各个对应序列之间的距离算起。则d[T(n),R(m)]表示这两个序列的特征向量之间的距离。距离函数取决于实际采用的距离度量,在DTW算法中通常采用欧氏距离。
若N=M则可以直接计算,否则要考虑将T(n)和R(m)对齐。对齐可以采用线性扩张的方法,如果N<M可以将T线性映射为一个M个数量的序列,再计算它与{R(1),R(2),……,R(m),……,R(M)}之间的距离。但是这样的计算没有考虑到时间序列中各个段在不同情况下的持续时间会产生或长或短的变化(即:相同时间内表示同一个内容的时间长短不一。例如:人跑步,在相同的10s内,A跑100m用了3s,但是B跑100m用了10s。B比A在时间上多了7s的长度,但是是他们都是跑了100m的长度呀!),因此识别效果不可能最佳。因此更多的是采用动态规划(DP)的方法。
若把测试模板的各个***n=1N在一个二维直角坐标系中的横轴上标出,把参考模板的各***m=1M在纵轴上标出,通过这些表示***的整数坐标画出一些纵横线即可形成一个网络(矩阵),网络中的每一个交叉点(n,m)表示测试模式和参考模式中某一序列的交汇点。DP算法可以归结为寻找一条通过此网络中若干格点的路径,路径通过的格点即为测试模板和参考模板中进行计算某两个序列相似度的序列标号,每个格点存放的就是两个序列相似度。当然路径不是随意选择的,首先任何一种时间序列的序列产生的快慢都有可能变化,但是其各部分的先后发生的顺序不可能改变,因此所选的路径必定是从左下角出发,在右上角结束。
路径通过的所有格点的序列标号依次为{(1 ,1 ),(1 ,2 ),……,(i ,j ),……,(N ,M )}。如果路径已经通过了格点(n ,m ),那么下一个通过的格点只可能是下列三种情况之一:
(n +1,m)
(n +1,m +1)
(n ,m+1 )
【注:以上三种情况分别表示测试模板中的当前序列比训练模板中当前序列快,一样快,慢。】谨记!!!
满足上面条件的路径可以有指数个,然后我们感兴趣的是使得下面的规整代价最小的路径,即:搜索从(1, 1)点出发到达(N, M)点时的总的积累距离,具有最小累积距离的即为最佳路径。易于证明,限定范围的任一格点(n, m)只可能有一条搜索路径通过。对于(n, m),其可达到该格点的前一个格点只可能是(n-1, m)、(n-1, m -1)和(n, m-1),那么(n, m)一定选择这3个距离之路径延伸而通过(n, m),这时此路径的积累距离为:
D[(n, m)]=d[T(n),R(m)]+min{D(n-1,m),D(n-1,m-1),D(n,m-1)}
则从(1, 1)点出发到达(N, M)点时的总的积累距离,只保留一条最佳路径。如果有必要的话,通过逐点向前寻找就可以求得整条路径。这套DP算法便是DTW算法。
举一个例子吧:
这个例子中假设标准模板R为字母ABCDEF(6个),测试模板T为1234(4个)。R和T中各元素之间的距离已经给出(可以进行序列之间的欧式距离的计算)。
【注:其中的R,T就是相当于两段动作的视频片段,而ABCDEF和1234就如组成这两段视频的图片,分别是6张和4张。现在就是比较这两段视频表示的动作之间的相似度问题。】
如下:
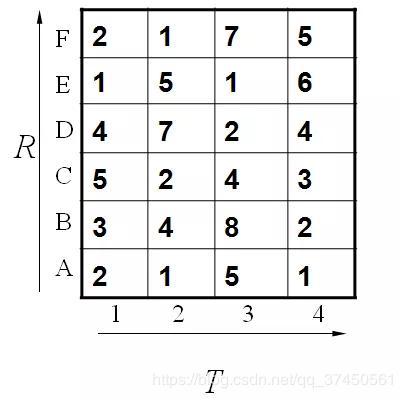
既然是模板匹配,所以各分量的先后匹配顺序已经确定了,虽然不是一一对应的。现在题目的目的是要计算出测试模板T和标准模板R之间的距离。因为2个模板的 长度不同,所以其对应匹配的关系有很多种,我们需要找出其中距离最短的那条匹配路径。现假设题目满足如下的约束:当从一个方格((i-1,j-1)或者 (i-1,j)或者(i,j-1))中到下一个方格(i,j),如果是横着或者竖着的话其距离为d(i,j),如果是斜着对角线过来的则是 2d(i,j)。其约束条件如下图像所示:
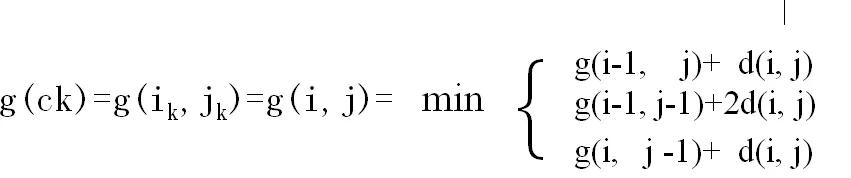
其中g(i,j)表示2个模板都从起始分量逐次匹配,已经到了M中的i分量和T中的j分量,并且匹配到此步是2个模板之间的距离。并且都是在前一次匹配的结果上加d(i,j)或者2d(i,j),然后取最小值。
所以我们将所有的匹配步骤标注后如下:
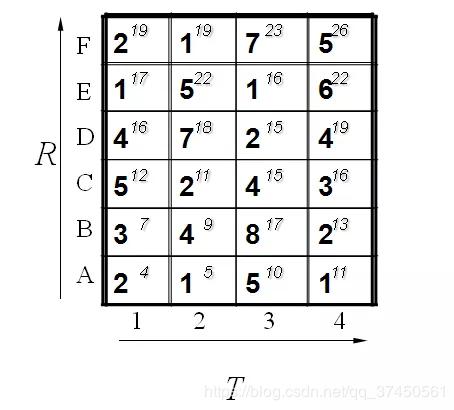
**怎么得来的呢?**比如说g(1,1)=4, 当然前提都假设是g(0,0)=0,就是说g(1,1)=g(0,0)+2d(1,1)=0+22=4。g(2,2)=9是一样的道理。首先如果从g(1,2)来算的话是g(2,2)=g(1,2)+d(2,2)=5+4=9,因为是竖着上去的。如果从g(2,1)来算的话是g(2,2)=g(2,1)+d(2,2)=7+4=11,因为是横着往右走的。如果从g(1,1)来算的话,g(2,2)=g(1,1)+2d(2,2)=4+24=12.因为是斜着过去的。
综上所述,取最小值为9. 所有g(2,2)=9.
当然在这之前要计算出g(1,1),g(2,1),g(1,2).因此计算g(I,j)也是有一定顺序的。
其基本顺序可以体现在如下:
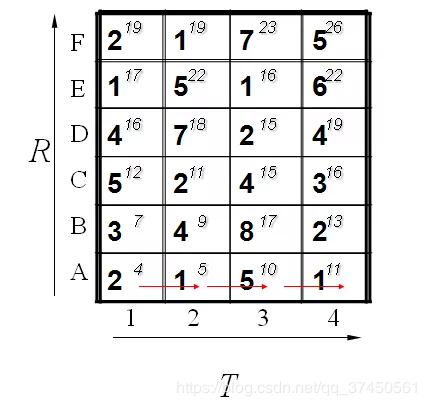
计算了第一排,其中每一个红色的箭头表示最小值来源的那个方向。当计算了第二排后的结果如下:
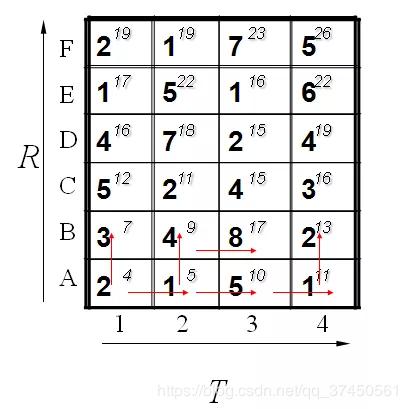
最后都算完了的结果如下:
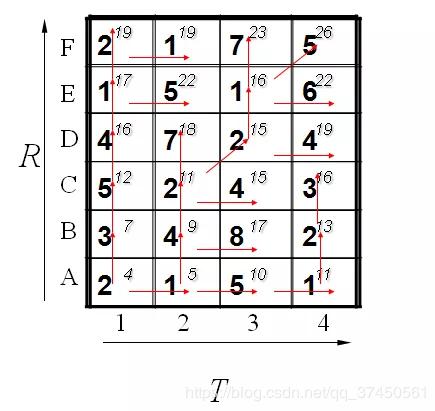
到此为止,我们已经得到了答案,即2个模板直接的距离为26. 我们还可以通过回溯找到最短距离的路径,通过箭头方向反推回去。如下所示:
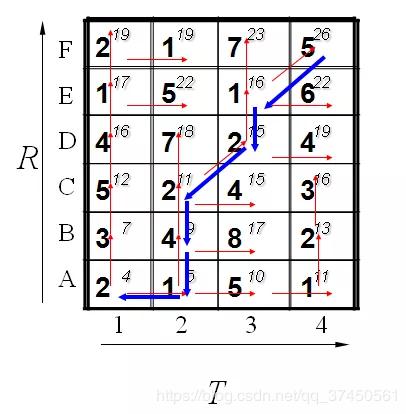
三、DTW算法的具体代码实现
1.MATLAB实现
2.Python实现
3.C++实现