目录
- 动态时间规整算法: 从DTW到FastDTW
- 总结:
- 简介[^1]
- DTW[^1]
- FastDTW:使用多级粗化的方法[^1]
- 结果
动态时间规整算法: 从DTW到FastDTW
总结:
FastDTW作者对DTW的改进点很巧妙!先通过举例说明在一些情况下目前现有的方法对DTW改进的缺陷,然后阐述自己的算法如何避免这些缺陷,最后还在三个数据集上证明在较长时间序列数据中取得线性复杂度。 说明在做算法时,在无法找到更低复杂度的方法的时候,可以考虑在牺牲一些可接受的准确度的情况下实现更低的复杂度算法!!!同时,必须通过实验证明准确度降低的程度,文中就使用正常复杂度算法和近似复杂度算法进行对比,从而计算出降低的准确率!!最后,可以吸取现有的一些改进的基础上,再进一步改进,就比在原始的DWT算法上改进的效果更好!!!!简介1
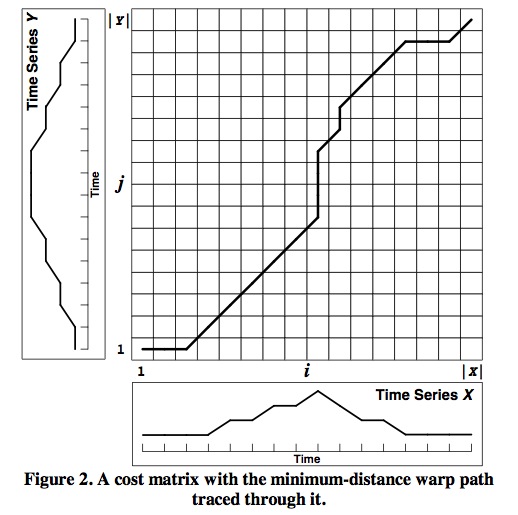
Dynamic time warping:动态时间扭曲 (DTW) 是一种在两个时间序列之间找到最佳对齐的技术,其中一个时间序列可以通过拉伸或收缩其时间轴来非线性地“扭曲”。 这种比对可用于找到对应的区域或确定两个时间序列之间的相似性。 DTW 经常用于语音识别,以确定两个波形是否代表相同的口语短语。 在语音波形中,每个语音的持续时间和声音之间的间隔是允许变化的,但整体语音波形必须相似。 DTW 还用于许多其他学科 ,包括数据挖掘、手势识别、机器人技术、制造和医学。 一个时间序列“扭曲”到一个示例如图 所示:
1) 粗化——将时间序列缩小为更小的时间序列,以更少的数据点尽可能准确地表示相同的曲线。
2) 投影——在较低分辨率下找到最小距离扭曲路径,并将其用作更高分辨率最小距离扭曲路径的初始猜测。
3) 细化——通过局部调整扭曲路径来优化从较低分辨率投影的扭曲路径。
DTW1
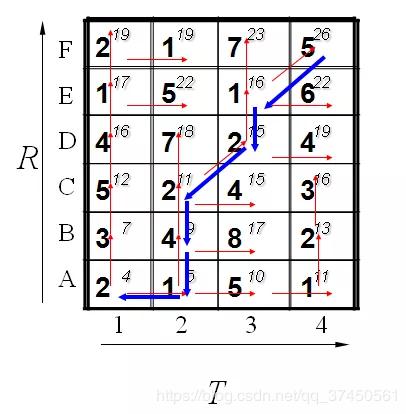
动态时间扭曲 (DTW) 是一种在两个时间序列之间找到最佳对齐的技术,其中一个时间序列可以通过拉伸或收缩其时间轴来非线性地“扭曲”。最初的实现是使用动态规划,使用数学表达如下: D ( i , j ) = D i s t ( i , j ) + m i n [ D ( i − 1 , j ) , D ( i , j − 1 ) , D ( i − 1 , j − 1 ) ] , 其中: i = 1 , 2 , ⋯ , x _ l e n + 1 ; j = 1 , 2 , ⋯ , y _ l e n + 1 D(i,j)=Dist(i,j)+min[D(i-1,j),D(i,j-1),D(i-1,j-1)], \\其中:i=1,2,\cdots,x\_len+1;j=1,2,\cdots,y\_len+1 D(i,j)=Dist(i,j)+min[D(i−1,j),D(i,j−1),D(i−1,j−1)],其中:i=1,2,⋯,x_len+1;j=1,2,⋯,y_len+1
代码实现如下2:
#参考:https://github.com/slaypni/fastdtw
import numbers
import numpy as np
from collections import defaultdict
from scipy.spatial.distance import euclideandef dtw(x, y, window=None, dist):"""@param x 序列1,可以是向量,矩阵,不局限于一个数列,但是dist要匹配@param y 序列2,可以是向量,矩阵,不局限于一个数列,但是dist要匹配@param window 序列设置要走的范围,当使用Sakoe-Chiba Bands就需要自定义缩小的范围,这里默认None会矩阵全走一遍@param dist 自定义距离计算方法,可以是欧氏距离,汉明距离等等"""len_x, len_y = len(x), len(y)if window is None:window = [(i, j) for i in range(len_x) for j in range(len_y)]# 相当于矩阵的索引 i=1,2,...len_x+1 j=1,2,...len_y+1 window = ((i + 1, j + 1) for i, j in window)# 初始化矩阵中的其他元素inf和D[0, 0]=0;D使用元组记录矩阵的值和path的i,jD = defaultdict(lambda: (float('inf'),))D[0, 0] = (0, 0, 0)# 按照公式进行规划计算for i, j in window:dt = dist(x[i-1], y[j-1])D[i, j] = min((D[i-1, j][0]+dt, i-1, j), (D[i, j-1][0]+dt, i, j-1),(D[i-1, j-1][0]+dt, i-1, j-1), key=lambda a: a[0])# 求解路径path = []i, j = len_x, len_ywhile not (i == j == 0):path.append((i-1, j-1))i, j = D[i, j][1], D[i, j][2]path.reverse()return (D[len_x, len_y][0], path)if __name__ == '__main__':x = np.array([1, 2, 3, 4, 5], dtype='float')y = np.array([2, 3, 4], dtype='float')distance, path = dtw(x, y, dist=euclidean)
FastDTW之前,后来主要有两种近似计算DWT的算法,损失一定准确率的前提下减少时间和空间复杂度:
1、约束 – 限制在成本矩阵中评估的单元数
典型有两种:constraints: Sakoe-Chiba Band (left) and Itakura Parallelogram (right);很明显,缺点是当全局最优解不在band内时,就有误差。图中的阴影区域是成本矩阵的单元格,它们被填充由每个约束的 DTW 算法。每个阴影区域或窗口的宽度由参数指定。当使用约束时,DTW 会通过约束窗口找到最优的扭曲路径。但是,如果全局最优扭曲路径不完全在窗口内,则将无法找到它。使用约束以一个常数因子加速 DTW,但如果窗口大小是时间序列长度的函数,则 DTW 仍然是 O ( N 2 ) O(N^2) O(N2)。约束在时间序列的时间对齐只有很小差异的领域中效果很好,并且最佳扭曲路径预计接近线性扭曲并以相对直线对角线穿过成本矩阵。但是,如果时间序列是在完全不同的时间开始和停止的事件,则约束效果不佳。在这种情况下,warp 路径可能会偏离线性 warp 很远,并且必须评估几乎整个成本矩阵以找到最佳 warp 路径。

下图描述了约束 DTW 不能很好地工作的情况的简化示例,必须评估整个成本矩阵以获得良好的结果。这可能发生在时间序列是受监控设备的应用程序中,这些设备以可预测的顺序发出命令(例如开/关),但命令之间的时间量(稳态条件)未指定。此类数据的示例包括航天飞机阀门特征。

2、抽象——对数据的简化表示执行 DTW
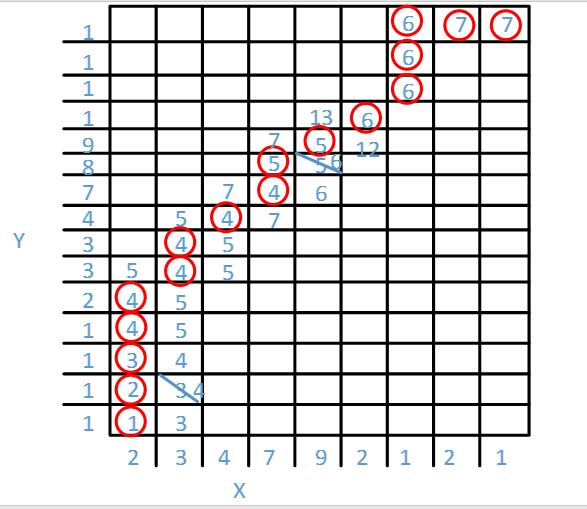
这种方法作者在FastDTW中也用上,如图所示,就是在低分辨率的矩阵中求解,也会有误差,因为路径不够细化。抽象通过对数据的简化表示进行操作来加速 DTW 算法。这些算法包括 IDDTW 、PDTW 和 COW 。时间序列的大小被缩小以使成本矩阵更易于计算。为较低分辨率的时间序列找到了一个扭曲路径并被映射回到全分辨率。
由此产生的加速取决于使用了多少抽象。显然,计算出的翘曲路径随着抽象级别的增加,它变得越来越不准确。投影低分辨率扭曲全分辨率的路径通常会创建一个远非最佳的扭曲路径。这是因为即使如果最优扭曲路径通过低分辨率单元,则将扭曲路径投影到更高的分辨率忽略了扭曲路径中可能非常重要的局部变化。因此不适用于局部变化剧烈的序列。

FastDTW:使用多级粗化的方法1
FastDTW使用下面三种方法进行改进:
1) 粗化——将时间序列缩小为更小的时间序列,以更少的数据点尽可能准确地表示相同的曲线。
2. 投影——在较低分辨率下找到最小距离扭曲路径,并将其用作更高分辨率最小距离扭曲路径的初始猜测。
3. 细化——通过局部调整扭曲路径来优化从较低分辨率投影的扭曲路径。
总结:
1、FastDTW中的分级使用更高分辨率计算,弥补了之前的Abstract的方法,原来只使用一次降低分辨率;
2、FastDTW中的细化使用半径参数控制,弥补原来的Band的方法那种不灵活性,因为Band的方法需要依靠先验知识判断最优路径大概在那些位置;而半径参数只是作为分级粗化投影的一个补充。确实很巧妙!!!

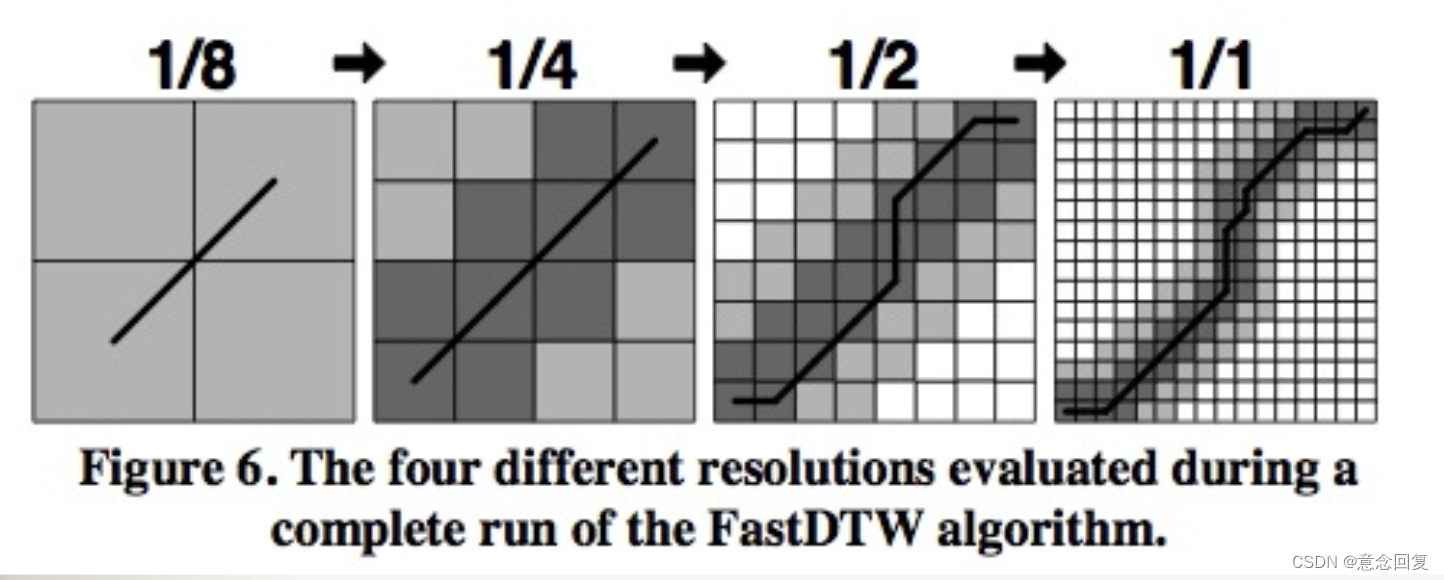
如图所示具体如下:粗化通过平均相邻的点对来减少时间序列的长度(或分辨率)。生成的时间序列比原始时间序列小两倍。粗化运行多次以产生时间序列的不同分辨率。投影采用以较低分辨率计算的扭曲路径,并以较高的分辨率确定它通过的单元格。由于分辨率增加了两倍,因此低分辨率扭曲路径中的单个点将映射到更高分辨率的至少四个点(如果 |X| = |Y |,则可能 > 4)。然后在细化过程中将此投影路径用作启发式方法,以找到更高分辨率的扭曲路径。细化在投影路径的邻域中找到最佳的扭曲路径,其中邻域的大小由半径参数控制。在我们的多级方法中,成本矩阵仅填充在从先前分辨率投影的路径的附近。由于扭曲路径的长度随着时间序列的长度线性增长,我们的多级方法是 O(N) 算法。 FastDTW 算法首先使用粗化来创建将被评估的所有分辨率。图中显示了一个时间序列上的例子在运行 FastDTW 算法时创建的四个分辨率(使用多少个分辨率的粗化矩阵按照实际序列长度确定)。
在图 中,从 1/8 分辨率的扭曲路径的投影显示为 1/4 分辨率的重度阴影单元。为了细化投影路径,使用非常具体的约束运行受约束的 DTW 算法,即仅评估投影扭曲路径中的单元格。这将通过从较低分辨率投影的扭曲路径区域找到最佳扭曲路径。然而,全局最优扭曲路径可能不完全包含在投影路径中。为了增加找到全局最优解的可能性,有一个半径参数来控制投影路径每一侧上的额外单元数,这些单元格也将在优化扭曲路径时进行评估。在图 中,半径参数设置为 1。由于半径而在扭曲路径细化过程中包含的单元格被轻微着色。一旦以 1/4 分辨率细化扭曲路径,该扭曲路径将投影到 1/2 分辨率,扩大半径 1,然后再次细化。最后,将扭曲路径投影到图 中的全分辨率 (1/1) 矩阵。投影被半径扩展并最后一次细化。这个细化的扭曲路径是算法的输出。 FastDTW 在所有分辨率下评估了 4 + 16 + 44 + 100 = 164 个单元,而 DTW 评估了 256 (162) 个单元。对于这个小问题,效率的提高并不是很显着,尤其是考虑到创建所有四个分辨率的开销,在长序列有很大差距。然而,FastDTW 评估的单元数与时间序列的长度成线性关系,而经典的动态时间扭曲算法总是评估 N 2 N^2 N2个单元(如果两个时间序列的长度均为 N)。
代码实现:

FastDTW的递归实现2:
#参考:https://github.com/slaypni/fastdtw
from __future__ import absolute_import, division
import numbers
import numpy as np
from collections import defaultdict
from scipy.spatial.distance import euclideandef dtw(x, y, window=None, dist):"""@param x 序列1,可以是向量,矩阵,不局限于一个数列,但是dist要匹配@param y 序列2,可以是向量,矩阵,不局限于一个数列,但是dist要匹配@param window 序列设置要走的范围,当使用Sakoe-Chiba Bands就需要自定义缩小的范围,这里默认None会矩阵全走一遍@param dist 自定义距离计算方法,可以是欧氏距离,汉明距离等等"""len_x, len_y = len(x), len(y)if window is None:window = [(i, j) for i in range(len_x) for j in range(len_y)]# 相当于矩阵的索引 i=1,2,...len_x+1 j=1,2,...len_y+1 window = ((i + 1, j + 1) for i, j in window)# 初始化矩阵中的其他元素inf和D[0, 0]=0;D使用元组记录矩阵的值和path的i,jD = defaultdict(lambda: (float('inf'),))D[0, 0] = (0, 0, 0)# 按照公式进行规划计算for i, j in window:dt = dist(x[i-1], y[j-1])D[i, j] = min((D[i-1, j][0]+dt, i-1, j), (D[i, j-1][0]+dt, i, j-1),(D[i-1, j-1][0]+dt, i-1, j-1), key=lambda a: a[0])# 求解路径path = []i, j = len_x, len_ywhile not (i == j == 0):path.append((i-1, j-1))i, j = D[i, j][1], D[i, j][2]path.reverse()return (D[len_x, len_y][0], path)def reduce_by_half(x):"""分辨率减半,使用平均的方法"""return [(x[i] + x[1+i]) / 2 for i in range(0, len(x) - len(x) % 2, 2)]def expand_window(path, len_x, len_y, radius):"""计算radius下的时间窗"""path_ = set(path)for i, j in path:for a, b in ((i + a, j + b)for a in range(-radius, radius+1)for b in range(-radius, radius+1)):path_.add((a, b))window_ = set()for i, j in path_:for a, b in ((i * 2, j * 2), (i * 2, j * 2 + 1),(i * 2 + 1, j * 2), (i * 2 + 1, j * 2 + 1)):window_.add((a, b))window = []start_j = 0for i in range(0, len_x):new_start_j = Nonefor j in range(start_j, len_y):if (i, j) in window_:window.append((i, j))if new_start_j is None:new_start_j = jelif new_start_j is not None:breakstart_j = new_start_jreturn windowdef fastdtw(x, y, radius, dist):min_time_size = radius + 2# 长度小于min_time_size,直接使用DTW计算if len(x) < min_time_size or len(y) < min_time_size:return dtw(x, y, dist=dist)# 每次粗化一半,得到新的序列x_shrinked = reduce_by_half(x)y_shrinked = reduce_by_half(y)# 递归计算,直到满足len(x) < min_time_size or len(y) < min_time_size则回溯distance, path = fastdtw(x_shrinked, y_shrinked, radius=radius, dist=dist)# 根据radius计算新的计算范围window = expand_window(path, len(x), len(y), radius)return dtw(x, y, window, dist=dist)结果
错误率计算:

在准确度上:
相比Band和Abstraction的方法,错误率更低,而且随着radius的增加,错误率降低,后面已经很接近DTW算法;

在时间上:
虽然在数列长度200以内体现不出区别,但是随着时间序列长度的增加,越来越接近线性时间复杂度。

参考:
Salvador S, Chan P. Toward accurate dynamic time warping in linear time and space[J]. Intelligent Data Analysis, 2007, 11(5): 561-580. ↩︎ ↩︎ ↩︎
GitHub - slaypni/fastdtw: A Python implementation of FastDTW ↩︎ ↩︎