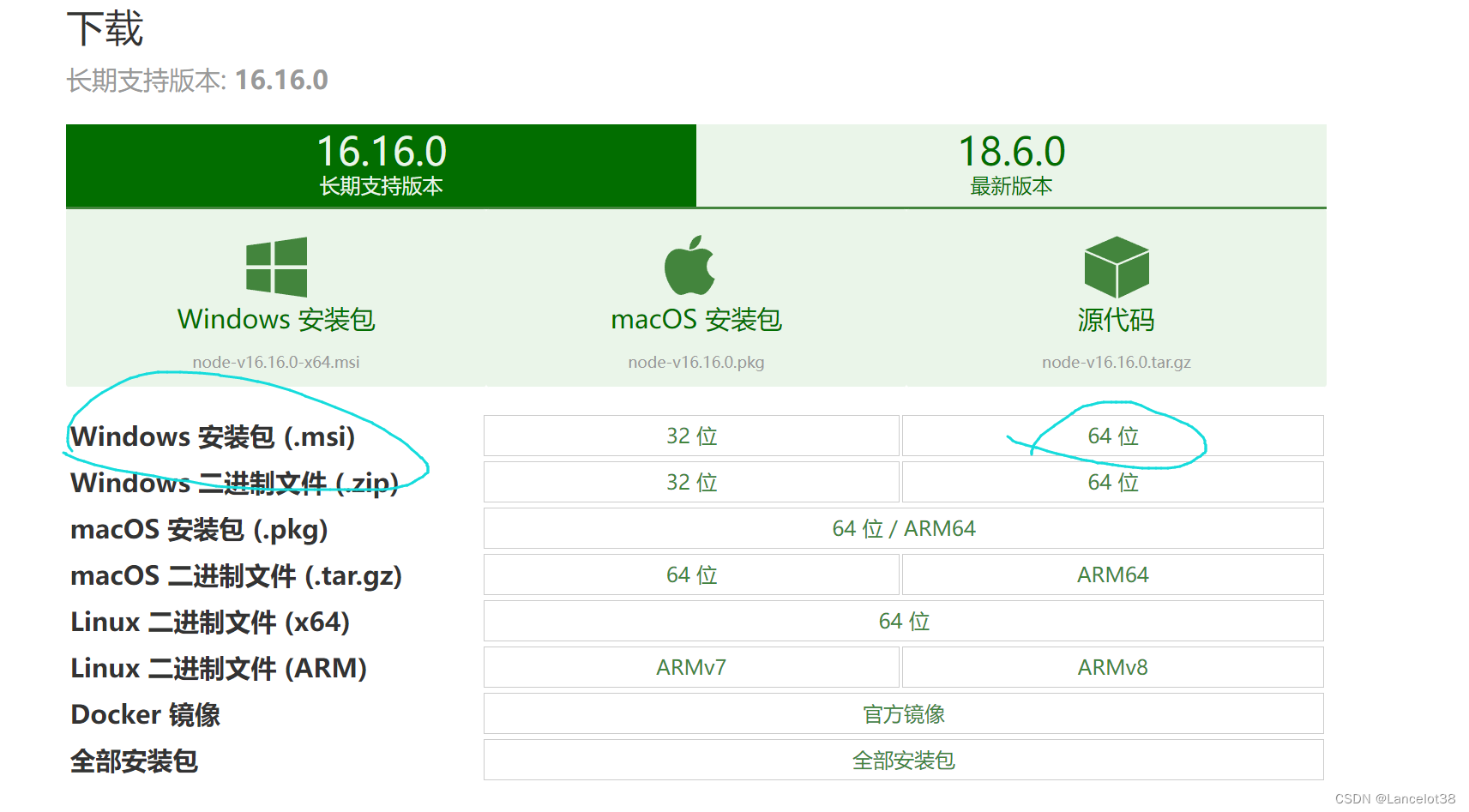
1. 进入官网选择下载版本
http://nodejs.cn/download/
2.安装过程
步骤1:选择next选项

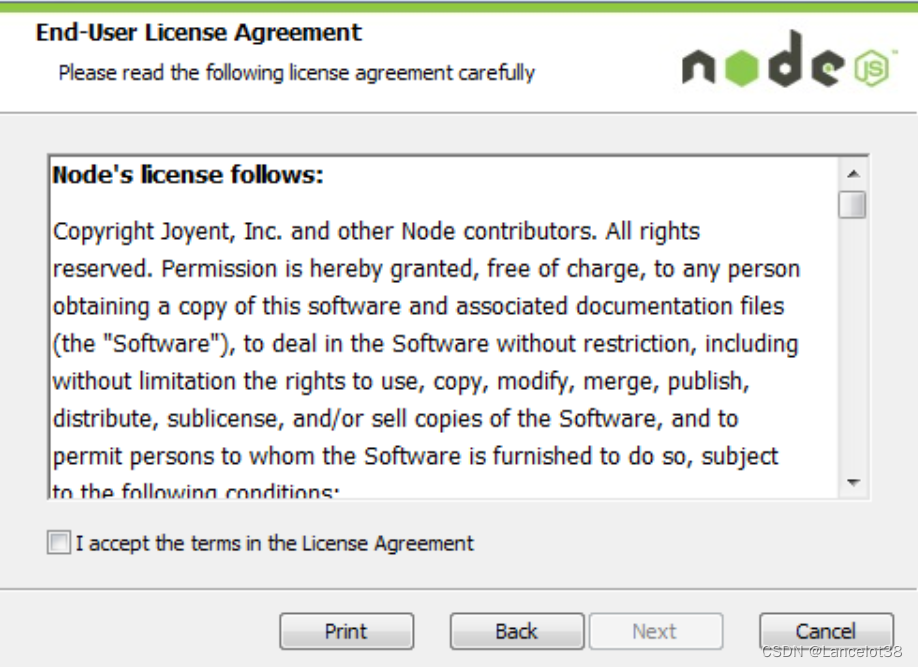
步骤2:勾选接受协议选项,点击 next(下一步)按钮 :
步骤3:其默认安装目录是C:\Program Files\nodejs\,当然你可以根据自己的需求来进行选择安装目录,一般这种配置文件我比较喜欢安装在默认位置,方便环境配置。
步骤4:这里是选择你想要安装的模式,一般无特殊需求就选择第一个就好了
步骤5: 点击 Install(安装) 开始安装Node.js。
安装过程:
点击finish完成安装,退出安装向导
3.检查是否安装成功
安装好后在本机终端中测试是否成功如果出现版本号就说明成功了
node -v npm -v

(安装成功但是有报错)
修改npm文件以解决
打开nodejs安装位置的文件夹。并打开两个文件 npm.cmd 和 npm
这是我的目录
C:\Program Files\nodejs
找到那2个文件里面的prefix -g替换为prefix --location=global
1.设置文件访问权限,分别右键点击两个文件夹,选择属性,并点击编辑。将权限改为完全控制。记住是两个文件夹都需要。
2. 将第二个文件后缀名改为.txt,然后分别以记事本的形势打开
3. 将prefix -g 替换为(注意:两个文件都需要)
prefix --location=global

4.检查是否成功,此时打开一个新的cmd命令行窗口,win+R,输入cmd,回车,此时输入
npm -v
就可以成功看见自己的版本号啦
4.配置环境变量
找到自己的nodejs安装路径,并复制。
右键点击我的电脑,点击属性->高级系统设置,点击环境变量
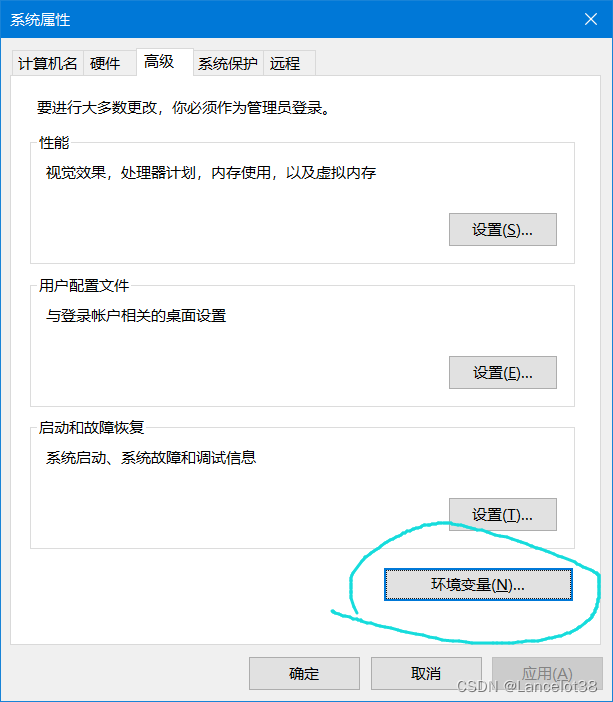
在系统环境变量 path 里添加 nodejs 的路径
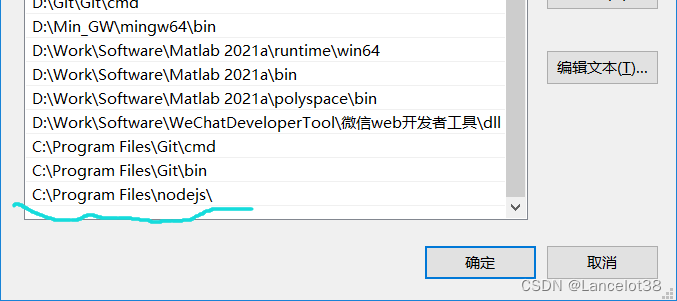
5.配置全局安装包路径
打开cmd命令行窗口,输入下面的命令,路径可以随便指定,路径不存在会自动生成
npm config set prefix “C:\Program Files\nodejs\node_global”
npm config set cache “C:\Program Files\nodejs\node_cache”

这两条命令需要分别执行,可能因为管理员权限无法生成文件夹,那么就需要手动创建,

手动创建之后,发现有报错,如图
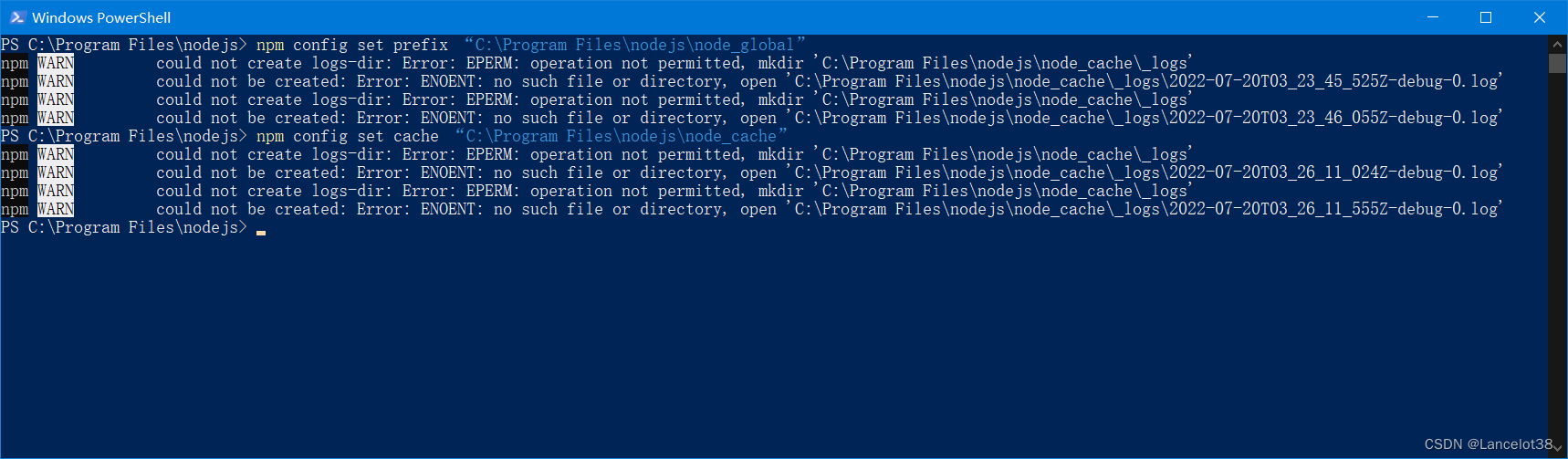
于是发现是因为文件权限不够,右键点击node,属性 => 安全 => 设置users用户完全控制权限
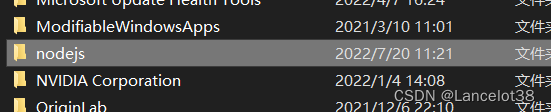
随即可以成功配置
打开环境变量设置窗口,在用户(或者系统)变量这一栏中,点击“新建”按钮,添加一个变量名“NODE_PATH",值为:
C:\Program Files\nodejs\node_modules

在“系统变量”里,找到Path这个变量,选中并编辑它。给他添加一个值:
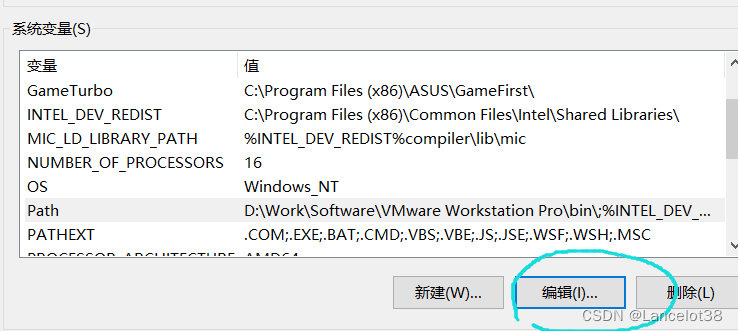
我的路径:

在“用户变量”这一栏,设置Path的变量。如果没有,就新建之,设置值为

到此nodejs设置就完成了,分别输入node -v和npm -v,得到如下图所示的结果表明nodejs环境配置成功。
以下是关于最后输入npm -v 出现 'npm’不是内部或外部命令,也不是可运行的程序问题的解决方案
首先进入环境变量中的path中找到nmp的文件位置,
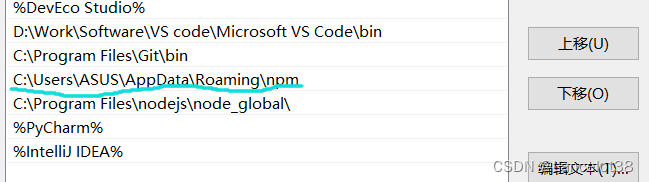
打开文件夹发现,发现没有文件或者只有一个“etc”的文件。
发现此问题之后,我们应该在环境变量中添加我们安装的npm命令行执行文件路径。
我的是在“C:\Users\ASUS\nodejs”文件下。
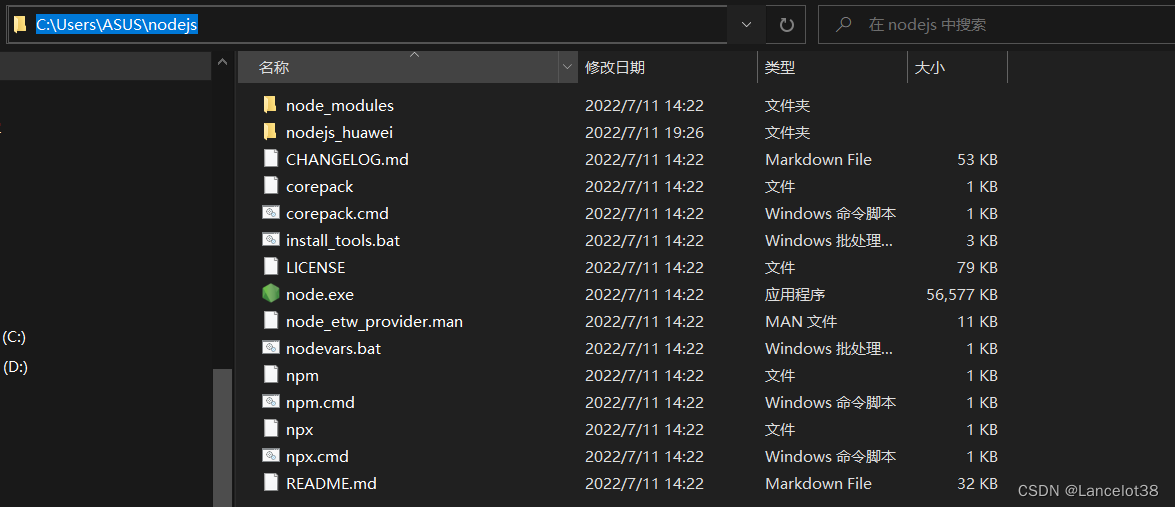
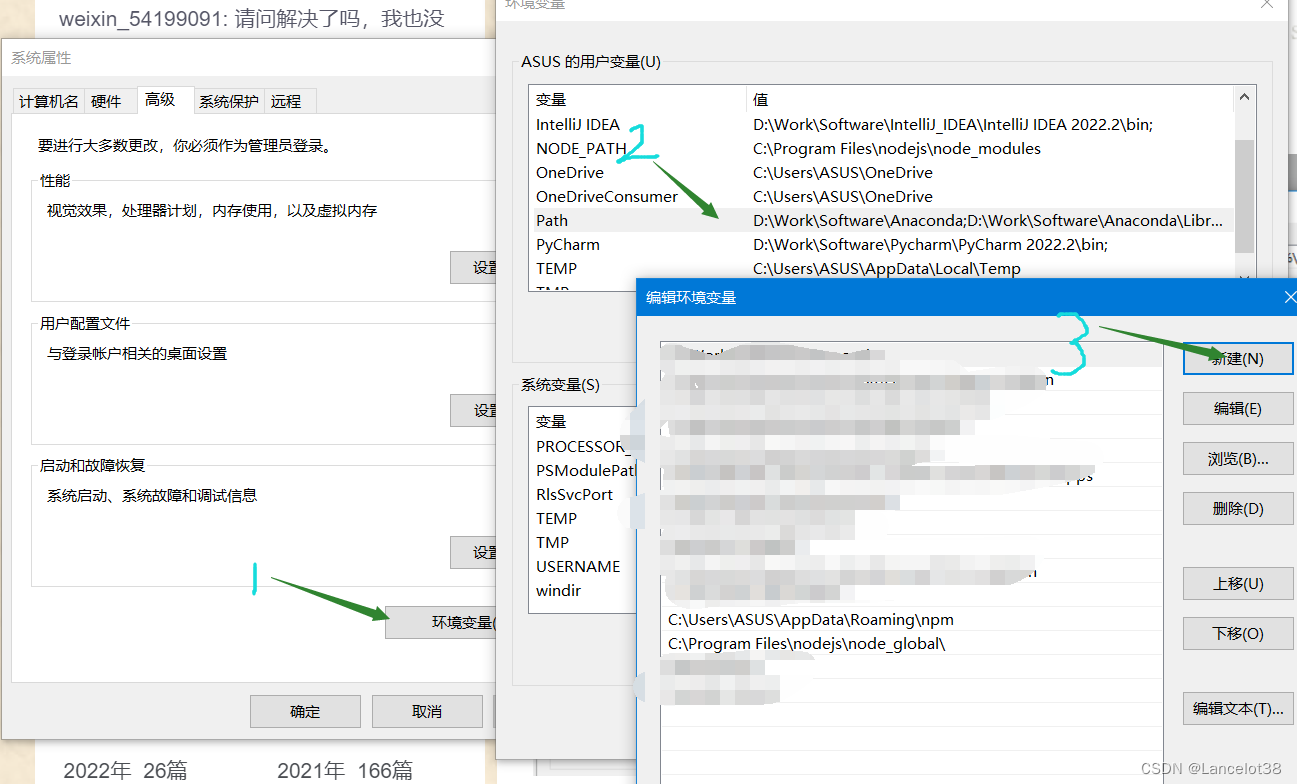
添加完成之后,即刻运行npm命令。
感谢你读到这里,相互学习,交流进步!!!