欧几里得定理、扩展欧几里德定义及中国剩余定理（数列和一些数学方面的概念）

article/2025/9/18 11:42:44

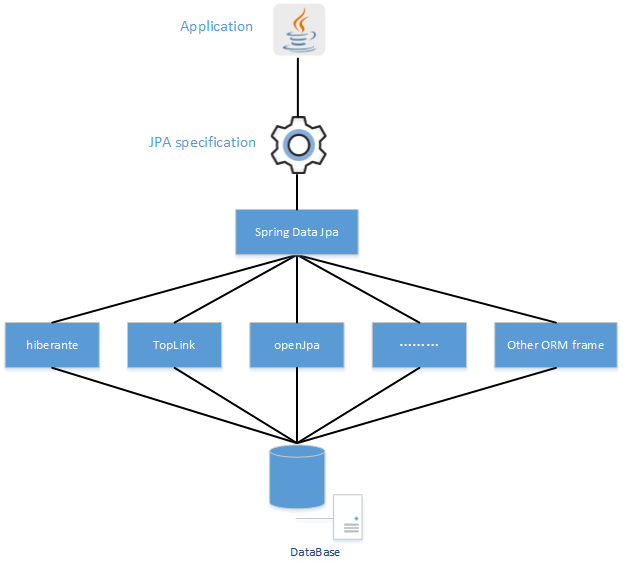
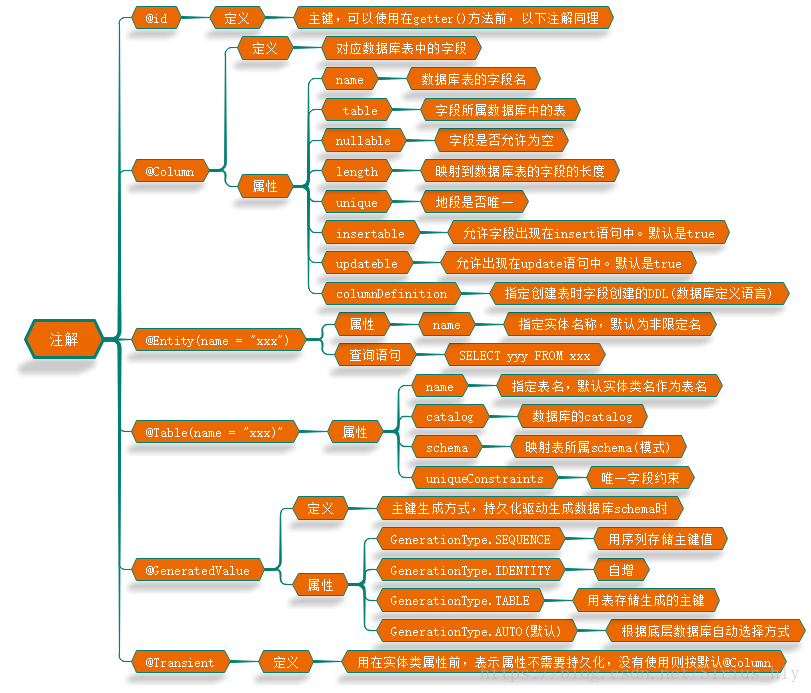
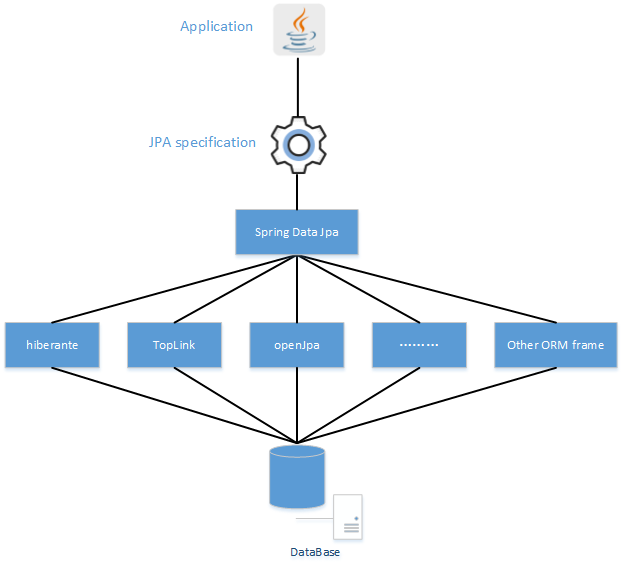
一、

欧几里得扩展：是欧几里得算法的扩展，已知整数a，b，扩展欧几里得算法可以在求得a，b的最大公约数的同时，能找到整数x、y（其中一个可能为负数），使得他们满足贝祖等式 $ax + by = gcd(a, b)$

如果a是负数，可以将问题转化为 $\left | a \right |(-x) + by = gcd(\left | a \right |,b)$

扩展欧几里得的几点应用：

可以用来求模逆元
可以用来求贝祖方程的解

令d = gcd（a，b）

贝祖定理：当且仅当m是d的倍数，关于未知数x和y的线性丢番图方程式ax + by = k有整数解

（这一定理是关于最大公约数的定理）

例如：14和42的最大公约数是6，则方程式12x + 42y = 6有解

特别的，对于ax + by = 1有整数解，当且仅当整数a和b互质

若已知a和b，求k的最小值，则min(k) = GCD（a, b)

扩展贝祖定理：如果给出一个这样的式子 y = a1 * x1 + a2 * x2 + a3 * x3 + ............... + ai * xi

求y的最小值，又该如何求解，同理求GCD（x1，x2，x3，x4，...........，xi）

ac代码：直接求最大公约数即可：

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<string>using namespace std;
typedef long long LL;const int maxn = 1e5+5;int n;
LL a[maxn];LL gcd(LL a, LL b){return b == 0?a:gcd(b, a%b);
}int main()
{scanf("%d", &n);for(int i = 0; i < n; i++) scanf("%lld", &a[i]);LL t = 0;for(int i = 0; i < n; i++){a[i] = abs(a[i]);if(t < a[i]) swap(t, a[i]);t = gcd(t, a[i]);}printf("%lld\n", t);return 0;
}

定理1：几个数相加，如果存在一个数不能被a整除，则他们的和也不能被a整除。

定理2：两数不能被整除，若除数扩大（缩小）几倍，被除数不变，则商和余数也同时扩大（缩小）相同的倍数。

对于贝祖方程ax + by = c，要是其有解，则GCD（a，b）能被c整除，否则无解。

求解不定方程的解：

#include<cstdio>
#include<iostream>
#include<algorithm>using namespace std;
typedef long long LL;LL exgcd(LL a, LL b, LL &x, LL &y){if(b == 0){x = 1;y = 0;return a;}LL g = exgcd(b, a%b, x, y);LL t = x;x = y;y = t - a/b*x;return g;
}int main()
{LL a, b, c, x, y;while(scanf("%lld%llld%lld", &a, &b, &c) != EOF){LL t = exgcd(a, b, x, y);if(x % t) printf("No solution\n");else{printf("%lld %lld\n", c/t*x, c/t*y);printf("%lld %lld\n", x, y);}}return 0;
}

参考：维基百科

https://blog.csdn.net/bigbigship/article/details/25073451

待续。。。。。

二、

中国剩余定理：用数学来表示，给出一个线性同余方程组：

$(S) : \quad \left\{ \begin{matrix} x \equiv a_1 \pmod {m_1} \\ x \equiv a_2 \pmod {m_2} \\ \vdots \qquad\qquad\qquad \\ x \equiv a_n \pmod {m_n} \end{matrix} \right.$