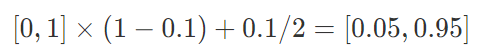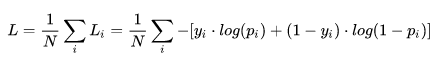指数平滑法 Exponential Smoothing

指数平滑法，用于中短期经济发展趋势预测。

1 时间序列分析基础知识

1.1 时间序列分析前提假设

时间序列分析一般假设我们获得的数据在时域上具有一定的相互依赖关系，例如股票价格在t时刻很高，那么在t+1时刻价格也会比较高（跌停才10%）；如果股票价格在一段时间内获得稳定的上升，那么在接下来的一段时间内延续上升趋势的概率也会比较大。

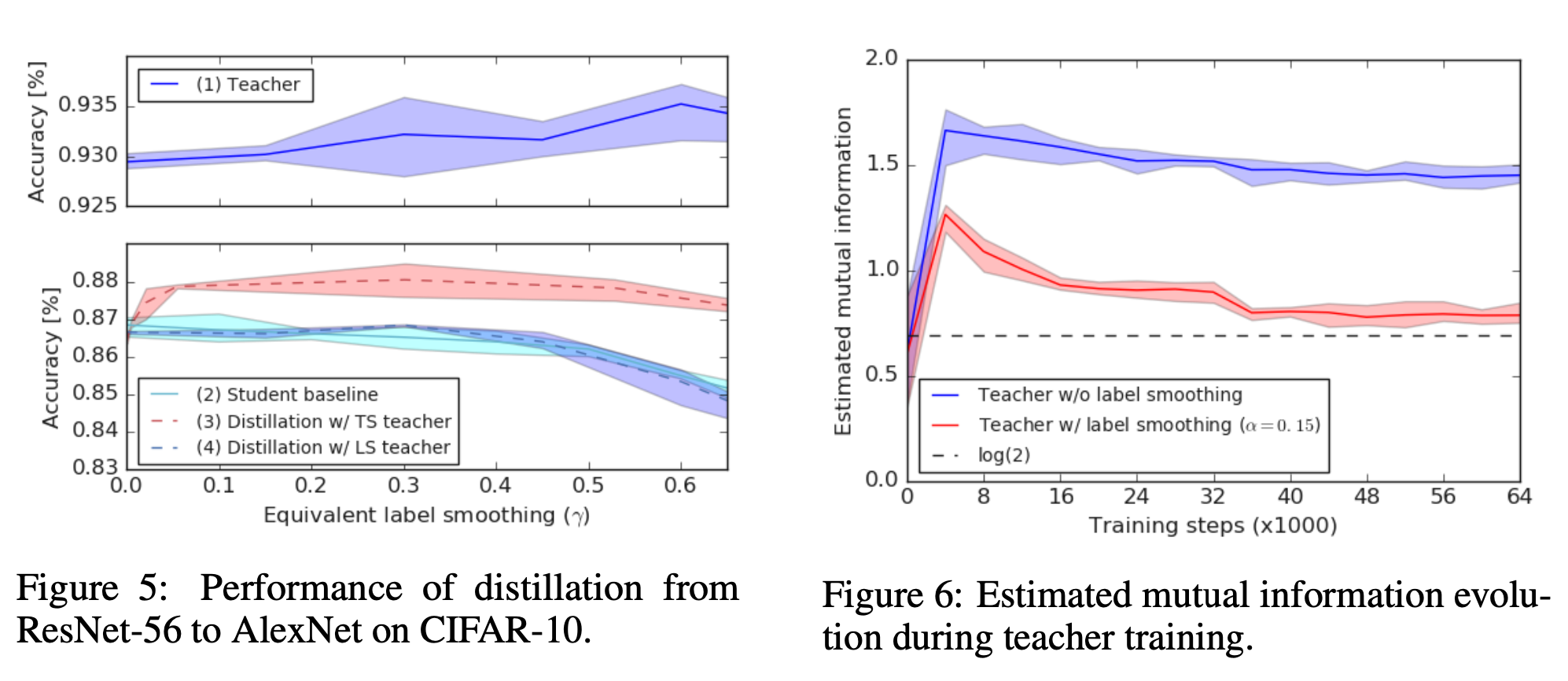
1.2 时间序列分析目标

（1）发现这种隐含的依赖关系，并增加我们对此类时间序列的理解；
（2）对未观测到的或者尚未发生的时间序列进行预测。
我们认为时间序列由两部分组成：有规律的时间序列（即有依赖关系）+噪声（无规律，无依赖）。所以，接下来要做的就是过滤噪声：

最简单的过滤噪声的方法是：取平均。

2 平均方法

• 全期平均法：简单的全期平均法是对时间数列的过去数据一个不漏地全部加以同等利用；
• 移动平均法：移动平均法则不考虑较远期的数据，并在加权移动平均法中给予近期资料更大的权重；（如ARIMA）
• 指数平滑法：指数平滑法则兼容了全期平均和移动平均所长，不舍弃过去的数据，但是仅给予逐渐减弱的影响程度，即随着数据的远离，赋予逐渐收敛为零的权数。

也就是说，指数平滑法是在移动平均法基础上发展起来的一种时间序列分析预测法，它是通过计算指数平滑值，配合一定的时间序列预测模型对现象的未来进行预测，其原理是任一期的指数平滑值都是本期实际观察值与前一期指数平滑值的加权平均。利用修匀技术，削弱短期随机波动对序列的影响，使序列平滑化，从而显示出长期趋势变化的规律。

用序列过去值的加权均值来预测将来的值，序列中近期的数据被赋以较大的权重，远期的数据被赋以较小的权重。理由是一般情况下，某一变量值对其后继行为的影响作用是逐渐衰减的。

3 指数平均(Exponential Smoothing/EXPMA)

指数平均方法的一个重要特征就是，S_t与之前产生的所有信号有关，并且距离越近的信号所占权重越大。

初始值的确定： 即第一期的预测值。一般原数列的项数较多时（大于15项），可以选用第一期的观察值或选用比第一期前一期的观察值作为初始值。如果原数列的项数较少时（小于15项），可以选取最初几期（一般为前三期）的平均数作为初始值。

指数平滑方法的选用： 一般可根据原数列散点图呈现的趋势来确定。如呈现直线趋势，选用二次指数平滑法；如呈现抛物线趋势，选用三次指数平滑法。或者，当时间序列的数据经二次指数平滑处理后，仍有曲率时，应用三次指数平滑法。

3.1 一阶指数平滑

当时间数列无明显的趋势变化，可用一次指数平滑预测。其预测公式为：
例题：已知某种产品最近15个月的销售量如下表所示：

用一次指数平滑值预测下个月的销售量y16。

为了分析加权系数a的不同取值的特点，分别取a=0.1,a=0.3,a=0.5计算一次指数平滑值，并设初始值为最早的三个数据的平均值，：以a = 0.5的一次指数平滑值计算为例，有

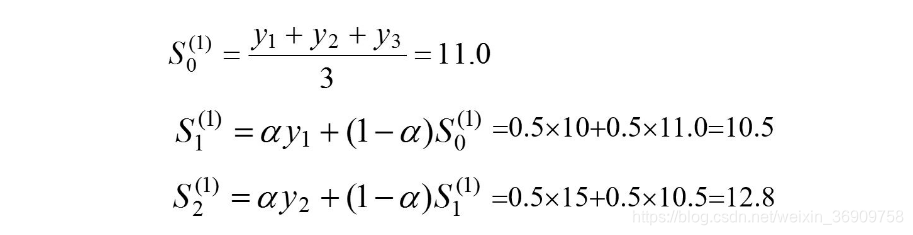
计算得到下表：

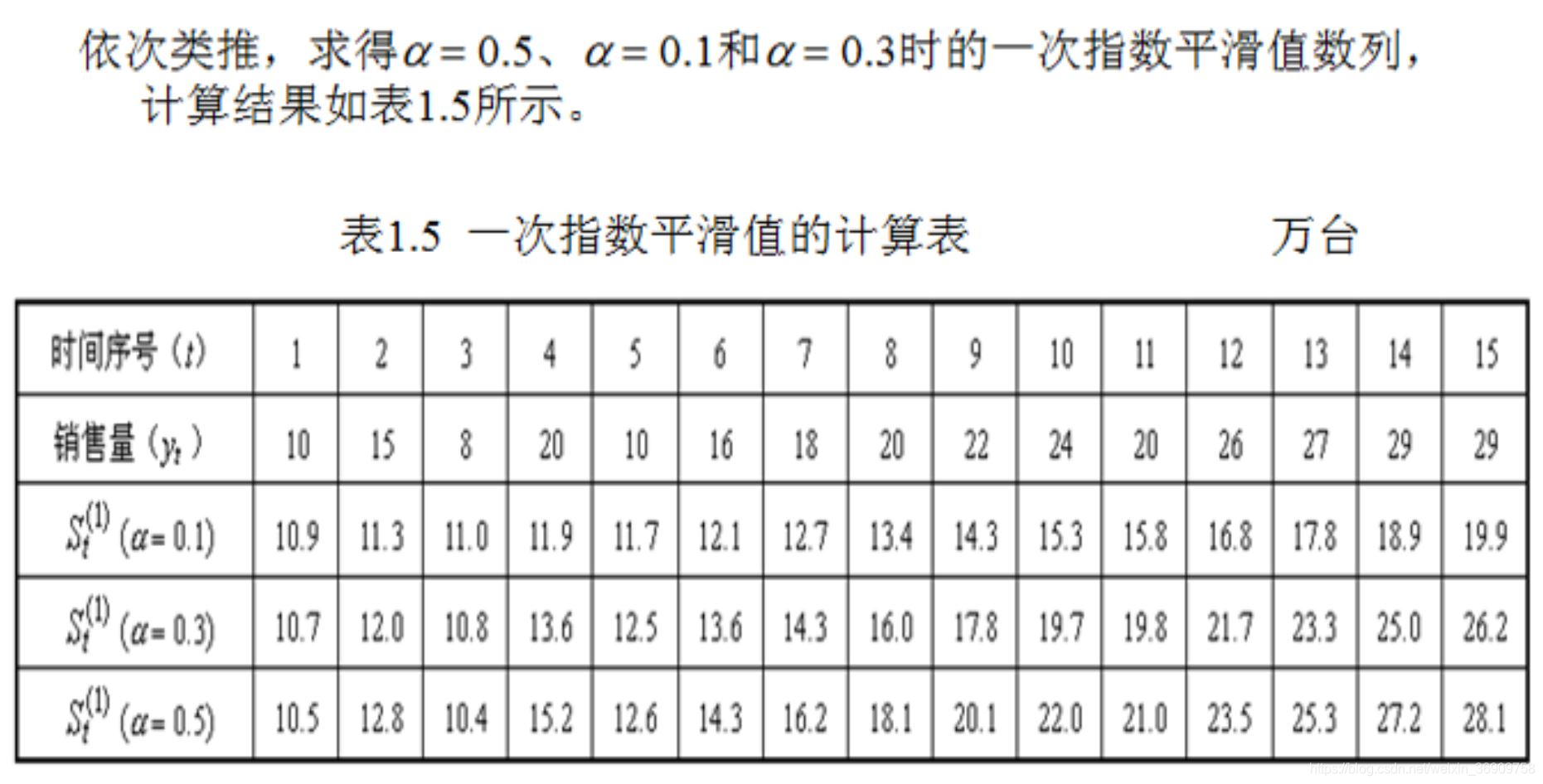
按上表可得 时间15月对应的19.9 26.2 28.1可以分别根据预测公式来预测第16个月的销售量。
以a = 0.5为例： y16=0.5*29+(1-0.5)*28.1=28.55（万台）

由上述例题可得结论

1. 最突出的优点：方法非常简单，甚至只要样本末期的平滑值，就可以得到预测结果。
2. 一次指数平滑有局限性：
   第一，预测值只考虑历史平均，不能反映趋势变动、季节波动等有规律的变动；
   第二，这种方法多适用于短期预测，而不适合作中长期的预测；
   第三，由于预测值是历史数据的均值，因此与实际序列的变化相比有滞后现象。修正的方法是在一次指数平滑的基础上再进行二次指数平滑，利用滞后偏差的规律找出曲线的发展方向和发展趋势，然后建立直线趋势预测模型，故称为二次指数平滑法。
3. 平滑系数：指数平滑预测是否理想，很大程度上取决于平滑系数。指数平滑法对实际序列具有平滑作用，平滑系数a 越小，平滑作用越强，但对实际数据的变动反应较迟缓。

3.2 二次指数平滑

二次指数平滑是对一次指数平滑的再平滑，同时考虑历史平均和变化趋势。它适用于具有线性趋势的时间数列。

我们可以看到，虽然一次指数平均在产生新的数列的时候考虑了所有的历史数据，但是仅仅考虑其静态值，即没有考虑时间序列当前的变化趋势。如果当前的股票处于上升趋势，那么当我们对明天的股票进行预测的时候，好的预测值不仅仅是对历史数据进行”平均“，而且要考虑到当前数据变化的上升趋势。同时考虑历史平均和变化趋势，这便是二阶指数平均。
在一次指数平滑的基础上得二次指数平滑 的计算公式为：

二次指数平滑法是对一次指数平滑值作再一次指数平滑的方法。它不能单独地进行预测，必须与一次指数平滑法配合，建立预测的数学模型，然后运用数学模型确定预测值。

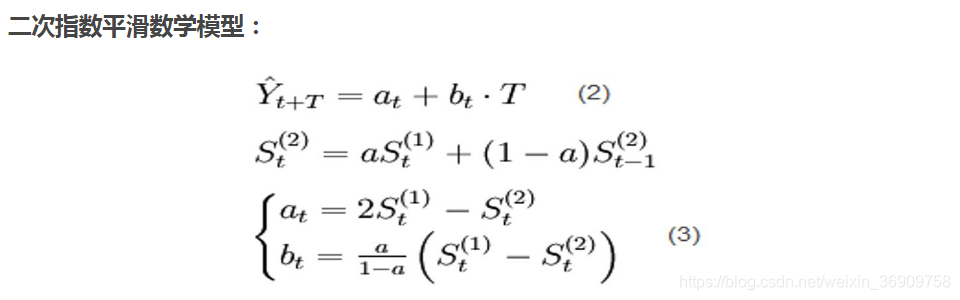
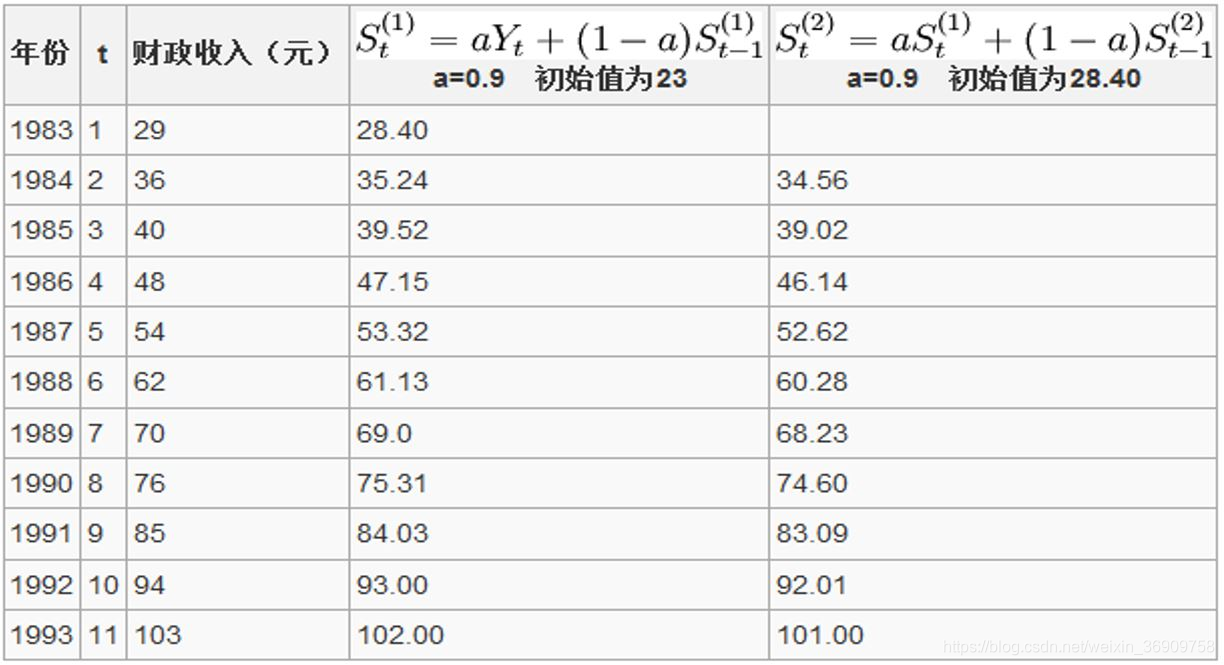
例题2：某地1983年至1993年财政入的资料如下，试用指数平滑法求解趋势直线方程并预测1996年的财政收入


3.3 三次指数平滑（Holt-Winters）

1. 与前两种相比，我们多考虑一个因素：季节性效应（ Seasonality）。这种平均模型考虑的季节性效应在股票或者期货价格中都会比较常见，比如在过年前A股市场通常会交易比较频繁，在小麦成熟的时候小麦期货价格也会有比较明显的波动。但是，模型本身的复杂度也增加了其使用难度，我们需要一定的经验才能比较合理地设置其中复杂的参数。
2. 若时间序列的变动呈现出二次曲线趋势，则需要采用三次指数平滑法进行预测。三次指数平滑是在二次指数平滑的基础上再进行一次平滑，其计算公式为：
   
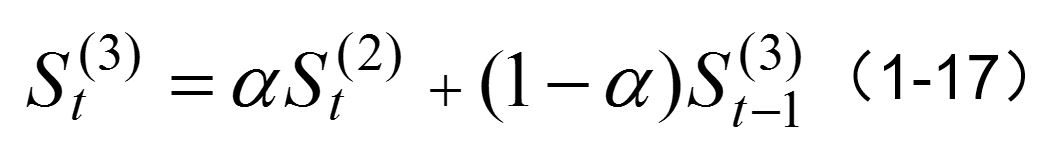
   三次指数平滑法的预测模型为：
   
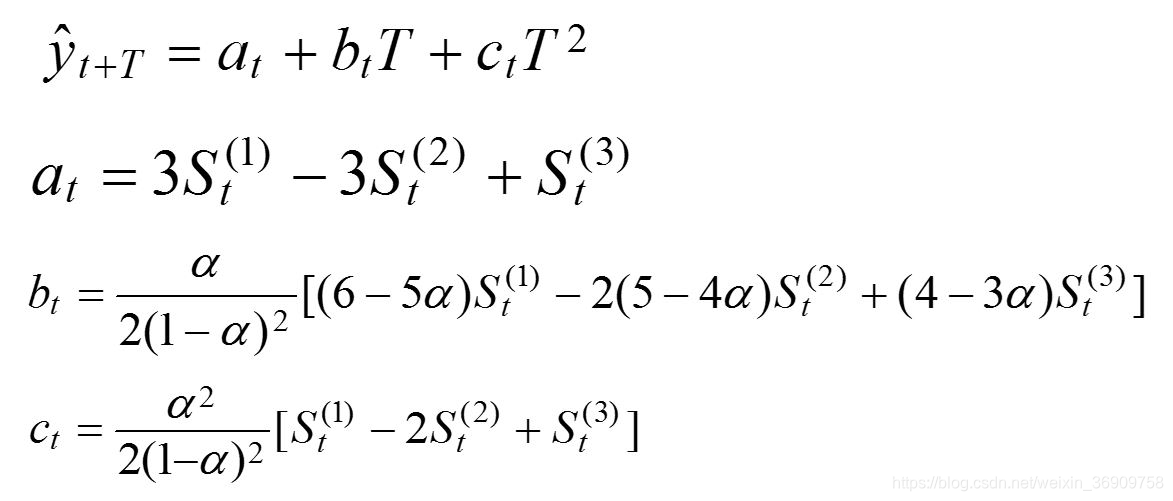
   例4：我国某种耐用消费品1996年至2006年的销售量如表所示，试预测2007、2008年的销售量。
   三次指数平滑的计算表：
   解：通过实际数据序列呈非线性递增趋势，采用三次指数平滑预测方法。解题步骤如下。确定指数平滑的初始值和权系数（平滑系数）a。设一次、二次指数平滑的初始值为最早三个数据的平均值，即
   
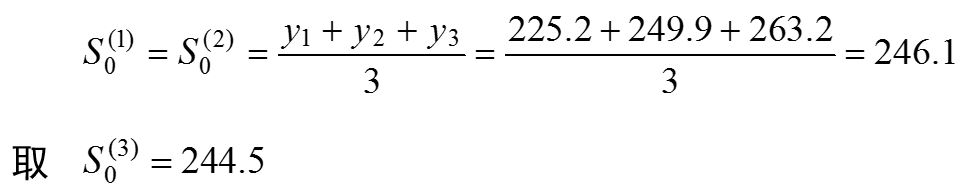
   实际数据序列的倾向性变动较明显，权系数（平滑系数）a 不宜取太小，故取a= 0.3。
   根据指数平滑值计算公式依次计算一次、二次、三次指数平滑值：
   
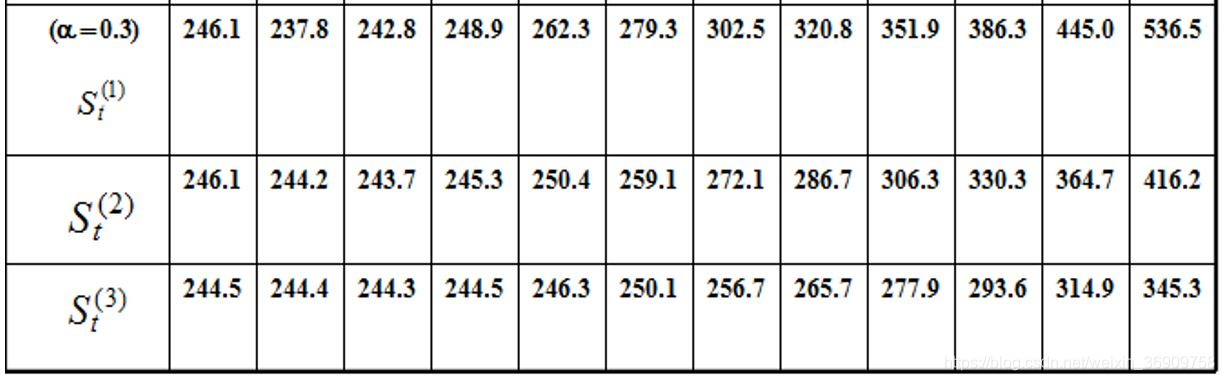
   计算非线性预测模型的系数at,bt,ct。目前周期数t = 11，将表1.6中的有关数据代入式（1-19）、式（1-20）、式（1-21）后分别得
   
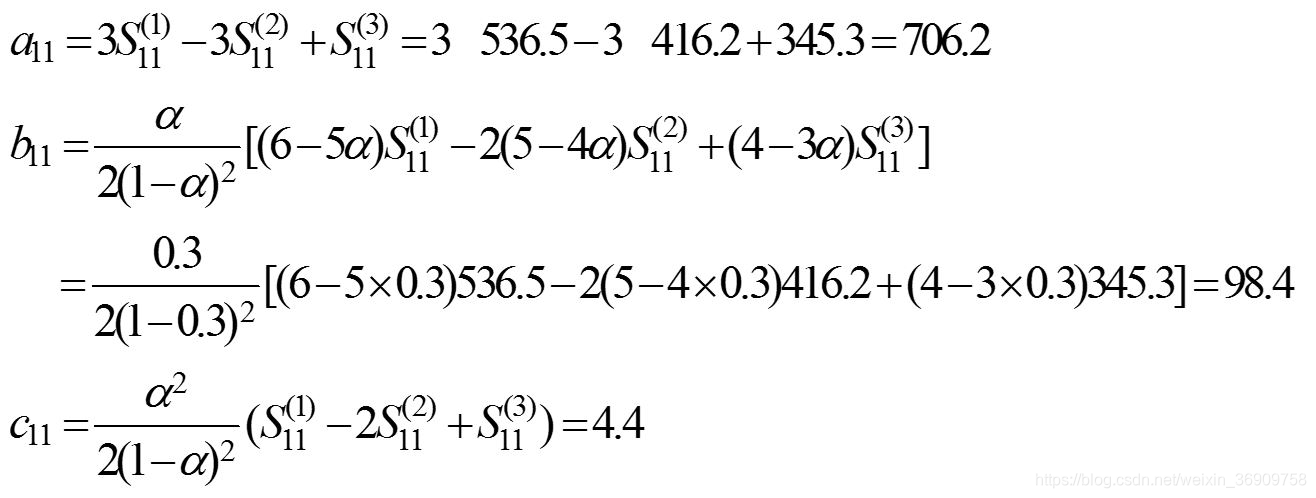
   建立非线性预测模型。将各系数代入式（1-18）得
   
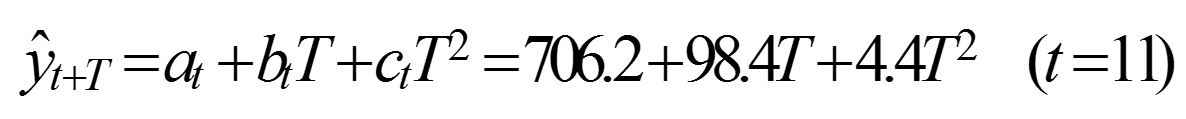
   预测2007年和2008年的产品销售量。2007年，其预测超前周期为T = 1；2008年，其预测超前周期为T = 2。代入模型，得预测2007年和2008年的产品销售量。2007年，其预测超前周期为T= 1；2008年，其预测超前周期为T= 2。代入模型，得
   
   于是得到2007年的产品销售量的预测值为809万台，2008年的产品销售量的预测值为920万台。预测人员可以根据市场需求因素的变动情况，对上述预测结果进行评价和修正。

4 总结

1.基本思想：预测值是以前观测值的加权和，且对不同的数据给予不同的权，新数据给较大的权，旧数据给较小的权。
2.方法选择
一次指数平滑法：针对没有趋势和季节性的序列
二次指数平滑法：针对有趋势但没有季节性的序列
三次指数平滑法：针对有趋势也有季节性的序列。“Holt-Winters”有时特指三次指数平滑法。
3.指数平滑法的优缺点

• 优点：
  （1）对不同时间的数据的非等权处理较符合实际情况。
  （2）实用中仅需选择一个模型参数a 即可进行预测，简便易行。
  （3）具有适应性，也就是说预测模型能自动识别数据模式的变化而加以调整。
• 缺点：
  （1）对数据的转折点缺乏鉴别能力，但这一点可通过调查预测法或专家预测法加以弥补。
  （2）长期预测的效果较差，故多用于短期预测。

参考

1.Holt-Winters版本公式：https://blog.csdn.net/anshuai_aw1/article/details/82499095
2.https://blog.csdn.net/weixin_40396948/article/details/79108469
3.https://blog.csdn.net/qq_27586341/article/details/90906104