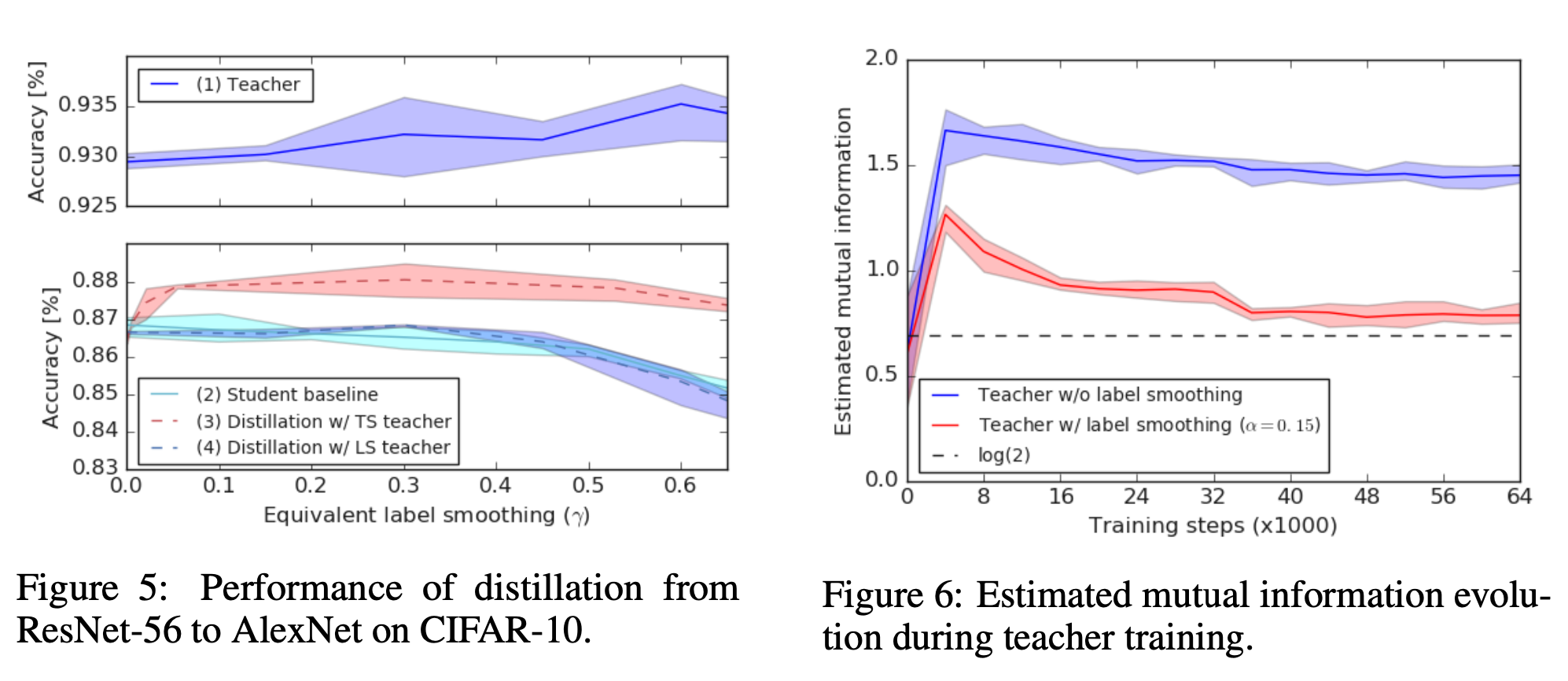
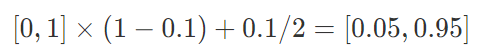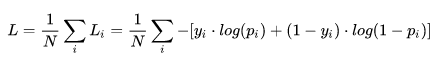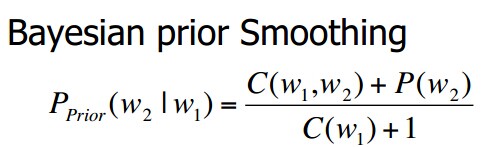label smoothing是一种在分类问题中，防止过拟合的方法。

交叉熵损失函数在多分类任务中存在的问题

多分类任务中，神经网络会输出一个当前数据对应于各个类别的置信度分数，将这些分数通过softmax进行归一化处理，最终会得到当前数据属于每个类别的概率。

$$q_i=\frac{exp(z_i)}{{\sum }_{j=1}^{k}exp(z_j)}$$

然后计算交叉熵损失函数：

$$Loss=-\sum _{i=1}^k{p}_{i}log{q}_i$$

$$p_i=\{\begin{array}{c}1,if(i=y)\\ 0,if(i\ne y)\end{array}$$

$$其中i表示多分类中的某一类$$

训练神经网络时，最小化预测概率和标签真实概率之间的交叉熵，从而得到最优的预测概率分布。最优的预测概率分布是：

$$Z_i=\{\begin{array}{c}+\infty ,if(i=y)\\ 0,if(i\ne y)\end{array}$$

神经网络会促使自身往正确标签和错误标签差值最大的方向学习，在训练数据较少，不足以表征所有的样本特征的情况下，会导致网络过拟合。

label smoothing（标签平滑）

label smoothing可以解决上述问题，这是一种正则化策略，主要通过soft one-hot来加入噪声，减少真实样本标签的类别在计算损失函数时的权重，最终起到抑制过拟合的效果。
增加label smoothing后真实的概率分布有如下改变：

$$p_i=\{\begin{array}{c}1,if(i=y)\\ 0,if(i\ne y)\end{array}$$

$$p_i=\{\begin{array}{c}(1-ϵ),if(i=y)\\ \frac{ϵ}{K-1},if(i\ne y)\end{array}$$

$$K表示多分类的类别总数$$
$$ϵ是一个较小的超参数$$

交叉熵损失函数的改变如下：

$$Loss=-\sum _{i=1}^k{p}_{i}log{q}_i$$

$$Loss=\{\begin{array}{c}(1-ϵ)\ast Loss,if(i=y)\\ ϵ\ast Loss,if(i\ne y)\end{array}$$

最优预测概率分布如下：

$$Z_i=\{\begin{array}{c}+\infty ,if(i=y)\\ 0,if(i\ne y)\end{array}$$

$$Z_i=\{\begin{array}{c}log\frac{(k-1)(1-ϵ)}{ϵ+\alpha },if(i=y)\\ \alpha ,if(i\ne y)\end{array}$$

这里的α是任意实数，最终模型通过抑制正负样本输出差值，使得网络有更强的泛化能力。

参考资料

1. https://zhuanlan.zhihu.com/p/116466239
2. https://blog.csdn.net/qq_43211132/article/details/100510113