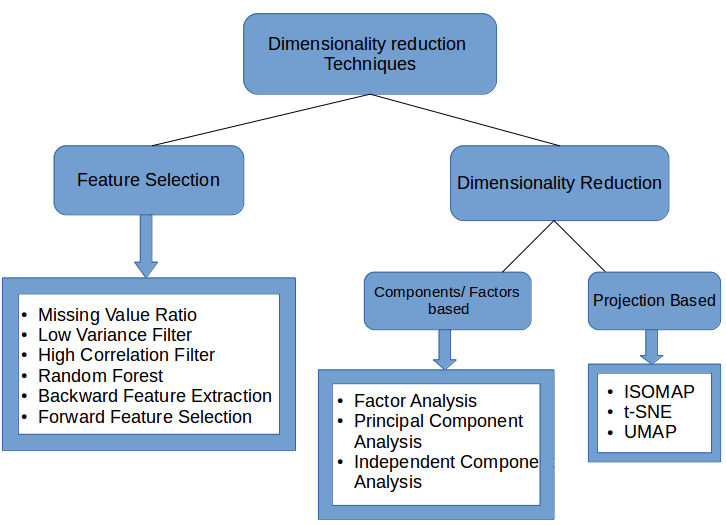
目录
一、主成分分析
二、奇异值分解
2.1 奇异值分解原理
2.2 奇异值分解实践
三、特征值与特征向量
一、主成分分析
主成分有如下特征:
- 每个主成分是原变量的线性组合;
- 各个主成分之间互不相关;
- 主成分按照方差贡献率从大到小依次排列;
- 所有主成分的方差贡献率求和为1;
- 提取后的主成分通常小于原始数据变量的数量;
- 提取后的主成分尽可能地保留了原始变量中的大部分信息。
我们仍以经典的鸢尾花数据集对主成分分析进行介绍。
通过导入PCA进行主成分分析。
#导入库
import numpy as np
import pandas as pd
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris#导入数据
data=load_iris()#主成分分析
model=PCA()
model.fit(data.data)#显示主成分信息
pd.DataFrame(model.transform(data.data),columns=["PC{}".format(x+1) for x in range(data.data.shape[1])])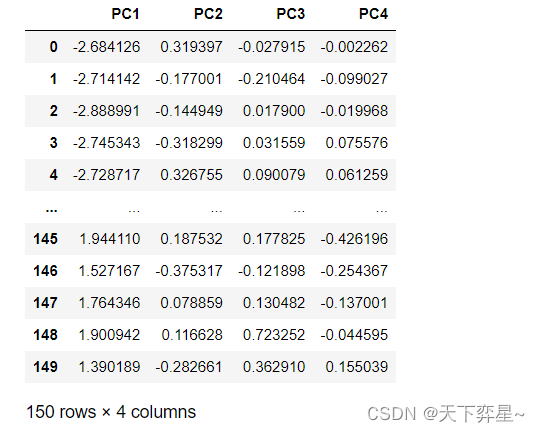
上述结果给出了鸢尾花数据集的4个(全部)主成分,然而选择几个主成分需要进一步判断。这里可以通过计算主成分的累计贡献率进行判断,代码如下:
import matplotlib.ticker as ticker
import matplotlib.pyplot as plt
plt.gca().get_xaxis().set_major_locator(ticker.MaxNLocator(integer=True))
plt.plot([0]+list(np.cumsum(model.explained_variance_ratio_)),"-")
plt.xlabel("Number of principal componets")
plt.ylabel("Cumulative contribution rate")
plt.show()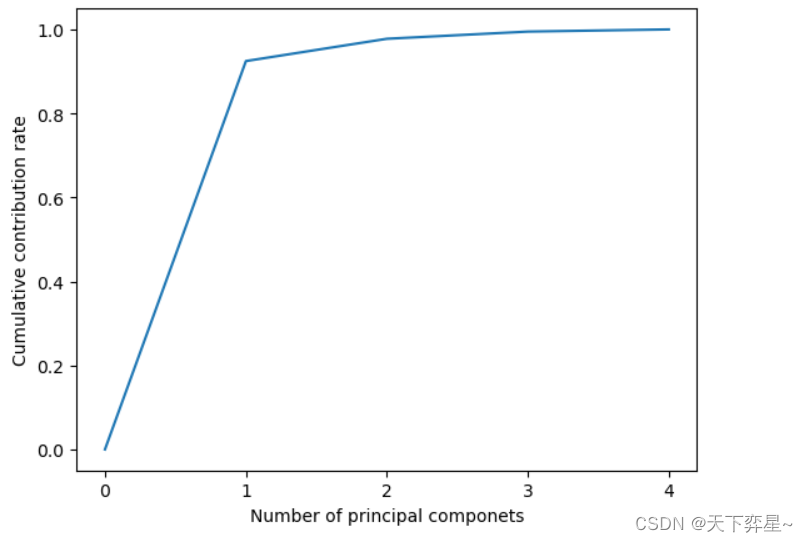
从上图可以看出,主成分从0~1时非常陡峭,而从1往后区域平缓,因此,针对4维鸢尾花数据,我们只需要保留1个主成分,即将原4维数据降维到现在的1维。
利用下面的代码,我们可以用更加量化的方式查看主成分累积贡献率。
model.explained_variance_ratio_![]()
结果显示,1个主成分就已经达到了92.46%,保留了原数据中绝大部分信息。
综上,主成分分析的全部代码如下:
#导入库
import numpy as np
import pandas as pd
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris#导入数据
data=load_iris()#主成分分析
model=PCA()
model.fit(data.data)#显示主成分信息
pd.DataFrame(model.transform(data.data),columns=["PC{}".format(x+1) for x in range(data.data.shape[1])])#绘制主成分的累积贡献率的折线图
import matplotlib.ticker as ticker
import matplotlib.pyplot as plt
plt.gca().get_xaxis().set_major_locator(ticker.MaxNLocator(integer=True))
plt.plot([0]+list(np.cumsum(model.explained_variance_ratio_)),"-")
plt.xlabel("Number of principal componets")
plt.ylabel("Cumulative contribution rate")
plt.show()#量化主成分的累计贡献率
model.explained_variance_ratio_二、奇异值分解
2.1 奇异值分解原理
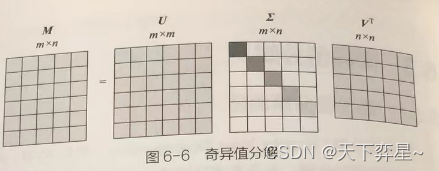
奇异值分解(SVD)将一个任意矩阵进行分解,无须考虑特征值分解时需要矩阵是方阵的前提。
假设矩阵M是一个阶矩阵,则可以将其分解为下面的三个矩阵相乘:
其中:
- U是
阶正交矩阵,
,
为单位矩阵;
是
阶正交矩阵,
;
是
阶非负实数对角矩阵,
。
这种将矩阵M分解的方法就被称为奇异值分解,矩阵上对角线上的元素即为M的奇异值。
考虑一个的任意矩阵,此时
的秩为n,矩阵中不同深度的灰色表示奇异值大小不同,对角线上的奇异值(假设存在n个非零的奇异值)依次从大到小进行排列。在这种情况下,矩阵U的最后m-n列失去了意义。
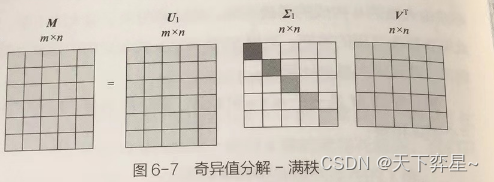
因此可以做进一步的变化,此时阶的矩阵U变为
阶的矩阵
,
阶的矩阵
变为
阶的矩阵
。
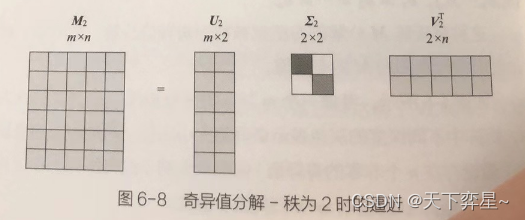
当我们取k<n,比如k=2时,即认为前两个奇异值占总奇异值之和的比例非常大,因此可以如下图进行运算,尽管此时,但是由于删除的奇异值占比很小,我们可以认为
。
2.2 奇异值分解实践
利用python可以很方便实现对矩阵的奇异值分解,例如对阶的矩阵M进行奇异值分解:
代码如下:
import numpy as np
M=np.array([[1,0,0,0,2],[0,0,3,0,0],[0,0,0,0,0],[0,4,0,0,0]])
U,Sigma,VT=np.linalg.svd(M)
print("U:",U)
print("Sigma:",Sigma)
print("VT:",VT)
导入一张图片,下面的代码给出了地秩近似序列使用奇异值分解逼近的图片。
import numpy as np
import matplotlib.pyplot as plt
from PIL import Imager_max=300 #设置最大的秩
Pic="C:\\Users\\LEGION\\Pictures\\Saved Pictures\\暨大logo.png"image=Image.open(Pic).convert("L")
img_mat=np.asarray(image)U,s,V=np.linalg.svd(img_mat,full_matrices=True)
s=np.diag(s)for k in range(r_max+1):approx=U[:,:k] @ s[0:k,:k] @ V[:k,:]img=plt.imshow(approx,cmap='gray')plt.title("SVD approximation with degree of %d"%(k))plt.plot()plt.pause(0.001)plt.clf()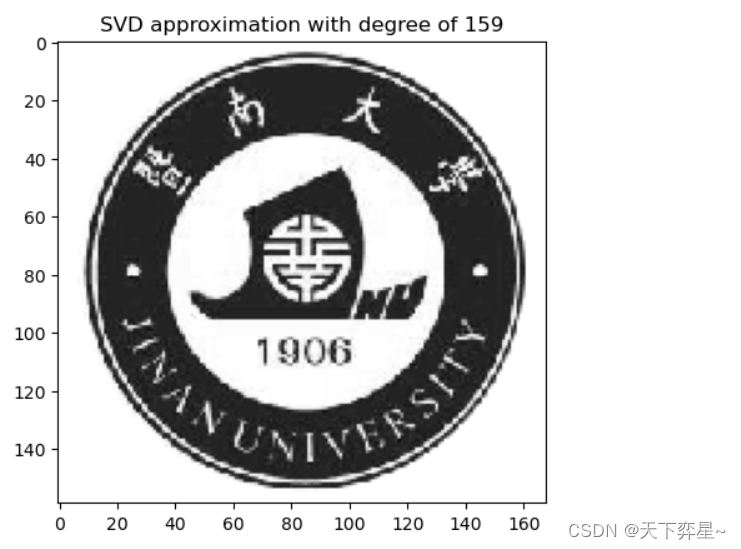
三、特征值与特征向量
利用python与Numpy库,很容易得到一个矩阵的特征值和特征向量。
import numpy as np
A=np.array([[1,2],[3,4]])
a,b=np.linalg.eig(A)
print("A的特征值为:\n",a)
print('A的特征向量为:\n',b) 
通过np.lianlg.eig()函数得到的特征向量是已经标准化的向量, 即长度为1.改函数给出的特征值未按大小顺序排序。
除了特征值和特征向量外,协方差矩阵与相关系数矩阵也是降维分析中的重要概念。以鸢尾花的4个特征向量为例,协方差矩阵的每个元素是各个向量元素之间的协方差,相关系数矩阵的各元素是由各特征间的相关系数构成的。
import numpy as np
from sklearn.datasets import load_iris#导入数
data=load_iris()
X=data.dataCov_X=np.cov(X.T) #求解协方差矩阵
Cor_X=np.corrcoef(X.T) #求解相关系数矩阵print("协方差矩阵:\n",Cov_X)
print("相关系数矩阵:\n",Cor_X)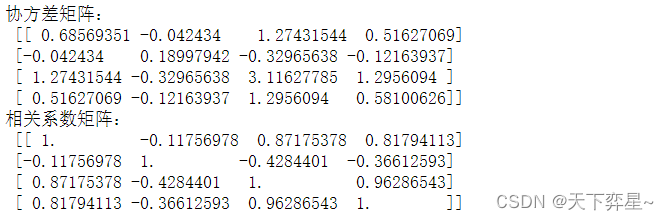
利用协方差矩阵和相关系数矩阵可以求解主成分。这里以利用协方差矩阵为例进行说明。
沿用上面的协方差矩阵数据,可以求得其特征值和特征向量:
import numpy as np
from sklearn.datasets import load_iris#导入数
data=load_iris()
X=data.dataCov_X=np.cov(X.T) #求解协方差矩阵a,b=np.linalg.eig(Cov_X)
print("协方差矩阵的特征值为:\n",a)
print('协方差矩阵的特征向量为:\n',b)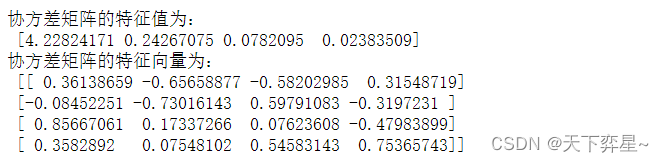
协方差矩阵的特征值即为主成分的方差贡献率:
第一个主成分(解释方差)所占比例已经高达92.46%,说明已经可以在这个比例上解释原始数据信息,因此可以将鸢尾花数据从四维降至一维。第一主成分如下:
其中,表示该列特征的均值,等式右边的系数为协方差矩阵的特征向量的第一列(与第一个特征值相对应的数值)。
除了协方差矩阵,相关系数矩阵也可以求解主成分。但是两种不同的求解方法结果通常会有一定的差别。此外,值得注意的是,如果对已经标准化的数据求协方差矩阵,实际上就是对原变量求相关系数矩阵。
在求解主成分时,如果变量间的单位不同,应该先将变量标准化后进行计算。否则由于单位不同导致的取值范围悬殊太大会影响最终的结果。