鄙人不才,在学校的时候没有学python,复合材料力学也是一知半解,后来工作的时候遇到了需要计算复合材料层合板ABD刚度矩阵的内容,然后恰好在学习python,于是花时间编写了下预测这方面的内容,然后后期还编写了通过Tsai-Wu,Tsai-Hill失效准则预测层合板强度的模块,不过代码编的比较烂,后期会学习python项目管理,然后封装好。
备注:由于本人代码水平有限,现有代码还需要更改,主要是模块间的数据读入和数据传递比较混乱,但模块的计算能力没有问题,各位观众老爷在学习的时候可以参考《复合材料力学》相关书籍的经典层合板理论对照阅读。
@Time : 2018-12-28
@Author : Allen Pen
@E-mail : shengyutou@outlook.com
目录
- 理论部分
- 复合材料基础理论
- 单层板的宏观力学分析
- 层合板的宏观力学分析
- 单层板的细观力学分析
- 计算逻辑与实现逻辑
- 计算逻辑
- 层合板ABD刚度矩阵计算
- 层合板强度预测
- 最后的最后
# 文件读取 这里需要进行数据读入操作,可以通过GUI填入,或者是读取.txt文档。或者是通过细观力学计算得来。
理论部分
待更新。
复合材料基础理论
待更新。
单层板的宏观力学分析
层合板的宏观力学分析
单层板的细观力学分析
待更新。
计算逻辑与实现逻辑
计算逻辑
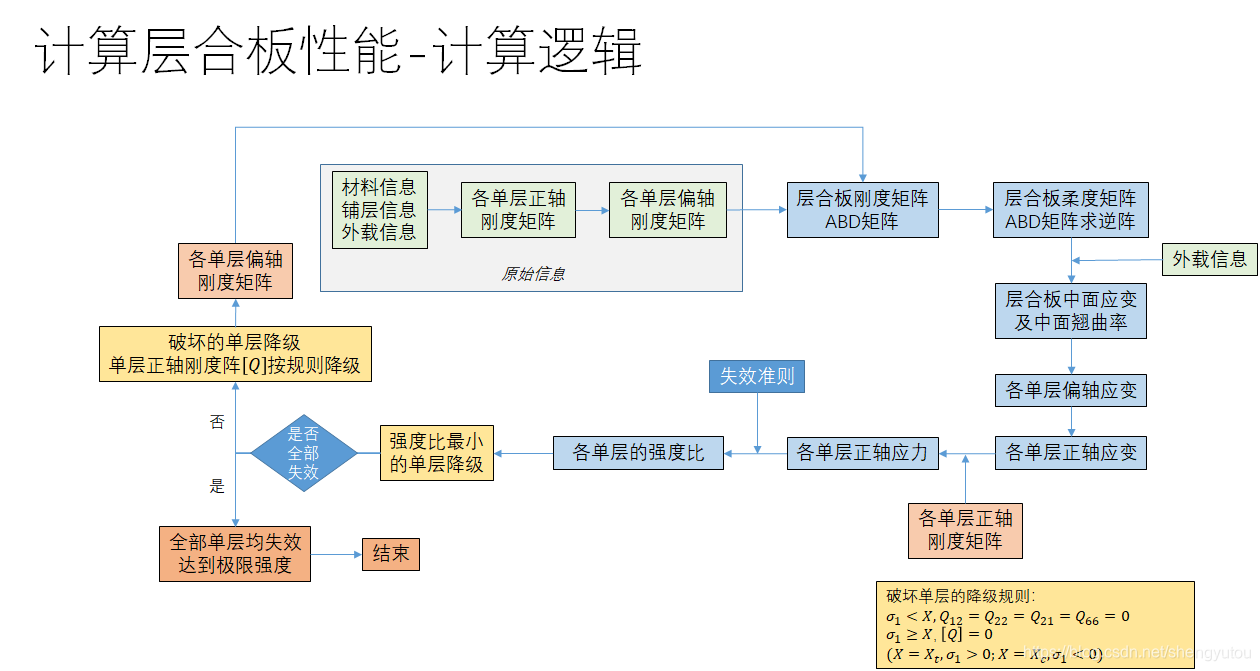
# 计算单层板弹性常数
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time : 2018-12-28
# @Author : Allen Pen
# @E-mail : shengyutou@outlook.comimport numpy as np
import numpy.linalg as lg
from CLPTC.calculator.input_file_reader import ply_properties,mat_propertiesclass Lamina():'''注意:正轴 -- 与铺层纤维方向相同的方向为正轴向,以1,2,3方向表示偏轴 -- 一般为层合板自然轴定义的坐标系,以x,y,z表示,相对于铺层的坐标系铺层角 -- 偏轴x转至正轴1的夹角,逆时针转向为正泊松比 -- 泊松比使用国外的书和软件的定义方式,即ν_12=-ε_2/ε_1 ,ν_21=-ε_1/ε_2使用nu12,nu12(OptiStruct) = nuxy(ANSYS) = ν_12(国外教材)=ν_1(复合材料力学)=ν_21(复合材料力学)=-ε_2/ε_1matid material ide1 Young Modulus in direction 1e2 Young Modulus in direction 2g12 in-plane shear modulusnu21 Poisson's ratio 21,nu21=-ε2/ε1nu12 Poisson's ratio 12: use formula nu21/e1 = nu12/e2st1,st2 allowable tensile stresses for directions 1 and 2sc1,sc2 allowable compressive stresses for directions 1 and 2ss12 allowable in-plane stress for shearstrn allowable strain for direction 1plyid id of the composite laminat ply thicknesstheta ply angleS (单层的)正轴柔量矩阵Q (单层的)正轴模量矩阵T_stress 应力转换矩阵T_strain 应变转换矩阵S_offaxis (单层的)偏轴柔量矩阵Q_offaxis (单层的)偏轴模量矩阵Sij compliance component 柔量分量Qij modulus component 模量分量'''def __init__(self):self.matid = Noneself.plyid = Noneself.t = Noneself.theta = Noneself.e1 = Noneself.e2 = Noneself.g12 = Noneself.nu21 = Noneself.nu12 = Noneself.st1 = Noneself.st2 = Noneself.sc1 = Noneself.sc2 = Noneself.ss12 = Noneself.strn = Noneself.S = Noneself.Q = Noneself.T_stress = Noneself.T_strain = Noneself.S_offaxis= Noneself.Q_offaxis= Noneself.lamina_Ex = Noneself.lamina_Ey = Noneself.lamina_Gxy = Noneself.lamina_nuxy= Noneself.laminates= []self.cos = Noneself.cos2t = Noneself.sin = Noneself.sin2t = Nonedef calc_SQ(self):'''计算单层的正轴刚度:return: 只返回 S、Q,中间的s11等变量无法访问'''e1 = self.e1e2 = self.e2nu21 = self.nu21nu12 = self.nu12g12 = self.g12s11 = 1 / e1s22 = 1 / e2s66 = 1 / g12s12 = -nu12 / e2s21 = -nu21 / e1s16 = s61 = s26 = s62 = 0qm = (1 - nu21*nu12)q11 = e1/qmq22 = e2/qmq66 = g12q12 = nu12 * e1/qmq21 = nu21 * e2/qmq16 = q61 = q26 = q62 = 0self.S = np.array([[s11,s12,s16],[s21,s22,s26],[s61,s62,s66]],dtype = float)self.Q = np.array([[q11,q12,q16],[q21,q22,q26],[q61,q62,q66]],dtype = float)# 计算各单层的偏轴刚度theta = self.thetaself.cos = np.cos( np.deg2rad( theta ) )self.sin = np.sin( np.deg2rad( theta ) )# self.cos2t = np.cos( np.deg2rad( 2*self.theta ) )# self.sin2t = np.sin( np.deg2rad( 2*self.theta ) )cos = self.cossin = self.sincos2 = cos**2sin2 = sin**2sincos = sin*cos# cos2t = self.cos2t# sin2t = self.sin2t# 应力转换矩阵,用于将偏轴应力转换至正轴应力self.T_stress = np.array([[ cos2, sin2, 2*sincos],[ sin2, cos2, -2*sincos],[-sincos,sincos, cos2-sin2]],dtype=float)# 应变转换矩阵,用于将偏轴应变转换至正轴应变self.T_strain = np.array([[ cos2, sin2, sincos],[ sin2, cos2, -sincos],[-2*sincos,2*sincos, cos2-sin2]],dtype=float)# 计算偏轴刚度矩阵self.Q_offaxis = np.dot(np.dot(lg.inv(self.T_stress), self.Q), self.T_strain)self.S_offaxis = np.dot(np.dot(lg.inv(self.T_strain), self.S), self.T_stress)# 铺层等效的工程弹性常数self.lamina_Ex = 1/self.S_offaxis[0,0]self.lamina_Ey = 1/self.S_offaxis[1,1]self.lamina_Gxy = 1/self.S_offaxis[2,2]self.lamina_nuxy= -self.lamina_Ex*self.S_offaxis[0,1]def Get_lamina_prop(plyid):lamina_prop = Lamina()#铺层属性lamina_prop.matid = ply_properties['材料索引值'][plyid]lamina_prop.t = ply_properties['厚度'][plyid]lamina_prop.theta = ply_properties['铺层角'][plyid]# 铺层的材料属性lamina_prop.e1 = mat_properties['E1'][lamina_prop.matid]lamina_prop.e2 = mat_properties['E2'][lamina_prop.matid]lamina_prop.nu21 = mat_properties['nu21'][lamina_prop.matid]lamina_prop.g12 = mat_properties['G12'][lamina_prop.matid]lamina_prop.nu12 = lamina_prop.nu21/lamina_prop.e1*lamina_prop.e2lamina_prop.calc_SQ()return lamina_prop层合板ABD刚度矩阵计算
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time : 2018-12-28
# @Author : Allen Penimport numpy as np
import numpy.linalg as lg
import matplotlib.pyplot as plt
from CLPTC.calculator.lamina import Get_lamina_prop #从
from CLPTC.calculator.input_file_reader import total_ply_num,z_coord_dict,z_total,load_info,ply_properties,mat_propertiesclass Laminate():"""equiv_e1 equivalent laminate modulus in 1 directionequiv_e2 equivalent laminate modulus in 2 directionequiv_g12 equivalent laminate shear modulus in 12 directionequiv_nu21 equivalent laminate Poisson ratio in 21 directionequiv_nu12 equivalent laminate Poisson ratio in 12 directionplyid id of the composite laminaplies list of pliesplyts ply thicknesses for this laminatet total thickness of the laminateA 面内刚度系数矩阵B 耦合刚度系数矩阵D 弯曲刚度系数矩阵ABD ABD刚度矩阵用于计算柔度矩阵的中间变量A_temp = A^-1B_temp = -A^-1*BH_temp = B*A^-1D_temp = -B*A^-1*B+DA_inverted 面内柔度系数矩阵B_inverted 耦合柔度系数矩阵H_inverted 一般情况下 H_inverted = B_invertedD_inverted 弯曲柔度系数矩阵ABHD_inverted ABD柔度矩阵epsilon_0 板中面应变K 板中面翘曲率"""def __init__(self):self.plyid= Noneself.plies= Noneself.plyts= Noneself.t = Noneself.equiv_e1 = Noneself.equiv_e2 = Noneself.equiv_g12 = Noneself.equiv_nu21 = Noneself.equiv_nu12 = Noneself.A = Noneself.B = Noneself.D = Noneself.ABD = Noneself.A_temp = Noneself.B_temp = Noneself.H_temp = Noneself.D_temp = Noneself.A_inverted = Noneself.B_inverted = Noneself.H_inverted = Noneself.D_inverted = Noneself.ABHD_inverted = Noneself.epsilon_K_offaxis = Noneself.epsilon_offaxis_0 = None #板中面应变self.K = None #板中面翘曲率self.load_info = None #用于在最大强度比小于1的情况下更新载荷self.N_M = None #层合板当前能承受的载荷self.count = 0 #用于层合板失效层数的统计_ = self.init_build() #在类实例化时,将ABD 刚度阵、柔度阵,以及层的应变计算出来# 设置np数组输出的精度,注意,数组依然按float64储存np.set_printoptions(formatter={'float': '{: 10.3f}'.format})def calc_ABD(self):"""用于计算A,B,D刚度矩阵,以及A',B',D'柔度矩阵ref. 沈观林.《复合材料力学》:return:ABD A,B,D刚度矩阵ABHD_inverted A',B',D'柔度矩阵"""self.A = np.zeros([3,3], dtype=float)self.B = np.zeros([3,3], dtype=float)self.D = np.zeros([3,3], dtype=float)self.ply_prop ={}for plyid in range(1,total_ply_num + 1):ply = Get_lamina_prop(plyid)#将计算后的偏轴刚度、应变转换矩阵储存起来self.ply_prop['Q_'+str(plyid)] = ply.Qself.ply_prop['T_strain_' +str(plyid)] = ply.T_strainself.ply_prop['T_stress_'+str(plyid)] = ply.T_stresszk = z_coord_dict['z' + str(plyid)]zk_1 = z_coord_dict['z' + str(plyid-1)]for i in range(3):for j in range(3):self.A[i][j] += ply.Q_offaxis[i][j]*(zk - zk_1 )self.B[i][j] +=1/2.*ply.Q_offaxis[i][j]*(zk**2 - zk_1**2)self.D[i][j] +=1/3.*ply.Q_offaxis[i][j]*(zk**3 - zk_1**3)part1 = np.concatenate([self.A, self.B], axis=1)part2 = np.concatenate([self.B, self.D], axis=1)self.ABD = np.concatenate([part1, part2], axis=0)def calc_ABHD_inverted(self):# 计算ABD'柔度矩阵self.ABHD_inverted = lg.inv(self.ABD)def calc_equivalent_modulus(self):"""用于计算层合板等效的工程弹性常数:return:equiv_e1 等效E1equiv_e2 等效E2equiv_nu21 等效nu21equiv_nu12 等效nu12equiv_g12 等效G12"""AI = lg.inv(self.ABD)a11, a12, a22, a33 = AI[0,0], AI[0,1], AI[1,1], AI[2,2]self.equiv_e1 = 1./(z_total*a11)self.equiv_e2 = 1./(z_total*a22)self.equiv_nu21 = - a12 / a11self.equiv_nu12 = - a12 / a22self.equiv_g12 = 1./(z_total*a33)层合板强度预测
待更新。
最后的最后
欢迎大家点赞、评论及转载,转载请注明出处!
如果觉得我帮助到了你:
为我打call,不如为我打款!