spss系列——一元线性回归的分析与预测实例
- 散点图
- 回归系数
- 线性回归模型
- 区间估计
- 系数显著性检验
- 残差散点图
- 预测
- 感谢小伙伴们的浏览~~下期见喽
本文主要利用某商店记录了12个月的销售收入 y y y(亿元)和广告费 x x x(亿元),研究某广告对销售收入的影响,其数据见下表所示。
- 销售收人与广告费统计表
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x x x | 2 | 2 | 3 | 4 | 5 | 4.5 | 5.5 | 7.5 | 8 | 9 | 10 | 11 |
| y y y | 30 | 35 | 40 | 45 | 50 | 55 | 66 | 75 | 85 | 100 | 110 | 120 |
- 本期重点放在介绍一元线性回归在spss的运用以及对结果的分析,具体操作步骤我都详细列出来啦~~不会的朋友可以跟着操作,这里我就不放操作界面截图啦!
散点图
- Step1:将数据导进SPSS
- step2:点击“图形”——“旧对话框”——“散点图”——“简单散点图”画出散点图
- Step3:双击散点图激活——点击“元素”——“总计拟合线”作出拟合线
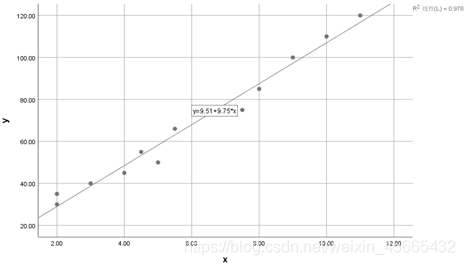
由散点图中的拟合线可以明显看出 x x x与 y y y大致呈线性关系,可以考虑做线性回归预测。
回归系数
用最小二乘法估计回归系数 β 0 {\beta_0} β0 和 β 1 {\beta_1} β1 的值
- Step1:点击“分析”——“回归”——“二阶最小平方”
- Step2:将 y y y 作为“因变量”, x x x 作为“解释变量”,月份为“工具变量”分析

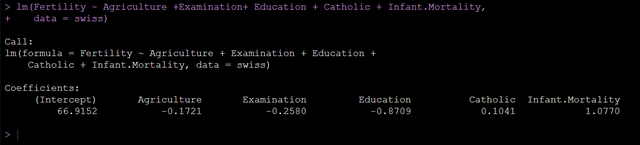
如图显示, β 0 ^ \hat{\beta_0} β0^=9.086, β 1 ^ \hat{\beta_1} β1^=9.818,所以可以得出回归模型为
y ^ = 9.086 + 9.818 x \hat{y}=9.086+9.818x y^=9.086+9.818x
线性回归模型
- Step1:点击“分析”——“回归”——“线性”
- Step2:将 y y y 作为“因变量”, x x x 作为“自变量”——点击“统计”——勾选
“回归系数”的“置信区间”——“级别”设定为95%
 由模型摘要可以看出回归标准差(级标准估算的错误) σ ^ \hat{\sigma} σ^=4.70420,决定系数( R R R 方)为0.978,即认为模型拟合很好,解释变量有97.8%的解释能力。
由模型摘要可以看出回归标准差(级标准估算的错误) σ ^ \hat{\sigma} σ^=4.70420,决定系数( R R R 方)为0.978,即认为模型拟合很好,解释变量有97.8%的解释能力。

从方差分析表ANOVA中看到, F F F=449.610,显著性近似为0,说明 y y y 对 x x x 的线性回归高度显著,模型具有统计意义。
区间估计

由图可以看出,
β 0 ^ \hat{\beta_0} β0^置信水平为95%的区间估计为(2.696,16.319),
β 1 ^ \hat{\beta_1} β1^置信水平为95%的区间估计为(8.723,10.771)。
系数显著性检验
由系数图可以看出回归系数 β 1 ^ \hat{\beta_1} β1^检验的 t t t 的值为21.204,显著性近似为0,则认为对回归系数 β 1 ^ \hat{\beta_1} β1^ 的估计高度显著。
- 可注意到与前面直接做最小二乘法的结果有细微差异,这是由于方法使用时的置信度略有不同,计算方式和结果不同,但不影响结果,估计值两种皆可用。
残差散点图
Step1:计算残差值保存为“*ZPRED ”,预测值保存为“*ZRESID”
Step2:点击“分析”——“回归”——“线性”
Step3:点击“图”——将“*ZPRED ”作为Y,将“ *ZRESID”作为X,画出标准化残差的散点图
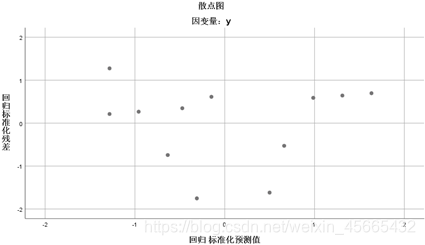
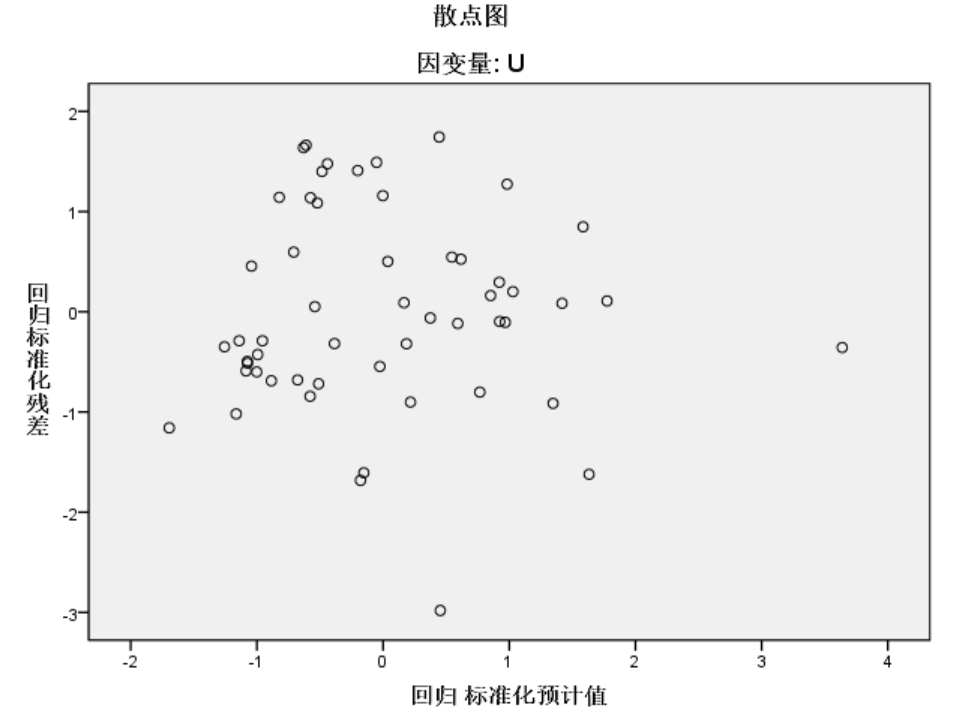
如残差散点图所示,回归标准化残差在区间(-2.2)内波动,则说明拟合程度好。
预测
当广告费用为4.2亿元时,销售收入将达到多少?并给出置信水平95%的置信区间。
Step1:在 x x x 那一列后面添加一个4.2的值
Step2:点击“分析”——“回归”——“线性”
Step3:将 y y y 作为“因变量”, x x x 作为“自变量”——点击“统计”——勾选“回归系数”的“估算值”得出一列预测值。
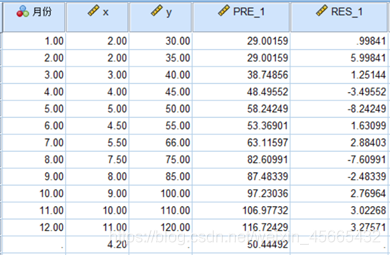
由图可得出当广告费用( x x x )为4.2亿元时,销售收入( y y y )的预测值为50.44492.

上图显示,残差的标准偏差为4.48527,则置信水平95%的置信区间为50.44492 4.48527,即为(45.95965,54.93019)
感谢小伙伴们的浏览~~下期见喽
跟着这个实例,简单线性回归模型的spss基本操作和使用就完成啦,还有不懂得或补充的问题欢迎留言哦~~