1 层次分析法的原理及步骤
1.1 层次分析法的原理
20世纪70年代末,美国运筹学家、匹兹堡大学教授T.L.萨迪(T.L.Saaty)提出了层次分析法(Analysis Hierarchy Process,简称 AHP)。它将人的思维过程分成目标层、准则层和方案层,并借助数学模型进行分析,是一种将决策者定性判断和定量计算有效结合起来的实用的决策分析方法。该方法系统性强,使用灵活、简便,适用于组织化的大规模复杂系统。尤其是当系统规模庞大、结构复杂、属性及目标多样,且系统中很多要素指标仅有定性关系时,采用层次分析法进行评价和决策是非常高效的。层次分析法的基本原理是把复杂问题按支配关系分成递阶层次结构,每个层次都有相互联系相互作用的各个要素组成。通过逐对比较法对层次中各要素的相对重要性进行量化,最后进行相对重要性的总排序。
1.2 层次分析法的应用步骤
运用AHP法进行决策时,需要经历以下4个步骤:
1.2.1 建立多级递阶的结构模型
按支配关系自上而下分三层建立评价指标体系:
(1)最高层:也称目的层或目标层,是系统想要达到的目标或结果,是系统评价的首要准则(如评价高校教师教学质量)。
(2)准则层:是为实现目标层所设立的准则、子准则等。
(3)最底层:也称方案层。是为实现目标所采取的各种方案、措施等。
1.2.2 构造两两比较判断矩阵
对同属一级的要素,以上一级的要素为准则进行逐对比较,建立判断矩阵。
比较n个要素B=(B1,B2,Bn)对目标层要素A的影响:采用两两成对比较,用aij表示要素Bi与要素Bj对目标A的影响程度之比。
为了使判断定量化,根据1-9标度确定每个要素的相对重要度。

1.2.3 权重计算
(1)用求根法来计算判断矩阵特征向量的近似值。

(2)把特征向量标准化后得到权重向量W=(W1,W2,…,Wn)T。
1.2.4 一致性检验
为保证求得的权重的正确性及合理性,还需要进行一致性检验。
计算一致性指标C.I.

其中,
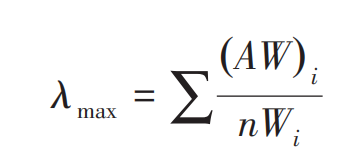
显然,n越大,C.I.的误差越大。因此,在检验时引入随机性一致性比值C.R.
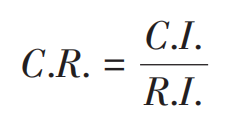
当n=1,2,…,15时,R.I.的取值见下表。
![]()
当随机一致性比率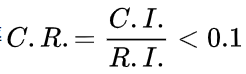
时认为计算所得的层次排序权重是正确的、合理的,否则,需要重新调整判断矩阵,直到一致性检验合格为止。
1.2.5 综合重要度的计算
权重最大的方案即为实现目标的最优选择。
2 高校教师教学质量评价指标体系
高校教师教学质量评价的目的是对被评价的对象作出有价值的判断,以便促进教学。做好教学质量评价的首要问题是建立科学的评价指标体系。该评价指标体系应能准确、灵敏地反映教师当前的教学水平。
根据高校教师教学质量评价指标体系特点和可操作性,设定了四个准则层和三个方案对象。
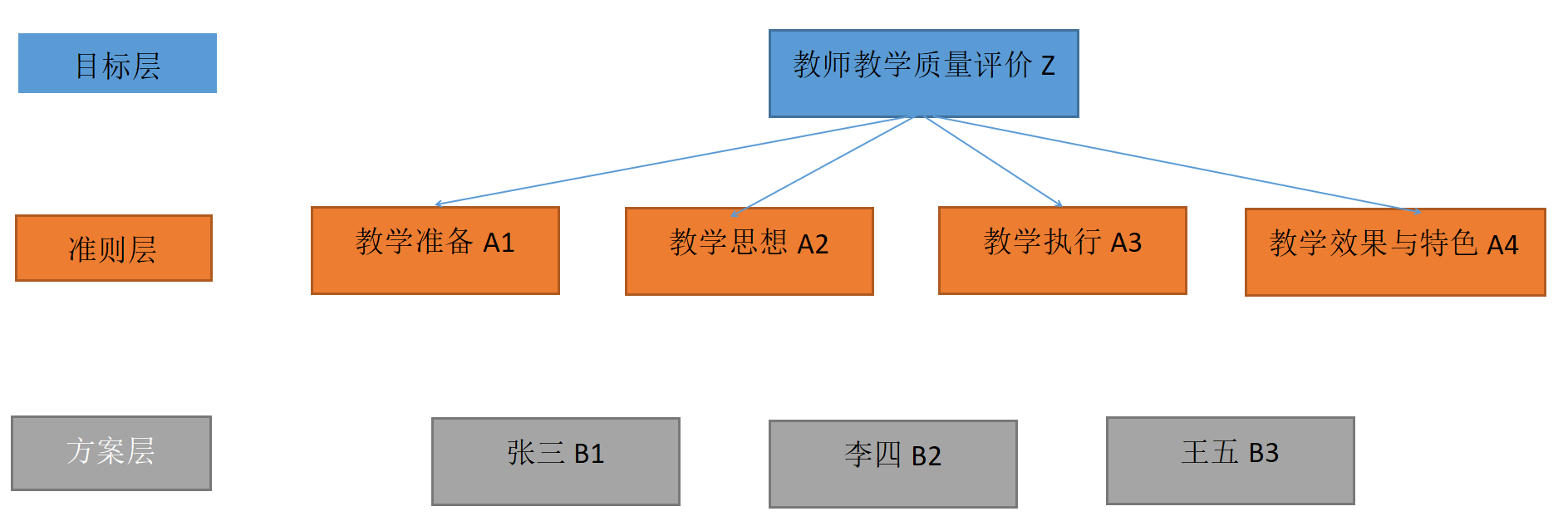
对于准则层:教学准备,教学思想,教学执行,教学效果与特色,我们可以构建这样一个4*4的判断矩阵:

其中对角线为各个指标自己的判断,例如对于【教学准备】与【教学准备】,其重要性为1,因为肯定是指标自身对比自身肯定是1:1。对于第二行第一列,也就是【教学思想】与【教学准备】对比,可能我认为【教学准备】比【教学思想】明显重要,那么就可以标值为0.7,以此类推,直到构建一个完整的判断矩阵。
标准化后权重W为:

其中A*W为:

AW:

λmax=AW1/W1+AW2/W2+AW3/W3+···+AWn/Wn=x

最大特征值λmax=x/矩阵阶数=4.0489
最大特征值λmax求解出来后,C.I值就好算多了,
根据C.I值公式,λmax=4.0489,n=4,代入可得C.I值=0.0163
![]()
根据CI、RI值求解CR值,判断其一致性是否通过。
RI值通过查表可以得知,这个是Satty 模拟 1000 次得到的随机一致性指标 R.I.取值表(如下表所示):

而我们的矩阵是4阶(准则层因子个数),矩阵阶数为4时对应的RI值为0.90,代入公式:
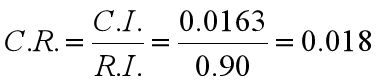
所以 C.R.=0.018<0.1 时,表明判断矩阵 A 的一致性程度被认为在容许的范围内,此时可用A的特征向量开展权向量计算;若 C.R.≥0.1, 说明我们在构建判断矩阵时出现了逻辑错误。
对于方案层:张三,李四,王五,我们可以构建这样一个3*3的判断矩阵:

通过层次单排序两两对比各个方案在教学准备的比较,我们可以得到张三,李四,王五的权重,那么这个权重就可以作为张三,李四,王五在教学准备上的得分。
依次类推,我们构造得到张三,李四,王五在教学准备、教学思想、教学执行、教学效果与特色上的得分矩阵:



计算得到其得分为:
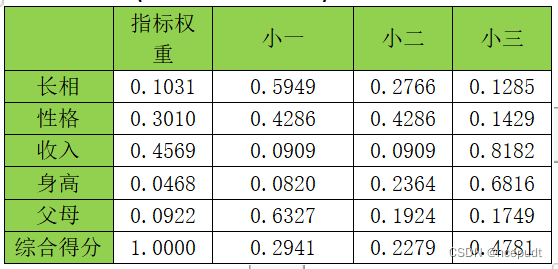
张三,李四,王五对教学准备的权重为【0.5954,0.2764,0.1283】
张三,李四,王五对教学思想的权重为【0.0819,0.2363,0.6817】
张三,李四,王五教学执行的权重为【0.6337,0.1919,0.1744】
张三,李四,王五对教学效果与特色的权重为【0.1667,0.1667,0.6667】
PS:以上全部的判断矩阵都需要做一致性检验。
那么对于方案对象B1(张三),它的总得分为:
张三在教学准备上的得分*教学准备的权重+张三在教学思想上的得分*教学思想的权重+张三在教学执行上的得分*教学执行的权重+张三在教学效果与特色上的得分*教学效果与特色的权重=0.5954*0.2082+0.819*0.199+0.6337*0.4247+0.1667*0.1681=0.5841
以此类推,可以计算得到方案对象B2(李四)为:
0.2764*0.2082+0.2363*0.199+0.1919*0.4247+0.1667*0.1681=0.2141
方案对象B3(王五):
0.1283*0.2082+0.6817*0.199+0.1744*0.4247+0.6667*0.1681=0.3485
因此张三得分最高,其次是王五,最后是李四。
3、案例以及工具实现
3.1 评价教学质量最重视的因素
这里的作用其实就是求因子权重,因此只计算到层次单排序,没有方案层,即无需层次总排序。
3.1.1 使用工具
SPSSPRO(免费在线,所有功能全部免费)—>【层次分析法(AHP简化版)】
3.1.2 案例操作
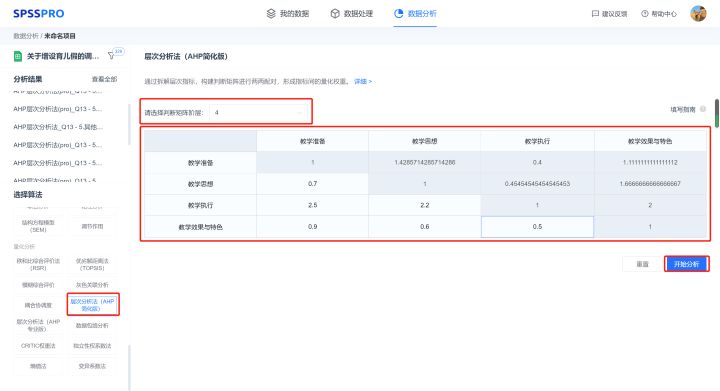
step1:选择【层次分析法(AHP简化版)】;
step2:选择判断矩阵阶层
step3:设置判断矩阵(判断矩阵是对称矩阵)
step4:点击【开始分析】,完成全部操作。
3.1.3 分析结果解读
以下生成的结果来源于SPSSPRO软件的分析结果导出
输出结果1:构建判断矩阵结果

这个就是前面操作页面所填写的判断矩阵
输出结果2:AHP层次分析结果

层次分析法(方根法)的权重计算结果显示,教学准备的权重得分为0.2082,教学思想的权重得分为0.199,教学执行的权重得分为0.4247,教学效果与特色的权重得分为0.1681。
输出结果3:一致性检验结果

层次分析法的计算结果显示,最大特征根为4.0814,根据RI表查到对应的RI值为0.882,因此CR=CI/RI=0.0308<0.1,通过一次性检验,说明该权重确定方法的合理性,无需要对判断矩阵进行修改。
3.1.4 小结
由3.1.3可知,评价教学质量最重要的因素是教学执行,其权重得分为0.4247,其次是教学准备,教学思想,最后是教学效果与特色。
3.2 选择最佳教师
这里的作用其实就是求方案的量化得分,因此需要对准则层计算层次单排序,对方案层进行层次总排序。
3.2.1 使用工具
SPSSPRO(免费在线,所有功能全部免费)—>【层次分析法(AHP专业版)】
3.2.2 案例操作
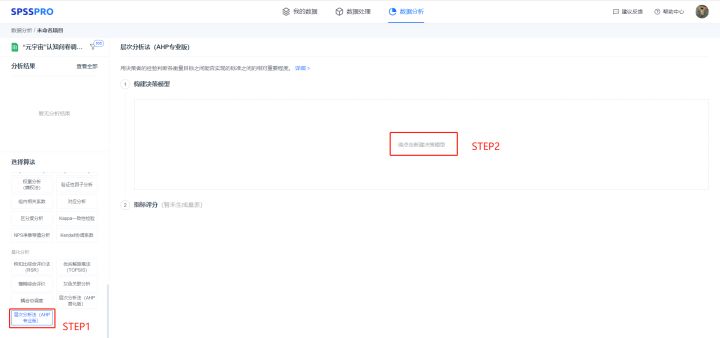
Step1:选择层次分析法(AHP专业版);
Step2:选择构建决策模型;
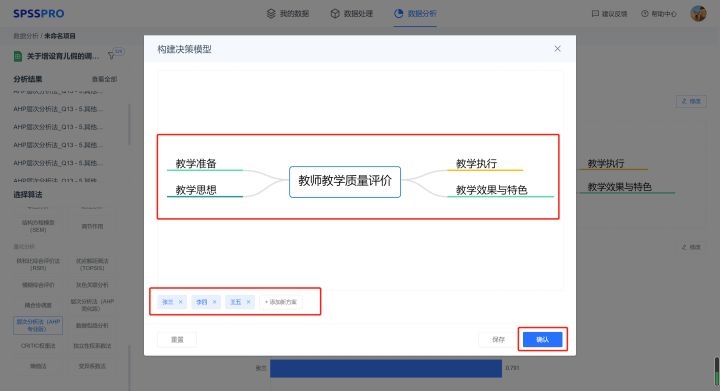
Step3:输入构建的评价指标;
Step4:输入最终的方案;
Step5:确认以进入下一步指标评分(只接受整数);
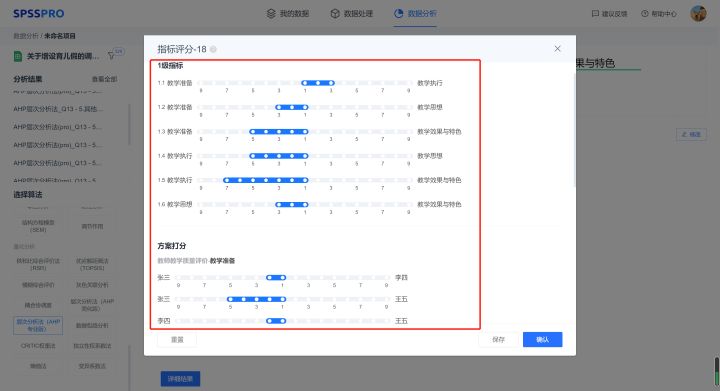
Step6:输入指标之间两两比对的重要程度值;
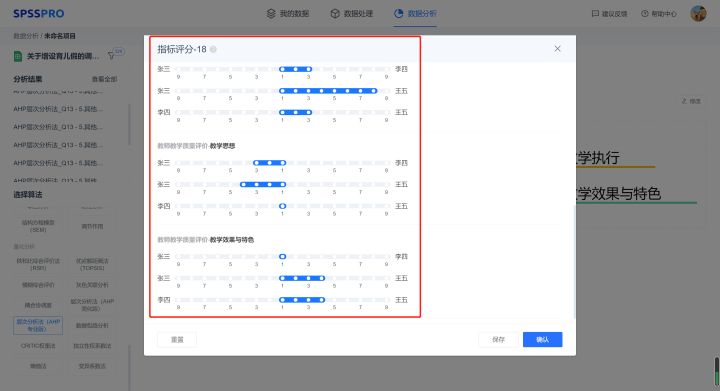
Step7:输入不同方案的对应评价值的重要程度评价;
3.1.3 分析结果解读
以下生成的结果来源于SPSSPRO软件的分析结果导出
输出结果1:方案得分
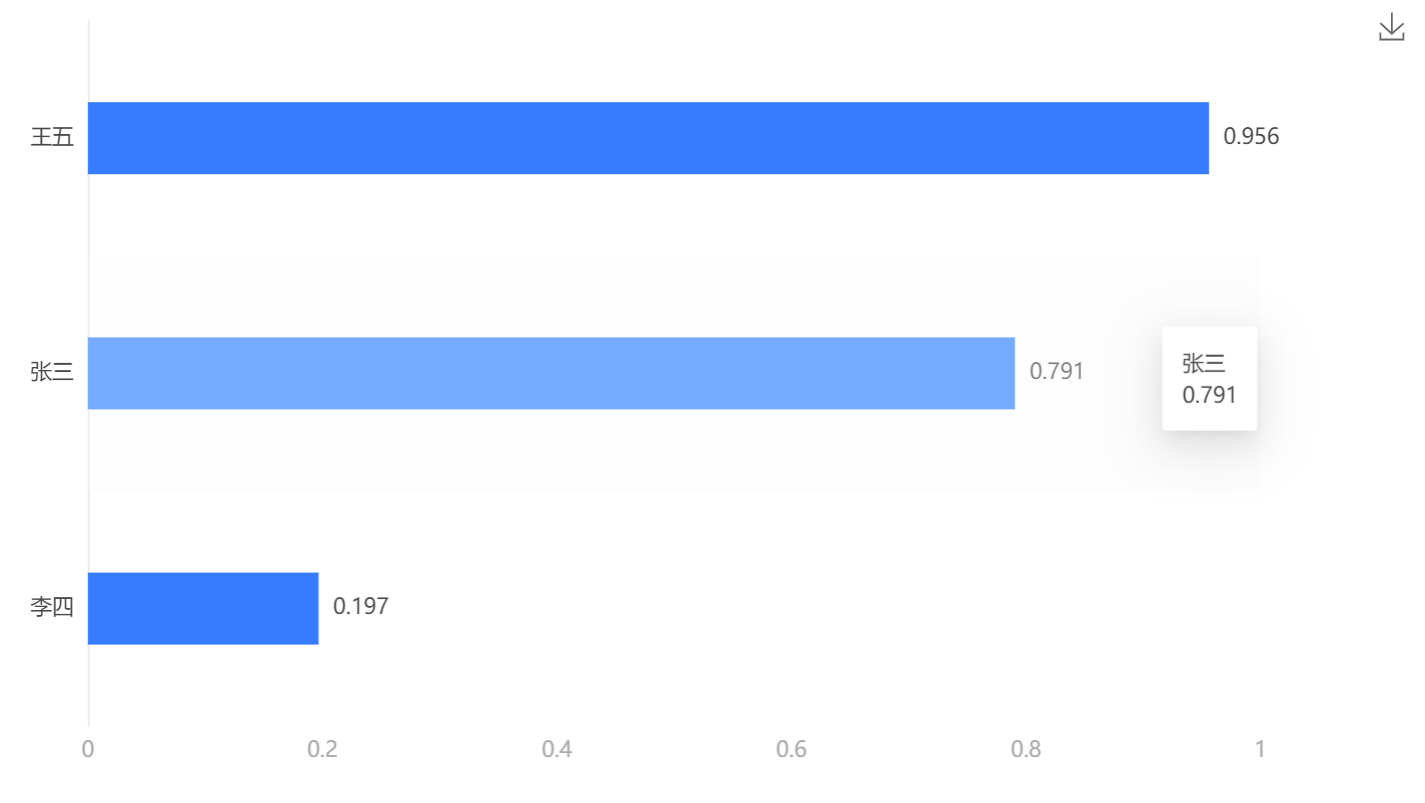
基于指标层次单排序与方案层次总排序后,对于教师教学质量评价最好的方案为王五,其量化得分为0.9561。
输出结果2:层次决策模型

由图可见,其中最重要的两个决定因素是教学执行和教学准备,而教学思想、教学效果与特色情况则属于低权重。
输出结果3:判断矩阵汇总结果

该判断矩阵最大特征值为4.117,CI值为0.039,RI值为0.882,CR值为0.0442,一致性验证通过。
输出结果4:方案层判断矩阵汇总结果

上表展示了层次分析法的方案层的权重计算结果(即层次总排序),构建了个数为叶子节点指标的数目的判断矩阵对各个指标的权重进行分析,通过展示了一致性检验结果,用于判断方案层权重矩阵是否存在构建判断矩阵的逻辑问题。
由于上一级节点的得分可以根据其子节点得分*权重计算得到,因此构建方案层判断矩阵时,只对叶子节点进行构建,即N个叶子节点就构建N个判断矩阵,用于综合两两对比情况,得到方案层对于某个叶子节点的得分;
一致性检验结果要求CR值(CR=CI/RI)小于0.1,可以看到,方案的得分都满足了一致性检验。
3.2.4 小结
由3.2.3可以知道,对于教师教学质量评价分数最高的教师为王五,其量化得分为0.956
4 结论
利用层次分析法进行教学评估可较大幅度地减少主观因素。一方面,在层次分析法中构造判断矩阵时,比起确定的数值,它需要的是影响因素两两比较的相对比值,这就大大减少了评价专家的主观随意性;另一方面,在评判专家的主观判断是否偏离客观实际时,运用了检验判断矩阵一致性来在分析评价,从而得以做出正确的调整。 然而,层次分析法也存在着一些问题,比如影响因素权值计算不准确。这是由于判断矩阵在传统的层次分析法中并非都能够满足一致性要求。本文针对该问题,在传统的层次分析法基础上提出了人机结合的新方法,在判断矩阵一致性时提高了其准确性和效率,保障了权值计算的准确性,有效地改进传统的层次分析法。