Python微信订餐小程序课程视频

https://edu.csdn.net/course/detail/36074

Python实战量化交易理财系统

https://edu.csdn.net/course/detail/35475
本文将介绍密码学中的PRF、PRP等相关概念，并介绍 PRP/PRF 转换引理及其证明，希望读完本文后，你能对现代密码学中这几个基础概念有所了解。

在开始本文前，希望你有如下预备知识：

• 现代密码学是怎样的一门学科？
• “Security Through Obscurity” 是什么意思？
• 集合、极限、函数、随机变量、采样等数学概念是什么？

概述

在之前的一篇博客中提到，伪随机性是现代密码学的根基，每一个密码算法都需要有这样的伪随机性来源。而伪随机数发生器只是一个承载伪随机性的初等原语，其数学性质和模型都太朴素，不足以帮助我们构建更复杂的算法结构。

而伪随机函数的出现，对「如何将随机性这个特点与函数的输入输出结合？」这一问题给出了严格的数学定义与描述方法。这为各位密码学家们提供了一个很强的模型。进一步地，伪随机置换则在此基础上，引入了「映射可逆」的概念，从而丰富和细化了PRF的抽象能力。

这篇博客将依次介绍伪随机数发生器（PRNG）、伪随机函数（PRF）、伪随机置换（PRP），并给出大名鼎鼎的 PRF/PRP 转换引理及其证明。

PRNG

伪随机性之于现代密码学的重要性在之前的博客中已经为大家介绍过了，而作为伪随机性的载体，伪随机数发生器（Pseudorandom Number Generator，PRNG）的定义重新陈述如下：

令GGG为一多项式时间算法，其输入为s∈{0,1}ns∈{0,1}ns\in {0, 1}^{n}，即为一长度为nnn的01比特串，输出的长度记作l(n)l(n)l(n)。其中，l(⋅)l(⋅)l(\cdot )也为一多项式时间算法，l(n)l(n)l(n)则表示是nnn的多项式界（如 n2n2n^{2}、nnn）下的一个数值。若GGG为一PRNG，则应同时满足如下两个条件：

• 对于任意的nnn，都有l(n)>nl(n)>nl(n) > n；
• 若此时对于任意一具有多项式资源的敌手AA\mathcal{A}，都存在一个可忽略（negligible）的概率 ϵϵ\epsilon ，使得下式成立：

|Pr[A®=1]−Pr[A(G(s))=1]|≤ϵ(1)(1)|Pr[A®=1]−Pr[A(G(s))=1]|≤ϵ|\mathrm{Pr}[\mathcal{A}®=1] - \mathrm{Pr}[\mathcal{A}(G(s))=1]| \le \epsilon \tag{1}
PRNG作为伪随机性最直观的抽象模型，示意图如下图所示。

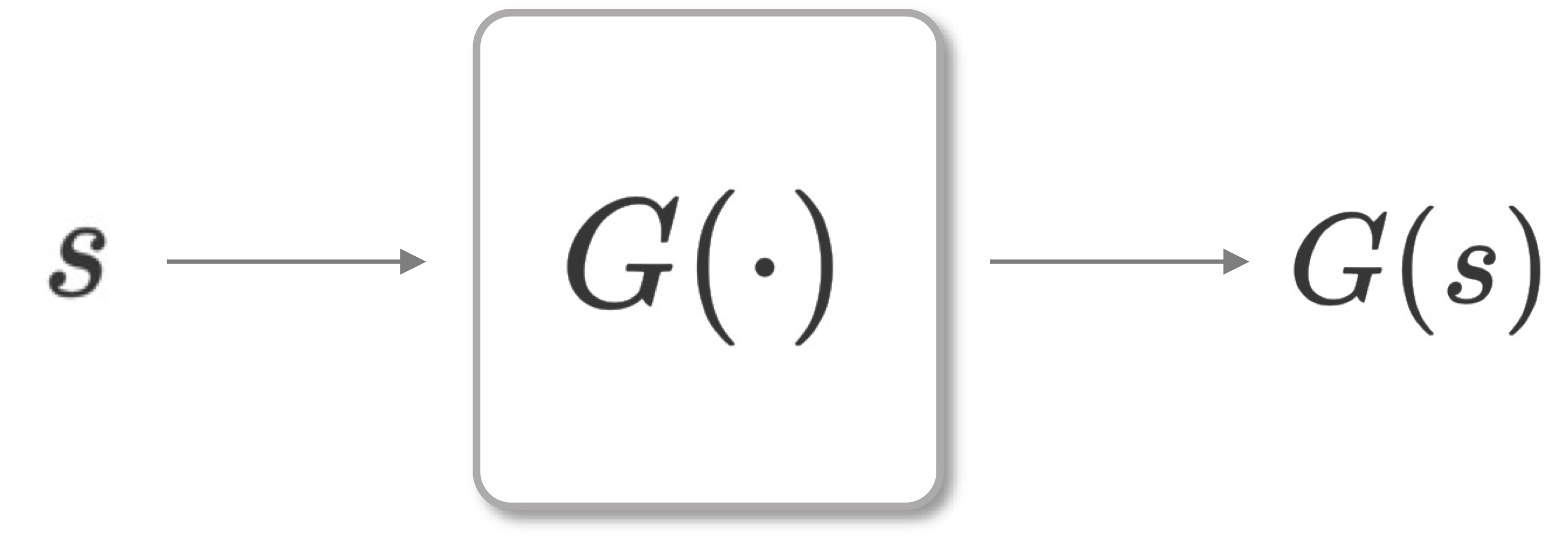
可以看到，PRNG在算法构建上的表现力似乎还不是很强。例如，G(s)G(s)G(s)作为PRNG的输出，但这和一个密码算法到底有啥关系？生成密钥？可一个算法又不只有密钥，还有输入输出呢！因此，PRNG作为一个初等原语，其抽象能力还是有些弱，这就需要表达能力更强的原语了。

PRF与PRP

PRF

伪随机函数（即 Pseudorandom Function, PRF）与PRNG相比，多了对输入输出的描述，而这正是「函数」的意义。在介绍PRF之前，首先介绍随机函数。

随机函数

对于将nnn位比特串{0,1}n{0,1}n{0, 1 }^{n}映射到nnn位比特串{0,1}n{0,1}n{0, 1 }^{n}的所有函数组成的函数族FF\mathcal{F}，一个随机函数fff是指在FF\mathcal{F}中以均匀随机采样的方法选择得到的一个函数，即有f∈rndFf∈rndFf \stackrel{rnd} \in \mathcal{F}.

在该函数族中，一个函数相当于给出了一种2n2n2^{{n}个nnn比特长的串的排列，那么整个函数族的大小即为2n⋅2n2n⋅2n2}{n\cdot 2^{n}}。这是一个指数级别的计算规模，因此即使存在一个多项式资源的敌手或区分器，他也无法在多项式时间内建模某个随机函数fff的映射方式。

伪随机函数

PRF的正式定义如下：

对于一类带密钥的函数FFF，有F:{0,1}∗×{0,1}∗→{0,1}∗F:{0,1}∗×{0,1}∗→{0,1}∗F: {0,1}^{} \times {0, 1}^{} \rightarrow {0, 1}^{*}，即y←F(k,x)y←F(k,x)y \leftarrow F(k, x)，其中xxx为输入，kkk为密钥，yyy为输出。若称FFF为PRF，则可满足以下条件：

• 高效计算：给定kkk与xxx，存在高效的多项式时间算法能计算y=F(k,x)y=F(k,x)y=F(k, x)；
• 不可区分：随机选定密钥kkk，伪随机函数F(k,⋅)F(k,⋅)F(k, \cdot)与一随机函数f(⋅)f(⋅)f(\cdot)是不可区分的；
• 长度保留：y、x、ky、x、ky、x、k的长度均为nnn；该性质是非必需的。

可以看到，PRF的性质和很多密码算法都有共性了：接收一个输入，返回一个看起来是随机输出的函数，而这种伪随机性来自于密钥，只要密钥kkk不被敌手获取，F(k,x)F(k,x)F(k, x)的映射性质就无法被建模或攻破。因此，在有些地方，PRF会被定义成「在函数族F中F中\mathcal{F}中，由密钥kkk作为索引的随机函数」，记作Fk(⋅)Fk(⋅)F_{k}(\cdot)。

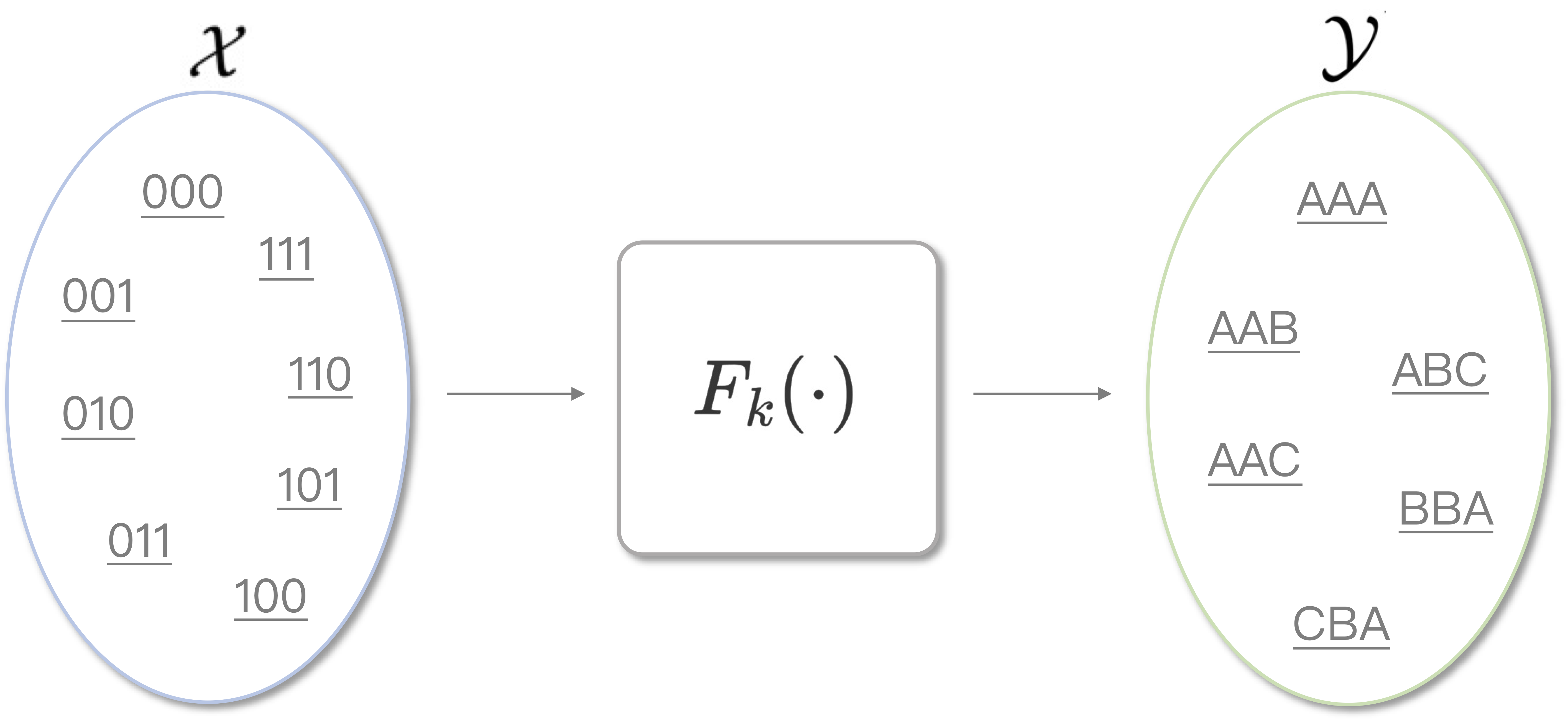
综上，两种PRF定义都可以用上面的示意图来表示。而不论哪种定义，PRF都会涉及密钥、输入、输出三个要素，这正好可以与常见的密码算法是相同的，消息认证算法就是一种PRF，对称加密算法在广义上也是一种PRF。在PRF的模型下，我们似乎可以刻画出更多的安全性质，例如输出的不可区分性，输出的单向性等等。PRF丰富了伪随机性的范围和尺度，让其能更好地贴合人们的直觉。

尽管PRF能帮助我们抽象不同的密码算法，但是却不能很好地刻画输入与输出之间的映射关系。没错，借助PRF的确能构建出xxx到yyy的映射关系，但对加解密算法而言，xxx与yyy之间需要是严格的双射。因此，为进一步加强PRF对这类「可逆」密码算法的表现能力，一种新的原语出现了。

PRP

伪随机置换（即 Pseudorandom Permutation，PRP）与PRF相比，多了对xxx到yyy映射关系可逆的要求，而这也是「置换」的意义。同样地，此处将先介绍随机置换。

随机置换

对于将nnn位比特串{0,1}n{0,1}n{0, 1 }^{n}映射到自身的所有置换组成的置换族PP\mathcal{P}，一个随机置换ppp是指在PP\mathcal{P}中以均匀随机采样的方法选择得到的一个置换，即有p∈rndPp∈rndPp \stackrel{rnd} \in \mathcal{P}.

同理，由于置换一定是双射的，因此该置换族的大小等价于所有输出的全排列数量，即为(2n)!(2n)!(2^{n})!；但这同样是一个远大于多项式（super poly）级别的计算规模，因此即使存在一个多项式资源的敌手或区分器，他也无法在猜出或建模出某个随机置换ppp的映射方式。

伪随机置换

PRP的正式定义如下：

对于一类带密钥的置换PPP，有P:{0,1}∗×{0,1}n→{0,1}nP:{0,1}∗×{0,1}n→{0,1}nP: {0,1}^{*} \times {0, 1}^{n} \rightarrow {0, 1}^{n}，即y←P(k,x)y←P(k,x)y \leftarrow P(k, x)，其中xxx为输入，kkk为密钥，yyy为xxx对应的置换后结果。若称PPP为PRP，则可满足以下条件：

• 高效计算：给定kkk与xxx，存在高效的多项式时间算法能计算y=P(k,x)y=P(k,x)y=P(k, x)；给定kkk与yyy，存在高效的多项式时间可逆算法能计算x=P−1(k,y)x=P−1(k,y)x=P^{-1}(k, y)
• 不可区分：随机选定密钥kkk，伪随机置换P(k,⋅)P(k,⋅)P(k, \cdot)与一随机置换p（⋅)p（⋅)p（\cdot)是不可区分的；
• 长度保留：y、xy、xy、x的长度均为nnn。

可以看到，与PRF相比，PRP的定义实质上就是将原来的「函数」变为「置换」，即xxx与yyy此时位于同一概率空间中，之间的映射关系为双射，示意图如下图所示。PRP对于那些具备逆运算的密码算法而言，能更好地描述输入和输出之间的可逆映射关系，因此更适合用于刻画加解密算法时。至此，现代密码学中三个非常重要的原语已经全部介绍完毕。

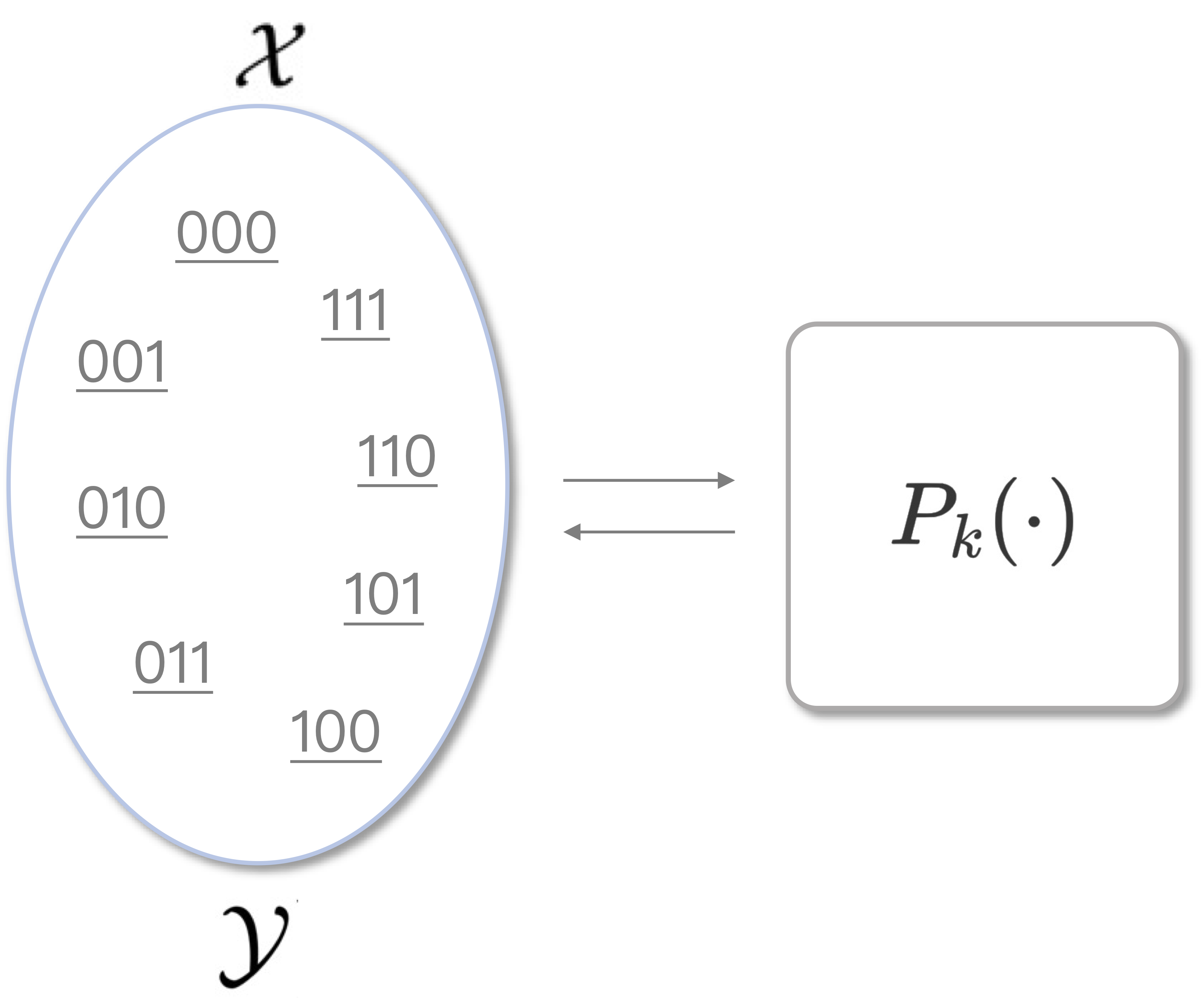
不可区分性

上文介绍PRF与PRP时，未阐述究竟是如何不可区分的，但这一性质实际上是密码学计算安全性的核心，本节将予以重点介绍。

PRF的不可区分性

一个长度保留的、可高效计算的PRF Fk(⋅)Fk(⋅)F_{k}(\cdot)的不可区分性表示为，对于任意的具有多项式规模资源的敌手AA\mathcal{A}，都存在一个可忽略的极小概率ϵ(n)ϵ(n)\epsilon(n)，使得下式成立：

|Pr[AFk(⋅)(1n)=1]−Pr[Af(⋅)(1n)=1]|≤ϵ(n)(2)(2)|Pr[AFk(⋅)(1n)=1]−Pr[Af(⋅)(1n)=1]|≤ϵ(n)|\mathrm{Pr}[\mathcal{A}^{{F_{k}(\cdot)}(1}{n})=1] - \mathrm{Pr}[\mathcal{A}^{f(\cdot)}(1{n})=1]| \le \epsilon(n) \tag{2}
其中ϵ(n)ϵ(n)\epsilon(n)是指与长度参数nnn相关的一个可忽略概率，例如12n12n\frac{1}{2^{{n}}；AFk(⋅)(1n)=1AFk(⋅)(1n)=1\mathcal{A}}{F_{k}(\cdot)}(1^{{n})=1以及Af(⋅)(1n)=1Af(⋅)(1n)=1\mathcal{A}}{f(\cdot)}(1^{{n})=1分别表示敌手AA\mathcal{A}在未知当前函数是Fk(⋅)Fk(⋅)F_{k}(\cdot)或f(⋅)f(⋅)f(\cdot)的条件下，正确猜出了这个函数是什么。1n1n1}{n}表示函数参数规模为nnn。因此，式(2)可以写作：

|Pr[A认为当前函数是伪随机函数|当前函数是伪随机函数]−Pr[A认为当前函数是随机函数|当前函数是随机函数]|≤ϵ|Pr[A认为当前函数是伪随机函数|当前函数是伪随机函数]−Pr[A认为当前函数是随机函数|当前函数是随机函数]|≤ϵ|\mathrm{Pr}[\mathcal{A} 认为当前函数是伪随机函数|当前函数是伪随机函数] \

• \mathrm{Pr}[\mathcal{A} 认为当前函数是随机函数|当前函数是随机函数]| \le \epsilon

实际上，敌手AA\mathcal{A}在辨别当前函数是谁的这种情景，在现代密码学的语义下，通常称敌手AA\mathcal{A}与一个寓言机（Oracle）OO\mathcal{O}进行询问（query）游戏（Game），OO\mathcal{O}的内部可能是Fk(⋅)Fk(⋅)F_{k}(\cdot)或f(⋅)f(⋅)f(\cdot)。而根据每次询问OO\mathcal{O}返回的输出，AA\mathcal{A}最终输出对OO\mathcal{O}的猜测结果。示意图如下所示。

如图所示，敌手AA\mathcal{A}在与OO\mathcal{O}询问若干次后，若能正确判定自己面前的这个OO\mathcal{O}的内部究竟是一个伪随机函数还是一个随机函数，那就称AA\mathcal{A}攻破了PRF的不可区分性。换言之：

• 当敌手能轻易区分何时是PRF，何时是随机函数时，说明敌手攻破PRF的优势足够大；
• 当敌手对这二者是不可区分时，说明敌手攻破PRF的优势很小。

因此，敌手的这种区分能力其实就是敌手攻破PRF的优势，那么式(2)还可以写作：

AdvPRFO(A)=|Pr[AFk(⋅)(1n)=1]−Pr[Af(⋅)(1n)=1]|≤ϵ(n)AdvOPRF(A)=|Pr[AFk(⋅)(1n)=1]−Pr[Af(⋅)(1n)=1]|≤ϵ(n)\mathrm{Adv}_{\mathcal{O}}^{{PRF}(\mathcal{A})=|\mathrm{Pr}[\mathcal{A}}{F_{k}(\cdot)}(1^{n})=1] - \mathrm{Pr}[\mathcal{A}^{f(\cdot)}(1{n})=1]| \le \epsilon(n)
其中，AdvPRFO(A)AdvOPRF(A)\mathrm{Adv}_{\mathcal{O}}^{PRF}(\mathcal{A})即为敌手AA\mathcal{A}面对寓言机OO\mathcal{O}时进行不可区分实验的优势。

PRP的不可区分性

一个长度保留的、可高效计算的PRP Pk(⋅)Pk(⋅)P_{k}(\cdot)的不可区分性表示为，对于任意的具有多项式规模资源的敌手 AA\mathcal{A}，都存在一个可忽略的极小概率 ϵ(n)ϵ(n)\epsilon(n)，使得下式成立：

|Pr[APk(⋅)(1n)=1]−Pr[Ap(⋅)(1n)=1]|≤ϵ(n)(3)(3)|Pr[APk(⋅)(1n)=1]−Pr[Ap(⋅)(1n)=1]|≤ϵ(n)|\mathrm{Pr}[\mathcal{A}^{{P_{k}(\cdot)}(1}{n})=1] - \mathrm{Pr}[\mathcal{A}^{p(\cdot)}(1{n})=1]| \le \epsilon(n) \tag{3}
同理，APk(⋅)(1n)=1APk(⋅)(1n)=1\mathcal{A}^{{P_{k}(\cdot)}(1}{n})=1以及Ap(⋅)(1n)=1Ap(⋅)(1n)=1\mathcal{A}^{p(\cdot)}(1{n})=1分别表示敌手AA\mathcal{A}在当前的寓言机OO\mathcal{O}的确是Pk(⋅)Pk(⋅)P_{k}(\cdot)或p(⋅)p(⋅)p(\cdot)的条件下，正确猜出了这个置换是什么。示意图如下图所示。

在PRP不可区分实验中，引入敌手的优势改写式(3)如下：

AdvPRPO(A)=|Pr[APk(⋅)(1n)=1]−Pr[Ap(⋅)(1n)=1]|≤ϵ(n)AdvOPRP(A)=|Pr[APk(⋅)(1n)=1]−Pr[Ap(⋅)(1n)=1]|≤ϵ(n)\mathrm{Adv}_{\mathcal{O}}^{{PRP}(\mathcal{A})=|\mathrm{Pr}[\mathcal{A}}{P_{k}(\cdot)}(1^{n})=1] - \mathrm{Pr}[\mathcal{A}^{p(\cdot)}(1{n})=1]| \le \epsilon(n)

PRP/PRF转换引理与证明

这个引理能做什么？

一个安全的加解密算法E=(E,D)E=(E,D)\mathcal{E}=(E, D)可以抽象成一个实现了PRP的寓言机。由于在对称算法的设计中，EEE与DDD的算法结构通常是对合的（Involution）。因此在证明EE\mathcal{E}的安全性时，只考虑加密算法EEE即可。这时，如果EEE是安全的，则既可被证明是一个PRP寓言机，也可被证明是一个PRF寓言机。证明EEE的安全性，也就是回答下面两个问题之一：

• 能否证明EEE是一个PRP（即AdvPRPE(A)AdvEPRP(A)\mathrm{Adv}_{E}^{PRP}(\mathcal{A})是否为可忽略的？）
• 能否证明EEE是一个PRF（即AdvPRFE(A)AdvEPRF(A)\mathrm{Adv}_{E}^{PRF}(\mathcal{A})是否为可忽略的？）

而许多时候，PRP所代表的这种「置换」模型的安全性并不利于证明工作的推进，如果将其归约到PRF这种更符合一般数学直觉的「函数」模型上，概率空间的定义、碰撞事件等问题都可以在函数的框架下进行计算和讨论，这为证明的抽象和表示带来了方便。

因此，在加解密算法尤其是分组密码的安全性证明中，该引理能将证明工作的重心转换到更为熟悉和直观的「函数」模型上。

PRP/PRF转换引理

铺垫了这么多，终于该介绍这个转换引理的内容了。

令AA\mathcal{A}为一具有多项式资源的敌手，AA\mathcal{A}对寓言机OO\mathcal{O}最多能进行qqq次询问，OO\mathcal{O}内部可能实现了一个随机函数fff，也可能实现了一个随机置换ppp。对于整数n≥1n≥1n \ge 1，则下式[1]成立：

|Pr[Af(⋅)(1n)=1]−Pr[Ap(⋅)(1n)=1]|≤q(q−1)2n+1(4)(4)|Pr[Af(⋅)(1n)=1]−Pr[Ap(⋅)(1n)=1]|≤q(q−1)2n+1|\mathrm{Pr}[\mathcal{A}^{f(\cdot)}(1{n})=1] - \mathrm{Pr}[\mathcal{A}^{p(\cdot)}(1{n})=1]| \le \frac{q(q - 1)}{2^{n+1}} \tag{4}
通常，我们认为敌手不会发送两次相同的询问。若考虑到敌手优势的定义，则有：

|AdvPRPE(A)−AdvPRFE(A)|=∣∣|Pr[AE(k,⋅)(1n)=1]−Pr[Af(⋅)(1n)=1]|−|Pr[AE(k,⋅)(1n)=1]−Pr[Ap(⋅)(1n)=1]|∣∣≤|Pr[Af(⋅)(1n)=1]−Pr[Ap(⋅)(1n)=1]||AdvEPRP(A)−AdvEPRF(A)|=||Pr[AE(k,⋅)(1n)=1]−Pr[Af(⋅)(1n)=1]|−|Pr[AE(k,⋅)(1n)=1]−Pr[Ap(⋅)(1n)=1]||≤|Pr[Af(⋅)(1n)=1]−Pr[Ap(⋅)(1n)=1]|\begin{align*}
|\mathrm{Adv}_{E}^{PRP}(\mathcal{A})- \mathrm{Adv}_{E}^{PRF}(\mathcal{A})|
&= \left| |\mathrm{Pr}[\mathcal{A}^{{E(k,\cdot)}(1}{n})=1] - \mathrm{Pr}[\mathcal{A}^{f(\cdot)}(1{n})=1]|-|\mathrm{Pr}[\mathcal{A}^{E(k, \cdot)}(1^{n})=1] - \mathrm{Pr}[\mathcal{A}^{p(\cdot)}(1{n})=1]|\right| \
&\le |\mathrm{Pr}[\mathcal{A}^{f(\cdot)}(1{n})=1] - \mathrm{Pr}[\mathcal{A}^{p(\cdot)}(1{n})=1]| \
\end{align*}
因此该引理还有另外一种写法[2]：

|AdvPRPE(A)−AdvPRFE(A)|≤q(q−1)2n+1(5)(5)|AdvEPRP(A)−AdvEPRF(A)|≤q(q−1)2n+1|\mathrm{Adv}_{E}^{PRP}(\mathcal{A})- \mathrm{Adv}_{E}^{PRF}(\mathcal{A})| \le \frac{q(q-1)}{2^{n+1}} \tag{5}
这两种形式均是正确的，使用时可根据上下文需求选择。可以看到， 式(4)表示敌手区分随机函数和随机置换的优势是一与询问次数qqq和nnn有关的值；当nnn取较大值如128时，这一上界q(q−1)2n+1q(q−1)2n+1\frac{q(q-1)}{2^{n+1}}变成为了可忽略的值，即当算法规模相对询问次数足够大时，敌手的区分能力将会很快减弱。

引理证明

为证明这一引理，我们定义事件 CollColl\mathrm{Coll} 为：当敌手AA\mathcal{A}提交不同的输出xi,xjxi,xjx_{i},x_{j}给寓言机OO\mathcal{O}后，OO\mathcal{O}返回了相同的输出yyy。而事件 DistDist\mathrm{Dist} 为CollColl\mathrm{Coll}的补集，即 Pr[Dist]=1−Pr[Coll]Pr[Dist]=1−Pr[Coll]\mathrm{Pr[Dist]}=1-\mathrm{Pr[Coll]}. 首先，我们说明这一结论：

Pr[Ap(⋅)(1n)=1]=PrAf(⋅)(1n)=1|Dist(6)Pr[Ap(⋅)(1n)=1]=Pr[Af(⋅)(1n)=1|Dist]\mathrm{Pr}[\mathcal{A}^{p(\cdot)}(1{n})=1] = \mathrm{Pr}[\mathcal{A}^{f(\cdot)}(1{n})=1 | \mathrm{Dist} ] \tag{6}
式(6)说明，当敌手的查询结果未发生碰撞时，敌手是无法区分一个随机函数和一个随机置换的。回顾PRF与PRP的定义，二者最大的区别就在于输入与输出所定义的概率空间不同。在PRP这种「置换」定义下，输入与输出为同一概率空间，这也就暗含了输入元素和输出元素必然为一一对应的双射关系；而在PRF这种「函数」定义下，输入与输出为不同空间，此时多个输入可能对应同一输出。

因此，如果已经先验地确定了输出不会发生碰撞，那么函数寓言机将「看起来」与置换寓言机完全一样，从而式(6)成立。这一结论的其他更严格的证明可参照xxx。

当式(6)成立时，令x=Pr[Ap(⋅)(1n)=1]=Pr[Af(⋅)(1n)=1|Dist]x=Pr[Ap(⋅)(1n)=1]=Pr[Af(⋅)(1n)=1|Dist]x=\mathrm{Pr}[\mathcal{A}^{p(\cdot)}(1{n})=1] = \mathrm{Pr}[\mathcal{A}^{f(\cdot)}(1{n})=1 | \mathrm{Dist} ]，令y=Pr[Af(⋅)(1n)=1|Coll]y=Pr[Af(⋅)(1n)=1|Coll]y=\mathrm{Pr}[\mathcal{A}^{f(\cdot)}(1{n})=1 | \mathrm{Coll}]，根据全概率公式，可得以下结论：

|Pr[Ap(⋅)(1n)=1]−Pr[Af(⋅)(1n)=1]|=∣∣x−Pr[Af(⋅)(1n)=1|Dist]Pr[Dist]−Pr[Af(⋅)(1n)=1|Coll]Pr[Coll]∣∣=|x−xPr[Dist]−yPr[Coll]|=|x−x+xPr[Coll]−yPr[Coll]|=|(x−y)Pr[Coll]|≤PrColl|Pr[Ap(⋅)(1n)=1]−Pr[Af(⋅)(1n)=1]|=|x−Pr[Af(⋅)(1n)=1|Dist]Pr[Dist]−Pr[Af(⋅)(1n)=1|Coll]Pr[Coll]|=|x−xPr[Dist]−yPr[Coll]|=|x−x+xPr[Coll]−yPr[Coll]|=|(x−y)Pr[Coll]|(7)≤Pr[Coll]\begin{align*}
|\mathrm{Pr}[\mathcal{A}^{p(\cdot)}(1{n})=1] - \mathrm{Pr}[\mathcal{A}^{f(\cdot)}(1{n})=1]|&=\left|x-\mathrm{Pr}[\mathcal{A}^{f(\cdot)}(1{n})=1|\mathrm{Dist}]\mathrm{Pr[Dist]}-\mathrm{Pr}[\mathcal{A}^{f(\cdot)}(1{n})=1|\mathrm{Coll}]\mathrm{Pr[Coll]}\right| \
&=|x-x\mathrm{Pr[Dist]}-y\mathrm{Pr[Coll]}|\
&=|x-x+x\mathrm{Pr[Coll]}-y\mathrm{Pr[Coll]}| \
&=|(x-y)\mathrm{Pr[Coll]}|\
&\le \mathrm{Pr[Coll]} \tag{7}
\end{align*}
式(7)的推导说明了此时敌手AA\mathcal{A}的区分能力不会超过 CollColl\mathrm{Coll} 事件的发生概率，也就意味着「除非让AA\mathcal{A}在不同的询问中获得了相同的结果，否则AA\mathcal{A}是不可能知道这是一个随机函数还是一个随机置换的」。这个结论在直觉上也是符合「函数」与「置换」的定义的。

因此，CollColl\mathrm{Coll} 事件若发生，则说明AA\mathcal{A}在提交的qqq次询问中，OO\mathcal{O}有两次选取了同一个yyy进行返回，由于函数模型下的OO\mathcal{O}是没有记忆性的（类似古典概型中的小球取出会放回），因此返回同一个yyy发生的概率是12n12n\frac{1}{2^{n}}。另一方面，qqq次询问一共会产生(q2)(q2)\binom{q}{2}个(xi,xj)(xi,xj)(x_{i}, x_{j})组合对。综上可知，Pr[Coll]≤(q2)12n=q(q−1)2n+1Pr[Coll]≤(q2)12n=q(q−1)2n+1\mathrm{Pr[Coll]}\le \binom{q}{2}\frac{1}{2^{{n}}=\frac{q(q-1)}{2}{n+1}}. 证毕。

不同的界

其实，在许多地方，式(4)(5)的不等式上界会写为q22n+1q22n+1\frac{q^{2}}{2{n+1}}，即为[3]：

|AdvPRPE(A)−AdvPRFE(A)|≤|Pr[Af(⋅)(1n)=1]−Pr[Ap(⋅)(1n)=1]|≤q22n+1(8)(8)|AdvEPRP(A)−AdvEPRF(A)|≤|Pr[Af(⋅)(1n)=1]−Pr[Ap(⋅)(1n)=1]|≤q22n+1|\mathrm{Adv}_{E}^{PRP}(\mathcal{A})- \mathrm{Adv}_{E}^{PRF}(\mathcal{A})| \le |\mathrm{Pr}[\mathcal{A}^{f(\cdot)}(1{n})=1] - \mathrm{Pr}[\mathcal{A}^{p(\cdot)}(1{n})=1]| \le \frac{q^{2}}{2{n+1}} \tag{8}
由先前的证明过程可知，上界q(q−1)2n+1q(q−1)2n+1\frac{q(q-1)}{2^{{n+1}}若能成立，则自然蕴含q22n+1q22n+1\frac{q}{2}}{2^{n+1}}也是成立的。因此两种版本的引理公式均是正确的。在许多论文中，式(8)其实是更常见的写法，这是因为平方式的形式更利于表达和记忆。两种上界之所以能共存，是由于前者更严密（tight），后者更好记，在使用时按需选择即可。

关于这一不同的上界，更多信息可以参见这一解答

总结

PRP/PRF转换引理其实只是许多复杂证明的第一步，但其「只要没碰撞，敌手就分不出来」这一核心思想在对称算法的证明中却十分重要。该引理说明了如果一个加密算法是PRP，那它必然也是一个PRF，这一基础推论应能在证明中灵活应用。此外，如果见到上界不同的两个引理版本，请不要惊慌，两个版本都是正确的，可按需使用。最后，本文的所有重点总结如下：

• PRF与PRP的定义和性质
• 不可区分性的本质
• PRP/PRF转换引理内容
• 碰撞事件的内涵及其概率计算

感谢你的阅读，欢迎给出建议，以一句歌词作为结束。

“劳斯难面对，却跟她勾过手指；莱斯，偏偏那样痴” —— 黄伟文《劳斯·莱斯》

参考

[1] https://eprint.iacr.org/2004/331.pdf
[2] https://crypto.stanford.edu/~dabo/cs255/lectures/PRP-PRF.pdf
[3] https://crypto.stanford.edu/~dabo/cryptobook/BonehShoup_0_5.pdf