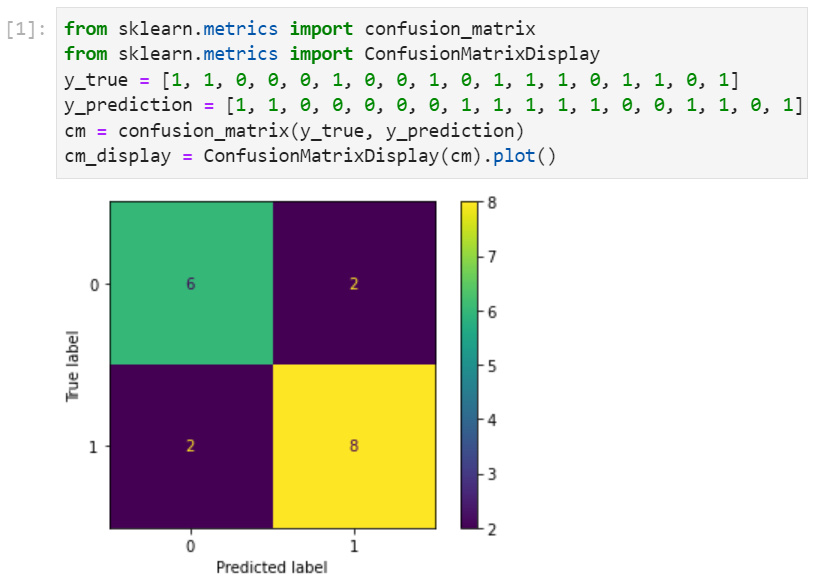
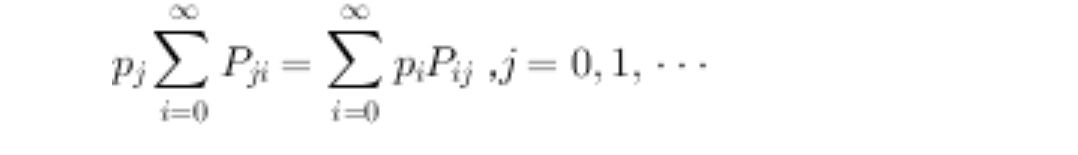SNTP(Simple Network Time Protocal简单网络时间协议),用于跨广域网或局域网同步时间的协议,具有较高的精确度(几十毫秒)。SNTP是NTP协议的简化版,两者分别在RFC1305和RFC2030介绍。
SNTP工作方式
SNTP采用客户端/服务器的工作方式,可以采用单播或者广播的模式。
单播即客户端定期直接与SNTP服务器交互获取时间差进行校时。
广播则是SNTP服务器定期向指定的多播地址发送时间信息,SNTP客户端通过监听这些多播地址来获取时间信息进行同步。UNIX网络编程中有SNTP广播方式的部分实现代码。
SNTP校时原理
SNTP协议主要是通过记录客户端向服务器发送数据包时的时间戳t1,服务器端接收到该数据包时的时间戳t2,服务器向客户端回应时的时间戳t3和最后客户端接收到服务器回应时的时间戳t4来计算客户端时间和服务器端时间的偏差,从而进行校时操作,如下图所示。
则t1与t2之间的时间差为((T2-T1)+ (T3-T4))/2
数据包在网络上的传播时间是 (T2-T1) + (T4-T3)
知识点
1、NTP时间戳从1900年开始记秒数,而UNIX时间戳从1970年开始记秒数,即记录到NTP结构体中的时间要加上JAN_1970(1900到1970共70年的秒数),而从起获取出来需减掉JAN_1970
2、
/* Offset between struct timeval.tv_sec anda tai64_t */
#define NTPLEAPS_OFFSET (4611686018427387914ULL)/* Hide this ugly value from programmes */
#define SEC_TO_TAI64(s) (NTPLEAPS_OFFSET + (u_int64_t)(s))
#define TAI64_TO_SEC(t) ((t) - NTPLEAPS_OFFSET)对于这部分我还没搞清楚,如有明白的麻烦跟我讲解下,如NTPLEAPS_OFFSET是怎么来的?
为啥要做这样的转换?
校时操作
获取时间差后就是进行本地校时操作。Linux系统分系统时间和RTC时间,如果只修改了系统时间,那么设备重启后并不时校时后正常运行的时间。如果修改了RTC时间,则重启后是校时后正常运行的时间。这两者的区别如下所述。
RTC(Real Time Clock)时间有一套独立的计时系统,是设备上由电池供电的硬件时钟。和设备状态无关,即使设备关机,RTC时间仍然在运行,是设备的标准时间,无夏令时和冬令时的区分,只有设置时间的时候才能修改,为UTC时间。
系统时间(System Clock),即设备当前时间,使用操作系统自带的晶振进行计时,在设备关机的时候将会清空,设备重启时会获取设备RTC时间来重新设置系统时间,之后独立于RTC时间运行。有夏令时,在没有开启夏令时的情况下,和设备RTC时间基本同步。
设备存在系统时间和RTC时间好处如只想临时修改下当前时间,则只需要修改下系统时间即可,过后想修改回原有时间,则只需同步下RTC时间便可。