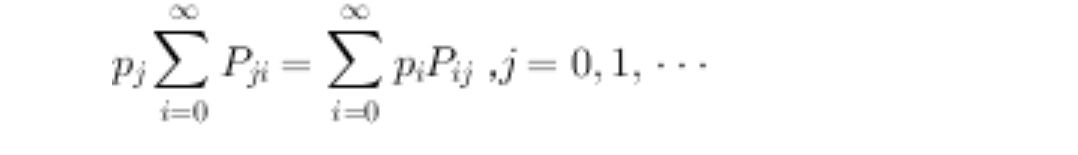公众号关注 52DATA ,获得更多数据分析知识,感谢支持—>
文章目录
- 马尔可夫过程
- 1. 马尔可夫性
- 2. 马尔可夫链
- 2.1 转移概率矩阵(随机矩阵)
- 2.2 状态概率
- 2.3 平稳分布
- 3.一个很经典的例题帮助理解马尔科夫预测方法
- 1.求状态转移概率
- 2.运用状态概率进行预测
- 3.准备使用1950-1979年的数据来预测1979-1989的数据
马尔可夫过程
马尔可夫过程(Markov process)是一类随机过程。它的原始模型马尔可夫链,由俄国数学家A.A.马尔可夫于1907年提出。马尔可夫过程是研究离散事件动态系统状态空间的重要方法,它的数学基础是随机过程理论。
N阶马尔可夫过程:每个状态依赖于前N个状态
1阶马尔可夫过程:最简单的马尔可夫过程,只与前一个状态有关
1. 马尔可夫性
系统的下一个状态S(t+1)仅仅与当前状态S(t)有关,与之前状态无关
公式表示
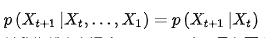
此性质称为马尔可夫性,亦称无后效性或无记忆性
若随机过程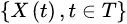
满足马尔可夫性,则称为马尔可夫过程
当然 二阶马尔科夫就是:系统的下一个状态S(t+1)仅仅与前两个状态有关S(t),S(t-1)
三阶马尔科夫就是:系统的下一个状态S(t+1)仅仅与前三个状态有关S(t),S(t-1),S(t-2)
2. 马尔可夫链
2.1 转移概率矩阵(随机矩阵)
若马尔可夫链在时刻 ( t − 1 ) 处于状态 j,在时刻 t移动到状态 i,将转移概率记作
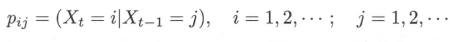
其中
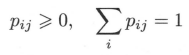
则可以构成马尔可夫链的转移概率矩阵

例如

这个马尔科夫链是表示股市模型的,共有三种状态:牛市(Bull market), 熊市(Bear market)和横盘(Stagnant market)。每一个状态都以一定的概率转化到下一个状态。比如,牛市(Bull market)以0.025的概率转化到横盘(Stagnant market)的状态。这个状态概率转化图可以以矩阵的形式表示。如果我们定义矩阵阵P某一位置P(i,j)的值为P(j|i),即从状态i转化到状态j的概率,并定义牛市为状态0, 熊市为状态1, 横盘为状态2. 这样我们得到了马尔科夫链模型的状态转移矩阵为
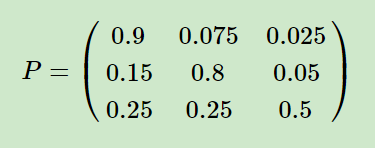
每一行的值为1,一个状态向外的状态的概率之和1
2.2 状态概率
考虑马尔可夫链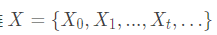
在时刻t的概率分布,称为时刻 t 的状态分布 或 状态向量 (state vector)或 状态概率,记作
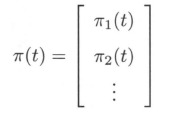
其中,
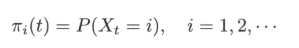
通常初始分布 π(0) 的向量只有一个分量是1,其余分量都是0,表示马尔可夫链从一个具体状态开始
马尔可夫链 X在时刻t的状态分布,可以由在时刻(t−1) 的状态分布以及转移概率分布决定
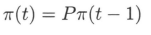
递推可得
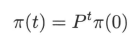

上式说明,马尔可夫链的状态分布由初始分布和转移概率分布决定
2.3 平稳分布
若干个时间步后收敛于平稳分布

3.一个很经典的例题帮助理解马尔科夫预测方法
有一张某地区农业收成变化表,有三个状态,即“丰收”、“平收”和“欠收”。记E1为“丰收”状态,E2为“平收”状态,E3为“欠收”状态,如下表:

1.求状态转移概率
补充知识,条件概率
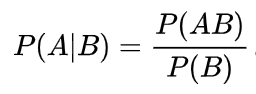
在15个从E1出发(转移出去)的状态转移中,有3个是从E1转移到E1的(即1→2,24→25,34→35),有7个是从E1转移到E2的(即2→3,9→10,12→13,15→16,29→30,35→36,39→40),有5个是从E1转移到E3的(即6→7,17→18,20→21,25→26,31→32)
P11=P(E1->E1)=P(E1|E1)=3/15 0.2
P12=P(E1->E2)=P(E1|E2)=7/15 0.4666666666666667
P13=P(E1->E3)=P(E1|E3)=5/15 0.3333333333333333
同理求出:
P21=P(E2->E1)=P(E2|E1)=7/13= 0.5384615384615384
P22=P(E2->E2)=P(E2|E2)=2/13= 0.15384615384615385
P23=P(E2->E3)=P(E2|E3)=4/13= 0.3076923076923077
P31=P(E3->E1)=P(E3|E1)=4/11= 0.36363636363636365
P32=P(E3->E2)=P(E3|E2)=5/11= 0.45454545454545453
P33=P(E3->E3)=P(E3|E3)=2/11= 0.18181818181818182
所以,该地区农业收成变化的状态转移概率矩阵为(保留三位小数)

2.运用状态概率进行预测
基本原理见上方
如果将1989年的农业收成状态记为π(0)=[0,1,0](因为1989年处于“平收”状态),
带入
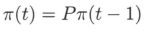
就可以求得1990—2007年可能出现的各种状态的概率
1990年状态概率为[0.53846154 0.15384615 0.30769231]
1991年状态概率为[0.30242066 0.41481083 0.28276851]
1992年状态概率为[0.38666872 0.33347783 0.27985344]
1993年状态概率为[0.35866362 0.3589558 0.28238058]
1994年状态概率为[0.36770046 0.35095514 0.2813444 ]
1995年状态概率为[0.36482299 0.35347047 0.28170654]
1996年状态概率为[0.36573359 0.35267923 0.28158718]
1997年状态概率为[0.36544626 0.35292819 0.28162555]
1998年状态概率为[0.3655368 0.35284985 0.28161335]
1999年状态概率为[0.36550829 0.3528745 0.28161721]
2000年状态概率为[0.36551726 0.35286674 0.28161599]
2001年状态概率为[0.36551444 0.35286918 0.28161638]
2002年状态概率为[0.36551533 0.35286842 0.28161626]
2003年状态概率为[0.36551505 0.35286866 0.2816163 ]
2004年状态概率为[0.36551514 0.35286858 0.28161628]
2005年状态概率为[0.36551511 0.35286861 0.28161629]
2006年状态概率为[0.36551512 0.3528686 0.28161629]
2007年状态概率为[0.36551511 0.3528686 0.28161629]
2008年状态概率为[0.36551511 0.3528686 0.28161629]
2009年状态概率为[0.36551511 0.3528686 0.28161629]
可以看到从2007年开始,状态概率就达到平衡了,经过无穷多次状态转移后所得到的状态概率称为终极状态概率,或称平衡状态概率。
数学表示:存在平衡状态概率一个 π,使得π=πP ,则 π 是平衡状态概率。

即

求解π1,π2,π3即可
平衡状态概率是用来预测马尔可夫过程在遥远的未来会出现什么趋势的重要信息。
3.准备使用1950-1979年的数据来预测1979-1989的数据
直接上代码
#1950--1979年数据
data=["E1","E1","E2","E3","E2","E1","E3","E2","E1","E2",
"E3","E1","E2","E3","E1","E2","E1","E3","E3","E1",
"E3","E3","E2","E1","E1","E3","E2","E2","E1","E2",
]#1979-1989年数据
data1=["E1","E3","E2","E1","E1","E2","E2","E3","E1","E2"]E1data=[]#计算从E1开始的状态
for i in range(len(data)-1):if data[i]=="E1":E1data.append(data[i+1])
E2data=[]#计算从E2开始的状态
for i in range(len(data)-1):if data[i]=="E2":E2data.append(data[i+1])E3data=[]#计算从E3开始的状态
for i in range(len(data)-1):if data[i]=="E3":E3data.append(data[i+1])E1E1=0#E1->E1个数
E1E2=0#E1->E2个数
E1E3=0#E1->E3个数
for i in range(len(E1data)):if E1data[i]=="E1":E1E1=E1E1+1if E1data[i]=="E2":E1E2=E1E2+1if E1data[i]=="E3":E1E3=E1E3+1p11=E1E1/len(E1data)
p12=E1E2/len(E1data)
p13=E1E3/len(E1data)
print("p11=",p11)
print("p12=",p12)
print("p13=",p13)E2E1=0#E2->E1个数
E2E2=0#E2->E2个数
E2E3=0#E2->E3个数
for i in range(len(E2data)):if E2data[i]=="E1":E2E1=E2E1+1if E2data[i]=="E2":E2E2=E2E2+1if E2data[i]=="E3":E2E3=E2E3+1p21=E2E1/len(E2data)
p22=E2E2/len(E2data)
p23=E2E3/len(E2data)
print("p21=",p21)
print("p22=",p22)
print("p23=",p23)E3E1=0#E3>E1个数
E3E2=0#E3->E2个数
E3E3=0#E3->E3个数
for i in range(len(E3data)):if E3data[i]=="E1":E3E1=E3E1+1if E3data[i]=="E2":E3E2=E3E2+1if E3data[i]=="E3":E3E3=E3E3+1p31=E3E1/len(E3data)
p32=E3E2/len(E3data)
p33=E3E3/len(E3data)
print("p31=",p31)
print("p32=",p32)
print("p33=",p33)import numpy as np
P=np.array([[p11,p12,p13],[p21,p22,p23],[p31,p32,p33]])
#注意numpy的数字是int32 会截取数据
P#状态转移概率# 因为1979年的状态是E2,所以假设pai1979=[0,1,0]
pai1979=np.array([0,1,0])
pai1980=pai1979.dot(P)pai1980
#可以看出1980的E1概率比较大 array([0.55555556, 0.11111111, 0.33333333])pai1981=pai1980.dot(P)
pai1981
#可以看出1981的E2概率比较大,但与事实相反 array([0.27384961, 0.41301908, 0.31313131])pai=np.array([0,1,0])
for i in range(10):pai=pai.dot(P)print("%s年=%s,预测状态为E%s"%(1980+i,pai,list(pai).index(max(list(pai) ))+1))1980年=[0.55555556 0.11111111 0.33333333],预测状态为E1
1981年=[0.27384961 0.41301908 0.31313131],预测状态为E2
1982年=[0.38362299 0.30953758 0.30683944],预测状态为E1
1983年=[0.34399477 0.34514023 0.310865 ],预测状态为E2
1984年=[0.35791074 0.33287239 0.30921686],预测状态为E1
1985年=[0.35307608 0.33710224 0.30982168],预测状态为E1
1986年=[0.35474857 0.33564346 0.30960798],预测状态为E1
1987年=[0.35417099 0.33614661 0.3096824 ],预测状态为E1
1988年=[0.35437031 0.33597306 0.30965663],预测状态为E1
1989年=[0.35430154 0.33603292 0.30966554],预测状态为E1
#1979-1989年数据
data1=["E1","E3","E2","E1","E1","E2","E2","E3","E1","E2"]#预测的结果
yucedata=["E1","E2","E1","E2","E1","E1","E1","E1","E1","E1"]
xt=0#相同个数for i in range(len(data1)):if data1[i]==yucedata[i]:xt=xt+1
xt/len(data1) #正确率只有0.3的准确率(数据量太小)
公众号关注 52DATA ,获得更多数据分析知识,感谢支持—>