前言

LCS可以描述两段文字之间的“相似度”，即它们的雷同程度，从而能够用来辨别抄袭。另一方面，对一段文字进行修改之后，计算改动前后文字的最长公共子序列，将除此子序列外的部分提取出来，这种方法判断修改的部分，往往十分准确。

算法介绍

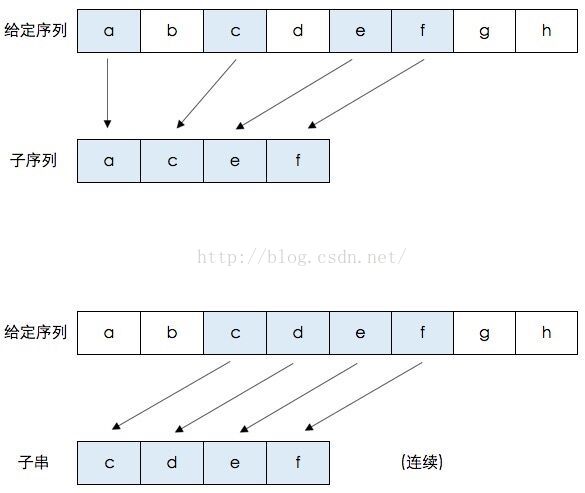
子序列：一个序列S任意删除若干个字符得到新序列T。

公共子序列：两个序列X和Y中都存在的项组成的序列。

最长公共子序列：两个序列X和Y的公共子序列中最长的序列。

例如：

字符串13455与245576的最长公共子序列为455

字符串acdfg与adfc的最长公共子序列为adf

求取算法详解

第一种：自定义暴力求取方式

假定字符串X，Y的长度分别为m，n

X的一个子序列即下标序列{1, 2, …, m}的严格递增子序列，因此，X共有2m个不同子序列；同理，Y有2n个不同子序列，从而穷举搜索法需要指数时间O(2m*2n)；

对X的每一个子序列，检查它是否也是Y的子序列，从而确定它是否为X和Y的公共子序列，并且在检查过程中选出最长的公共子序列；

显然，不可取。

针对该种算法进行改良，只对第一组数据进行依次列出，然后与第二组进行比较。其时间复杂度虽然也很高，但与2m*2n相比还是要少一些。

void lscChangeViolence(int *X, int *Y, int m) {int *AllX, *AllFlag, *result;AllX = (int*)malloc(sizeof(int)*m);AllFlag = (int*)malloc(sizeof(int)*m);result = (int*)malloc(sizeof(int)*m);for (int i = 0; i < m; i++) {AllX[i] = 0;AllFlag[i] = 0;result[i] = -1000;}int count = 1;while (count < pow(2, m)) {int num = 0;// 按照取某一位的值和不取某一位的值，将X中的某些值赋值给AllXfor (int i = 0; i < m; i++) {			if (((count >> i) & 1) == 1) {AllX[num] = X[i];num++;}}// 给定比较数组int *compare;compare = (int*)malloc(sizeof(int)*(num));for (int i = 0; i < num; i++) {compare[i] = AllX[i];}int comNum = 0;int jump = 0;int maxNum = -1;int start = 0;// 如果子数组与第二组匹配上，则记录长度，并记下数据for (int i = 0; i < num; i++) {if (start > n) {break;}for (int j = start; j < n; j++) {if (compare[i] == Y[j]) {start = j + 1;comNum++;break;}}if (comNum == i) {break;}}if (comNum > maxNum) {maxNum = comNum;for (int k = 0; k < maxNum; k++) {result[k] = compare[k];}}count++;}for (int i = 0; i < 5; i++) {if (result[i] != -1000) {printf("result[%d]=%d\n", i, result[i]);}}
}

第二种：动态规划法

字符串X，长度为m，从1开始数；

字符串Y，长度为n ，从1开始数；

LCS(X , Y) 为字符串X和Y的最长公共子序列。

若xm=yn(最后一个字符相同)，则：Xm与Yn的最长公共子序列Zk的最后一个字符必定为xm或yn。

LCS(Xm , Yn) = LCS(Xm-1 , Yn-1) + xm

若xm≠yn，则：要么LCS(Xm,Yn)=LCS(Xm-1, Yn)，要么LCS(Xm,Yn)=LCS(Xm, Yn-1)。

则：

$LCS(X_{m},Y_{n})=\left\{\begin{matrix}LCS(X_{m-1},Y_{n-1}) \\ max\left \{ LCS(X_{m-1},Y_{n}),LCS(X_{m},Y_{n-1}) \right \} \end{matrix}\right.\begin{matrix} x_{m}=y_{n} \\ x_{m}\neq y_{n} \end{matrix}$

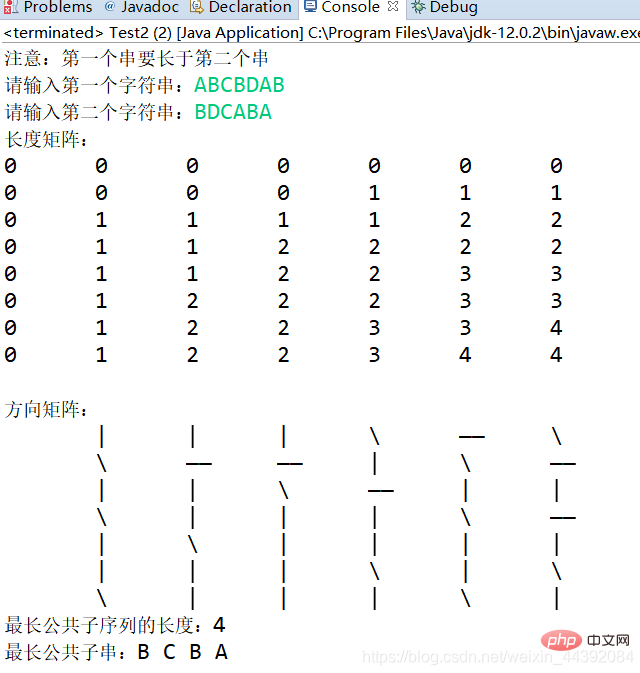
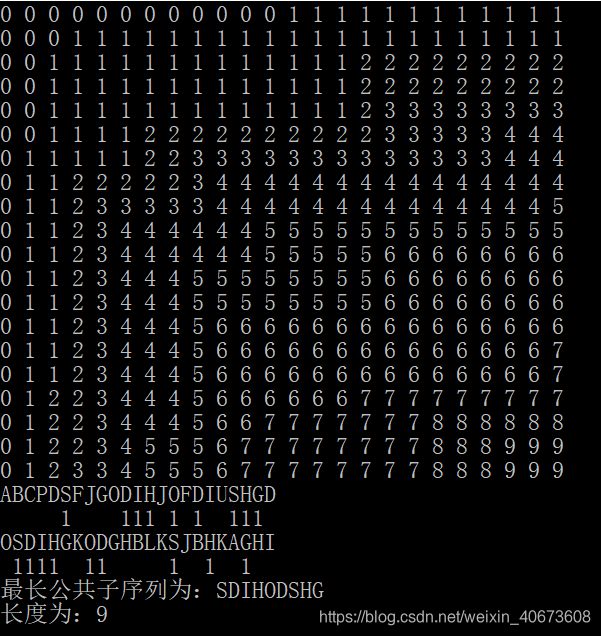
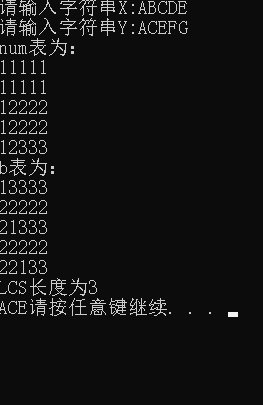
使用二维数组C[m,n]。

c[i,j]记录序列Xi和Yj的最长公共子序列的长度。

当i=0或j=0时，空序列是Xi和Yj的最长公共子序列，故c[i,j]=0。

$c(i,j)=\left\{\begin{matrix} 0\\ c(i-1,j-1)\\ max\left \{ c(i-1,j),c(i,j-1)) \right \} \end{matrix}\right.\begin{matrix} i=0,j=0\\ i>0,j>0,x_{i}=y_{j}\\ i>0,j>=0,x_{i}\neq y_{j} \end{matrix}$

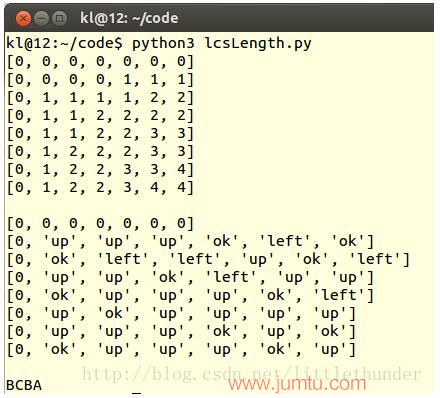
使用二维数据B[m,n]，其中，b[i,j]标记c[i,j]的值是由哪一个子问题的解达到的。即c[i,j]是由c[i-1,j-1]+1或者c[i-1,j]或者c[i,j-1]的哪一个得到的。取值范围为Left，Top，LeftTop三种情况。

// 根据规则将c[i][j]进行赋值，获取方向数组b[i][j]
void lcs_length(char *X, char *Y, int mLength, int nLength,int **C,char **B) {int num = 0;for (int i = 1; i < mLength + 1; i++) {for (int j = 1; j < nLength + 1; j++) {if (X[i-1] == Y[j-1]) {C[i][j] = C[i - 1][j - 1] + 1;B[i][j] = 'x';}else if (C[i - 1][j] >= C[i][j - 1]) {C[i][j] = C[i - 1][j];B[i][j] = 's';}else {C[i][j] = C[i][j - 1];B[i][j] = 'z';}}}for (int i = 0; i < mLength + 1; i++) {for (int j = 0; j < nLength + 1; j++) {printf("C[%d][%d]=%d  ", i, j, C[i][j]);}printf("\n");}}

下面打印最长公共子序列

// 从最后的位置进行索引，按照方向依次寻找数据，将标记为x的数据打印即为最长子数组
void lcsPrint(char **B, char *X, int i, int j) {if (i == 0 || j == 0) {return;}if (B[i][j] == 'x') {lcsPrint(B, X, i - 1, j - 1);printf("X[%d]=%c\n", i - 1, X[i - 1]);}else if (B[i][j] == 's') {lcsPrint(B, X, i - 1, j);}else {lcsPrint(B, X, i, j - 1);}
}